Готовые РГР / Расчетно-графическая работа Вариант 6

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский

технический университет им. А.Н. Туполева-КАИ»

(КНИТУ-КАИ)

Институт Радиоэлектроники и телекоммуникаций

(наименование института (факультета), филиала)

Кафедра радиофотоники и микроволновых технологий (РФМТ)

(наименование кафедры)

11.03.01 Радиотехника

(шифр и наименование направления подготовки (специальности))

Расчетно-графическая работа (РГР)

по дисциплине: «Цифровая обработка сигналов»

(6 вариант)

Обучающийся

(номер группы) (Ф.И.О.)

Руководитель Доцент

(должность) (Ф.И.О.)

Казань 2020

Задание № 1

Исходные данные: Вариант 6

Х1=1

Х2=0,5

Х3=0

φ1=0

φ2=

φ3=0

F1=2МГц

Fд=16МГц

Δt=1/512мкс

1.Сформировать аналоговый сигнал в виде суммы трех гармонических колебаний

где

F₂ =2 F₁, F₃ = 3 F₁.

2. Определить амплитудный спектр аналогового сигнала.

3. Сформировать вспомогательный сигнал в виде периодической последовательности единичных отсчетов с периодом, равным интервалу дискретизации

4. Сформировать дискретный сигнал .

5. Определить амплитудные спектры аналогового и дискретного сигналов и убедиться в том, что при дискретизации имеет место эффект размножения спектра аналогового сигнала.

6. Восстановить аналоговый сигнал из дискретного путем выделения из спектра дискретного сигнала той части, которая соответствует спектру аналогового сигнала. Сравнить восстановленный сигнал с исходным аналоговым сигналом.

7. Повторить машинный эксперимент при в два раза меньшей частоте дискретизации.

Для моделирования аналогового сигнала преобразуем соотношение (1), определив количество расчетных точек i_s в периоде T₁ аналогового сигнала

=216

Сигнал в расчетной точке i определяется следующим образом:

где

Количество расчетных точек в интервале дискретизации равно =32

Дискретный сигнал определяется следующим соотношением

Расчет частот спектральных составляющих дискретного сигнала по формуле

k = 0

1. F=F₁, f₁ = F₁ = 2 МГц,

2. F=F₂, f₂ = F₂ = 4 МГц.

K=1

3. F=F₂, f₄ = F_d – F₂ = 16 – 4 = 12 МГц,

4. F=F₁, f₆ = F_d – F₁ = 16 – 2 = 14 МГц,

5. F=F₁, f₇ = F_d + F₁ = 16 + 2 = 18 МГц,

6. F=F₂, f₉ = F_d + F₂ = 16 + 4 = 20 МГц.

Результат моделирования по программе «Diskret» при исходных данных в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 1.

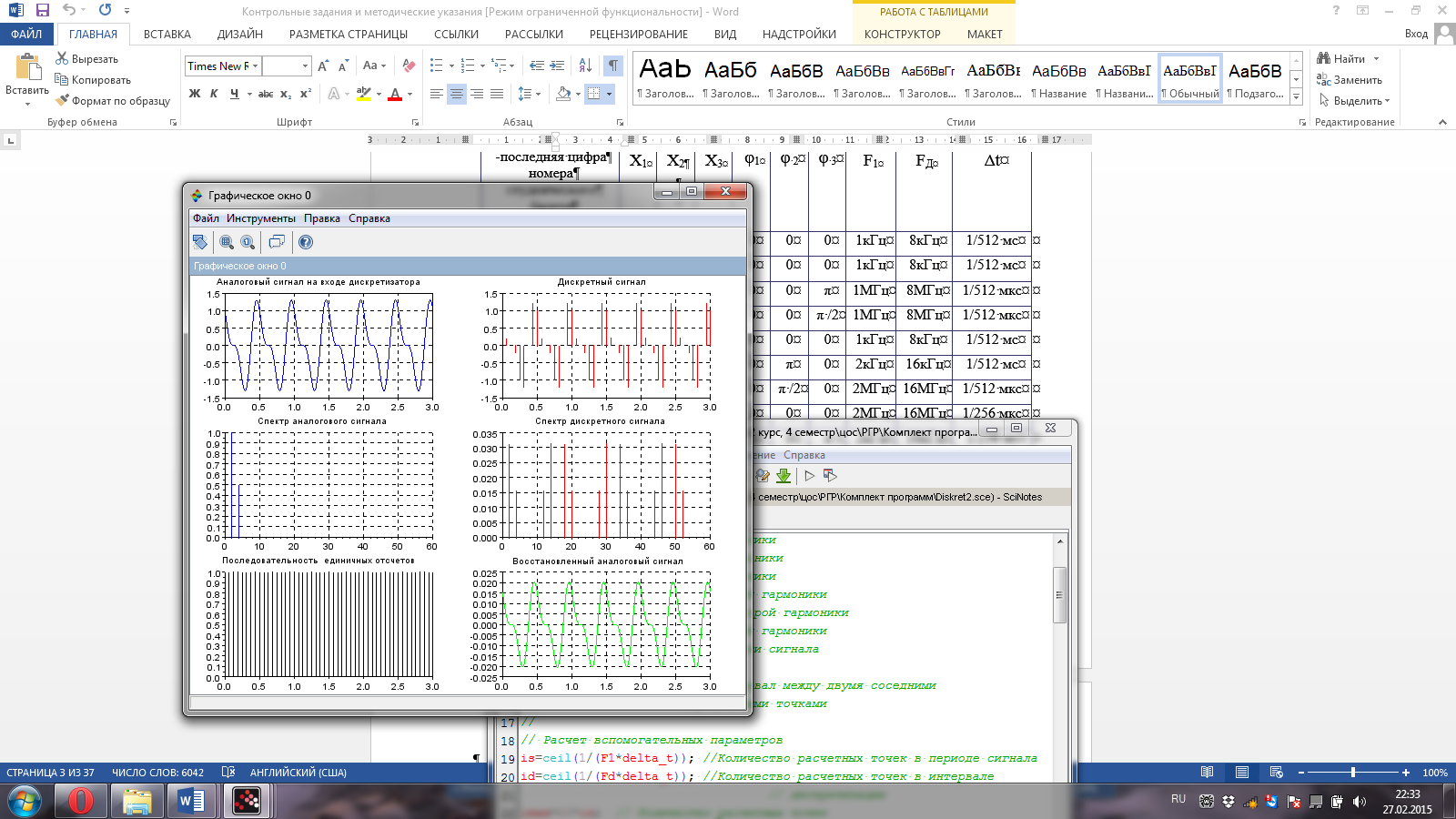
Рис.1 Временные и спектральные диаграммы при F_Д > 2F₃

Выводы:

• В спектре аналогового сигнала присутствуют 2 гармоники, соответствующие сигналам x1(t) и x2(t), так как амплитуда сигнала х3(t)=0. Частоты спектральных составляющих соответствуют f1=2МГц и f2=4МГц. В спектре дискретного сигнала присутствуют спектральные составляющие на исходных частотах f1=2МГц и f2=4МГц, а также наблюдается появление составляющих на частотах, отстоящих с двух сторон от fd=16МГц на 2 и 4 МГц соответственно. Таким образом полученные расчеты соответствуют рассчитанным значениям. В спектре дискретного сигнала наблюдается эффект размножения спектра.

• Восстановленный аналоговый сигнал повторяет форму исходного.

Расчет частот спектральных составляющих дискретного сигнала при F_Д=8МГц< 2F₃

k = 0

7. F=F₁, f₁ = F₁ = 2 МГц,

8. F=F₂, f₂ = F₂ = 4 МГц.

K=1

9. F=F₂, f₄ = F_d – F₂ = 8 – 4 = 4 МГц,

10. F=F₁, f₆ = F_d – F₁ = 8 – 2 = 6 МГц,

11. F=F₁, f₇ = F_d + F₁ = 8 + 2 = 10 МГц,

12. F=F₂, f₉ = F_d + F₂ = 8 + 4 = 12 МГц.

Результат моделирования по программе «Diskret» при исходных данных в виде временных и спектральных диаграмм аналогового и дискретного сигнала приведён на рисунке 2

Рис.2 Временные и спектральные диаграммы при F_Д < 2F₃

Выводы:

• При Fд=8 МГц не выполняется условие Fд>2Fв. Следовательно аналоговый сигнал не может быть восстановлен без искажений. Также наблюдается наложение спектральных составляющих в спектре дискретного сигнала.

• Восстановленный аналоговый сигнал сильно искажен по сравнению с исходным.

Задание №2

Требуется определить системную функцию H(z), комплексный коэффициент передачи K(jθ), АЧХ K(f_N) и ФЧХ φ(f_N) цифрового фильтра, где θ = 2π f_N, f_N=f/F_Д – нормированная частота.

Построить графики АЧХ и ФЧХ

Коэффициенты системной функции фильтра B=-1

рис. 3 Графическое представление алгоритма функционирования фильтра

Из рисунка видно, что

y_n=B*x_n+x_n-4

Воспользовавшись свойствами Z-преобразования, перейдем от разностных уравнений к уравнениям для Z-преобразований дискретных сигналов

Y(z)=B*X(z)+X(z)*z^-4

Разделив Y(z) на X(z), получим системную функцию цифрового фильтра

Для нахождения комплексного коэффициента передачи фильтра подставим в выражение системной функции , где j – мнимая единица, - нормированная частота

Определим АЧХ фильтра

или

Определим ФЧХ фильтра

Рис. 4 АЧХ и ФЧХ фильтра

Задание 3

Требуется выполнить синтез цифрового фильтра с линейной ФЧХ и АЧХ, выражаемой функцией Гаусса.

fNg	σ	δm	n0	Xp	fNp
0.05	2	-60	15	2	0.15

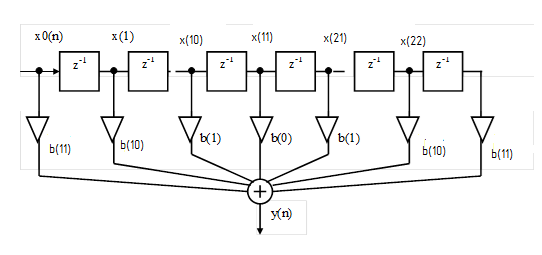
Рис.5 Нерекурсивный фильтр с линейной ФЧХ

Синтез фильтра выполнен по программе «FilterGauss». sce.

Результаты синтеза:

Половина длины линии задержки фильтра K0=11.

Коэффициенты системной функции приведены в таблице

Коэффициенты системной функции фильтра

Номер коэффициента k	Значение коэффициента b(k)
0	0,12
1	0,058
2	0,05
3	0,04
4	0,029
5	0,019
6	0,012
7	6,5*10-3
8	3,26*10-3
9	1,5*10-3
10	0.7*10-3
11	0.2*10-3

АЧХ фильтра определяется следующим соотношением:

.

ФЧХ фильтра без приведения в интервал от – π до π , определяется соотношением

.

В двух последних соотношениях K0=11

Рис.6 АЧХ и ФЧХ при К0=11

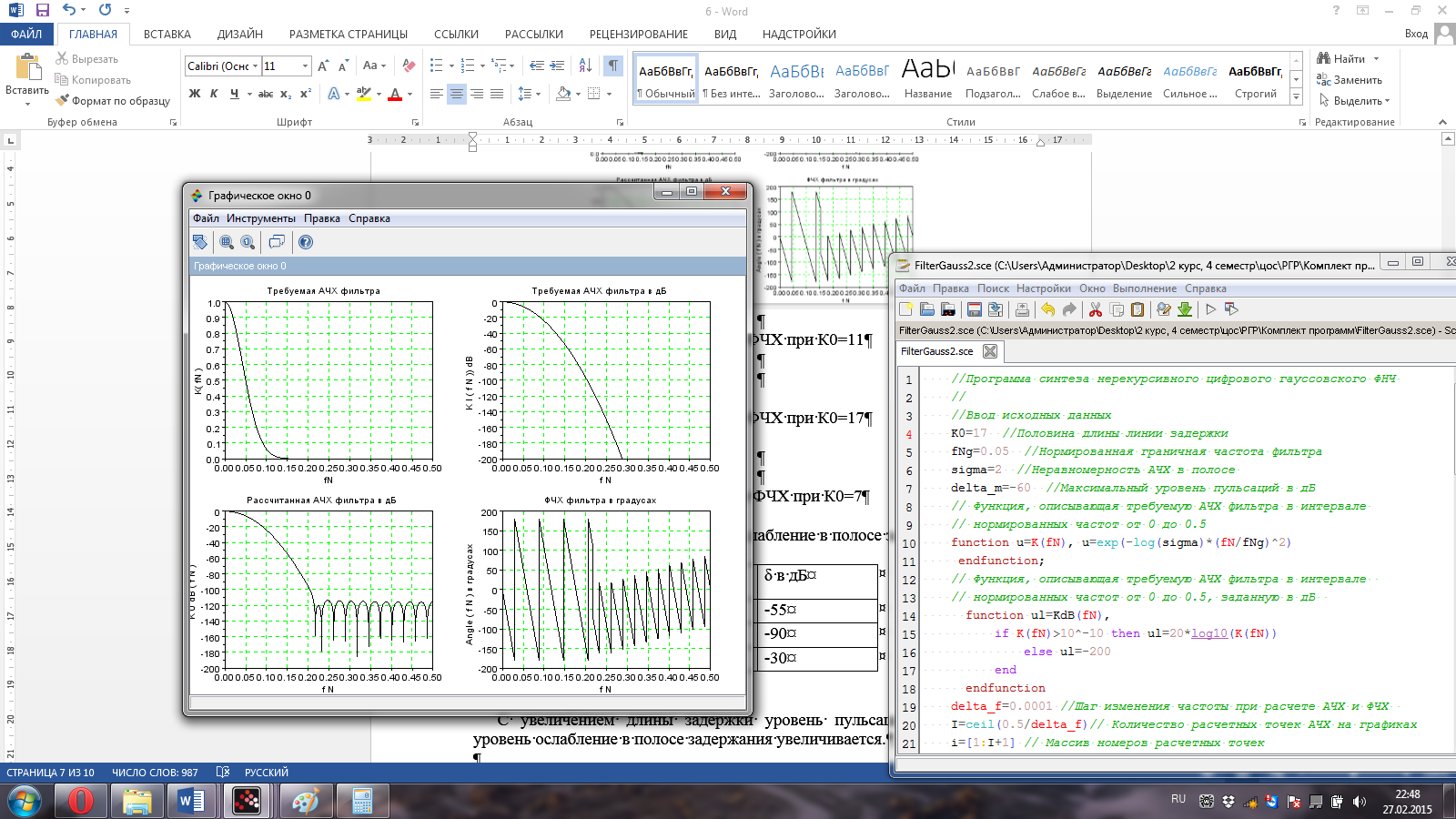
Рис.7 АЧХ и ФЧХ при К0=17

Рис. 8 АЧХ и ФЧХ при К0=7

Влияние длины линии задержки на ослабление в полосе задерживания

K0	δ в дБ
11	-60
17	-110
7	-30

Выводы:

С увеличением длины задержки уровень пульсаций уменьшается, а уровень ослабление в полосе задержания увеличивается.

При моделировании процесса фильтрации на вход фильтра подаётся сумма сигнала и помехи x0(n).

Полезный сигнал представляет собой случайную последовательность прямоугольных элементарных посылок xc с уровнями 1 и -1 , формирование которых представлено на рисунке .

Рис.9 Формирование сигнала на входе фильтра

Формирование элементарных по ссылок осуществляется с использованием счетчика отсчетов. Переменная счетчика z изменяется в соответствии с соотношением

В момент дискретного времени, когда переменная счетчика равна нулю, определяется знак элементарной посылки в зависимости от значения случайной величины .

Если формируется посылка позитива xc = 1, в противном случае формируется посылка негатива xc = -1. Значение xc, определённое при z = 0, остаётся неизменным до следующего нулевого значения z.

Помеха определяется соотношением:

где Xp – амплитуда помехи, fNp – нормированная частота помехи.

Моделирование осуществляется с использованием следующих соотношений:

Определение выходного сигнала

Сдвиг сигнала в линии задержки

x(2K0)=x(2K0-1), x(2K0-1)=x(2K0-2), .. x(K0)=x(K0-1), .. x(2)=x(1), x(1)=x0(n),

где K0=11.

Результатом моделирования являются следующие временные диаграммы.

Рис.10 Результат моделирования

Вывод: в результате моделирования мы увидели, что фильтр не пропускает помеху, при этом полезный сигнал получается на выходе фильтра без искажений. Однако не без потерь, как мы видим, уменьшилась крутизна сигнала, и появились небольшие пульсации.

Список использованной литературы

аналоговый сигнал дискретный цифровой

1. Методическое письмо, Самигуллин Р.Р.

2. Цифровая обработка сигнала и сигнальные процессоры, Иванова В.Г., Тяжев А.И. (Самара 2008 г.)

Размещено на Allbest.ru

12