Графы4

Цель работы: реализовать и проверить на тестовом примере специальный алгоритм на графе.

Индивидуальный вариант:

Вариант № 21 (1).

На рисунке 1 представлен специальный алгоритм согласно индивидуальному варианту.

Рисунок 1- Специальный алгоритм

Ход работы

Реализован взвешенный неориентированный полносвязный граф (Рисунок 2).

Листинг 1. Создание матрицы смежности и визуализация графа

import numpy as np

import networkx as nx

import matplotlib.pyplot as plt

N = 10

adj_matrix = np.random.randint(1, 10, size=(N, N))

np.fill_diagonal(adj_matrix, 0)

print("Матрица смежности графа:")

print(adj_matrix)

G = nx.from_numpy_array(adj_matrix)

plt.figure(figsize=(9, 9))

pos = nx.circular_layout(G)

nx.draw(G, pos, with_labels=True, node_size=300, node_color='lightblue', font_size=10)

edge_labels = {(i, j): adj_matrix[i][j] for i in range(N) for j in range(N) if adj_matrix[i][j] != 0}

nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

plt.show()

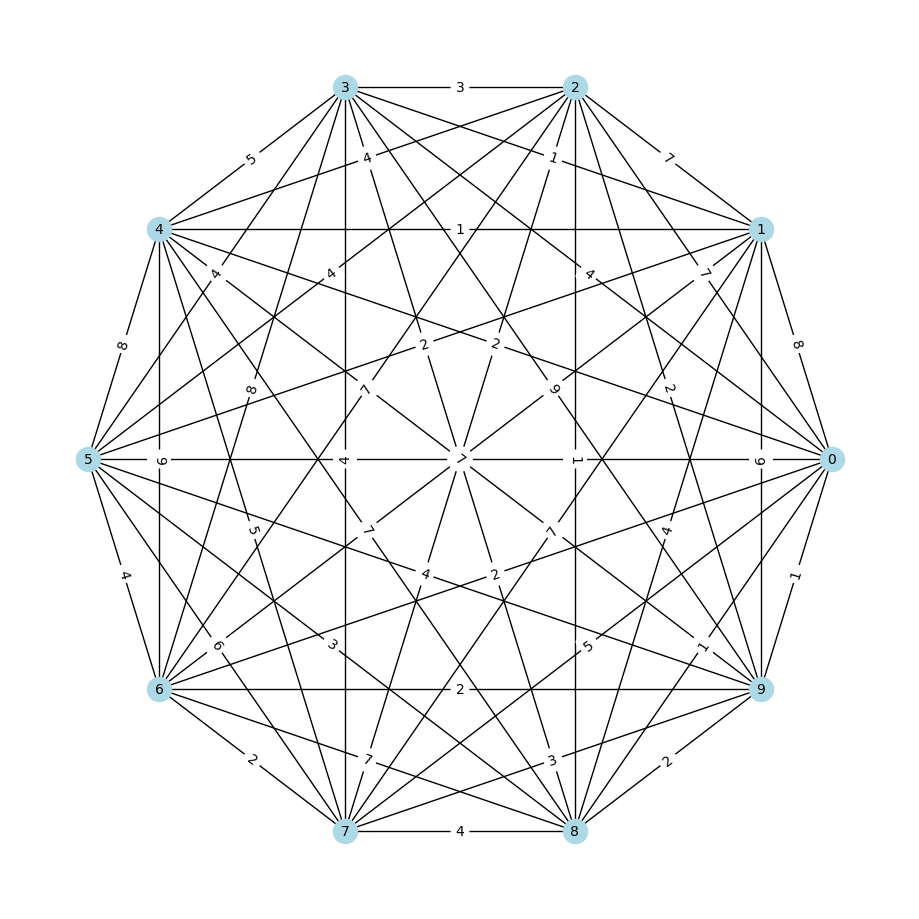
Рисунок 2- Созданный граф

Построено кластерное дерево по алгоритму агломеративной иерархической кластеризации WPGMA (метод группы взвешенных пар со средним арифметическим) (Рисунок 3-4).

Сначала каждая точка данных назначается отдельному кластеру.Находятся два ближайших кластера на основе попарных расстояний и объединяются в один кластер. Расстояние между двумя кластерами рассчитывается как среднее попарное расстояние между их членами, взвешенное по их соответствующим весам. Обновляются попарные расстояния между новым кластером и всеми оставшимися кластерами. Расстояние между новым кластером и любым другим кластером рассчитывается как среднее попарное расстояние между членами нового кластера и элементами другого кластера, взвешенное по их соответствующим весам.

Все шаги повторяются пока все точки данных не будут принадлежать одному кластеру.

Листинг 2- Построение кластерного дерева по алгоритму

import scipy.cluster.hierarchy as sch

# Применение алгоритма WPGMA

linked = sch.linkage(adj_matrix, method='average')

# Построение дендрограммы

plt.figure(figsize=(10, 9))

sch.dendrogram(linked, labels=np.arange(N))

plt.title("Дендрограмма по алгоритму WPGMA")

plt.xlabel("Вершины")

plt.ylabel("Расстояние")

plt.show()

#Визуализация кластерного дерева в виде графа

G = nx.Graph()

# Создание узлов для графа

for i in range(N):

G.add_node(i, label=f"Node {i}", level=0)

# Создание рёбер для графа на основе результатов кластеризации для каждого шага кластеризации :

# добавляются ребра от этого кластера к двум объединяемым кластерам

cluster_heights = {i: 0 for i in range(N)}

for i, (c1, c2, dist, _) in enumerate(linked):

new_cluster_id = N + i

G.add_node(new_cluster_id, label=f"Cluster {i + 1}", level=i + 1)

height_c1 = cluster_heights[int(c1)]

height_c2 = cluster_heights[int(c2)]

# Обновляение расстояний

G.add_edge(new_cluster_id, int(c1), weight=round(dist - height_c1, 2))

G.add_edge(new_cluster_id, int(c2), weight=round(dist - height_c2, 2))

# Обновление расстояния нового кластера

cluster_heights[new_cluster_id] = dist

# Определение позиции узлов для отрисовки снизу вверх и по горизонтали на каждом уровне

R = sch.dendrogram(linked, no_plot=True)# Получаем информацию о дендрограмме, построенной на основе результатов WPGMA

pos = {}#словарь который будет хранить координаты положения узлов графа

for i, pid in enumerate(R['leaves']):

pos[pid] = (i, 0) #Расположение листовых узлов горизонтально

for i, (c1, c2, _, _) in enumerate(linked):

pos[N + i] = ((pos[int(c1)][0] + pos[int(c2)][0]) / 2, i + 1) # Определяет расположение кластерных узлов относительно листовых узлов

labels = nx.get_node_attributes(G, 'label')

weights = nx.get_edge_attributes(G, 'weight')

plt.figure(figsize=(17, 20))

nx.draw(G, pos, with_labels=True, labels=labels, node_size=3000, node_color='lightblue', font_size=10, font_color='black', arrows=False)

nx.draw_networkx_edge_labels(G, pos, edge_labels=weights, font_size=15)

plt.title("Кластерное дерево (WPGMA) в виде графа")

plt.show()

Рисунок 3- Дендограмма по алгоритму WPGMA

Рисунок 4- Кластерное дерево по алгоритму WPGMA

Вывод: Реализовано кластерное дерево с использованием алгоритма WPGMA.

ПРИЛОЖЕНИЕ

import numpy as np

import networkx as nx

import matplotlib.pyplot as plt

N = 10

# Генерация случайных весов для верхнего треугольника матрицы

upper_triangle = np.random.randint(1, 10, size=(N, N))

np.fill_diagonal(upper_triangle, 0)

upper_triangle = np.triu(upper_triangle)

adj_matrix = upper_triangle + upper_triangle.T - np.diag(upper_triangle.diagonal())

print("Матрица смежности графа:")

print(adj_matrix)

G = nx.from_numpy_array(adj_matrix)

plt.figure(figsize=(9, 9))

pos = nx.circular_layout(G)

nx.draw(G, pos, with_labels=True, node_size=300, node_color='lightblue', font_size=10)

edge_labels = {(i, j): adj_matrix[i][j] for i in range(N) for j in range(N) if adj_matrix[i][j] != 0}

nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

plt.show()

import scipy.cluster.hierarchy as sch

# Применение алгоритма WPGMA

linked = sch.linkage(adj_matrix, method='average')

# Построение дендрограммы

plt.figure(figsize=(10, 9))

sch.dendrogram(linked, labels=np.arange(N))

plt.title("Дендрограмма по алгоритму WPGMA")

plt.xlabel("Вершины")

plt.ylabel("Расстояние")

plt.show()

#Визуализация кластерного дерева в виде графа

G = nx.Graph()

# Создание узлов для графа

for i in range(N):

G.add_node(i, label=f"Node {i}", level=0)

# Создание рёбер для графа на основе результатов кластеризации для каждого шага кластеризации :

# добавляются ребра от этого кластера к двум объединяемым кластерам

cluster_heights = {i: 0 for i in range(N)}

for i, (c1, c2, dist, _) in enumerate(linked):

new_cluster_id = N + i

G.add_node(new_cluster_id, label=f"Cluster {i + 1}", level=i + 1)

height_c1 = cluster_heights[int(c1)]

height_c2 = cluster_heights[int(c2)]

# Обновляение расстояний

G.add_edge(new_cluster_id, int(c1), weight=round(dist - height_c1, 2))

G.add_edge(new_cluster_id, int(c2), weight=round(dist - height_c2, 2))

# Обновление расстояния нового кластера

cluster_heights[new_cluster_id] = dist

# Определение позиции узлов для отрисовки снизу вверх и по горизонтали на каждом уровне

R = sch.dendrogram(linked, no_plot=True)# Получаем информацию о дендрограмме, построенной на основе результатов WPGMA

pos = {}#словарь который будет хранить координаты положения узлов графа

for i, pid in enumerate(R['leaves']):

pos[pid] = (i, 0) #Расположение листовых узлов горизонтально

for i, (c1, c2, _, _) in enumerate(linked):

pos[N + i] = ((pos[int(c1)][0] + pos[int(c2)][0]) / 2, i + 1) # Определяет расположение кластерных узлов относительно листовых узлов

labels = nx.get_node_attributes(G, 'label')

weights = nx.get_edge_attributes(G, 'weight')

plt.figure(figsize=(17, 20))

nx.draw(G, pos, with_labels=True, labels=labels, node_size=3000, node_color='lightblue', font_size=10, font_color='black', arrows=False)

nx.draw_networkx_edge_labels(G, pos, edge_labels=weights, font_size=15)

plt.title("Кластерное дерево (WPGMA) в виде графа")

plt.show()