Цель работы: рассмотреть различные подходы к генерации случайных графов в ЭВМ. Провести анализ свойств созданных графов.

Индивидуальный вариант:

Вариант № 21

На рисунке 1-2 представлен тип случайного графа и свойство случайного графа согласно индивидуальному варианту.

Рисунок 1- Тип случайного графа

Рисунок 2- Свойство случайного графа

Ход работы

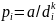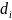Создан граф с помощью алгоритма, при котором добавляется новая вершина, для которой выбирается только один сосед из уже существующих вершин. Вероятность выбора i-ой вершины как соседа , где - степень i-ой вершины (количество ее соседей в графе) (Рисунок 1).

Листинг 1. Алгоритм создания графа

import numpy as np

import networkx as nx

import matplotlib.pyplot as plt

def create_adjacency_matrix(N, k):

adj_matrix = np.zeros((N, N))

degrees = [0] * N

for i in range(1, N): # Начало со второй вершины

# Вычисление вероятностей для новой вершины

probs = [1 / (degrees[j] ** k + 1) for j in range(i)]

# Нормализация вероятностей, чтобы их сумма равнялась 1

probs = probs / np.sum(probs)

# Выбор соседа для новой вершины на основе вычисленных вероятностей

neighbor = np.random.choice(range(i), p=probs)

# Обновление матрицы смежности

adj_matrix[i, neighbor] = 1

adj_matrix[neighbor, i] = 1

# Увеличение степеней

degrees[i] += 1

degrees[neighbor] += 1

return adj_matrix

N = 10

k = 2

adjacency_matrix = create_adjacency_matrix(N, k)

G = nx.from_numpy_array(adjacency_matrix)

pos = nx.spring_layout(G)

nx.draw(G, pos, with_labels=True, node_size=300, node_color='lightblue', font_size=10)

plt.axis('off')

plt.show()

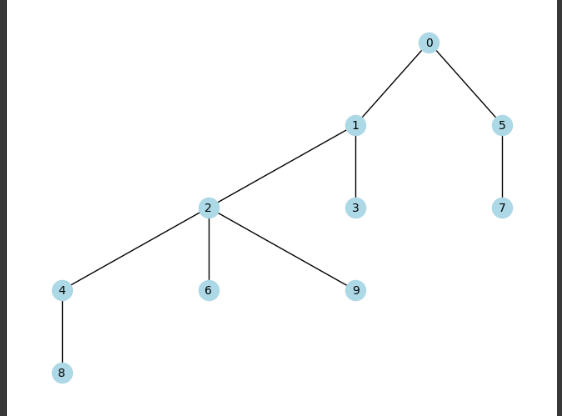
Рисунок 1- Созданный граф

Реализована функция поиска спектра степеней графа, визуализирован полученный спектр (гистограмма распределения частот степеней всех вершин графа). (Рисунок 2).

Листинг 2- Поиск спектра степеней и его визуализация

def get_degree_spectrum(G):

# Словарь для хранения количества вершин для каждой степени

degree_counts = {}

# Проход по всем вершинам графа и получение их степени

for degree in dict(G.degree()).values():

# Если степень уже встречалась, увеличичение счетчика

if degree in degree_counts:

degree_counts[degree] += 1

# Иначе добавление степени в словарь\

else:

degree_counts[degree] = 1

return degree_counts

degree_spectrum = get_degree_spectrum(G)

plt.figure(figsize=(8, 6))

plt.bar(degree_spectrum.keys(), degree_spectrum.values(), color='indigo')

plt.xlabel('Степень вершины')

plt.ylabel('Количество вершин')

plt.title('Спектр степеней графа')

plt.show()

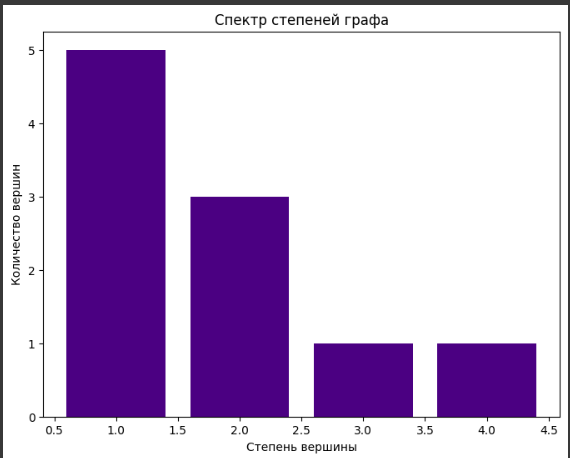
Рисунок 2- Гистограмма распределения частот степеней всех вершин графа

Построен график зависимости среднего диаметра графа от количества вершин при k=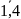 . (Рисунок 4-5).

Листинг 3- График зависимости среднего диаметра графа от количества вершин

def average_diameter(k_values, num_of_repeat, max_vertices):

results = {}

for k in k_values:

diameters = []

for N in range(2, max_vertices + 1):

avg_diameter = 0

# Выполнение повторений для усреднения

for _ in range(num_of_repeat):

adjacency_matrix = create_adjacency_matrix(N, k) # Создание матрицы смежности

G = nx.from_numpy_array(adjacency_matrix) # Создание графа из матрицы смежности

diameter = nx.diameter(G) # Вычисление диаметра графа

avg_diameter += diameter # Суммирование диаметров

avg_diameter /= num_of_repeat # Вычисление среднего диаметра

diameters.append(avg_diameter)

results[k] = diameters

return results

k_values = [1, 2, 3, 4]

num_of_repeat = 100 # Количество повторений

max_vertices = 30

results = average_diameter(k_values, num_of_repeat, max_vertices)

fig = plt.figure(figsize=(10, 8))

# Построение всех кривых на одном графике

for k in k_values:

plt.plot(range(2, max_vertices + 1), results[k], label=f'k={k}')

plt.xlabel('Количество вершин')

plt.ylabel('Средний диаметр')

plt.title('Средний диаметр в зависимости от количества вершин и параметра k')

plt.grid(True)

plt.legend()

plt.tight_layout()

plt.show()

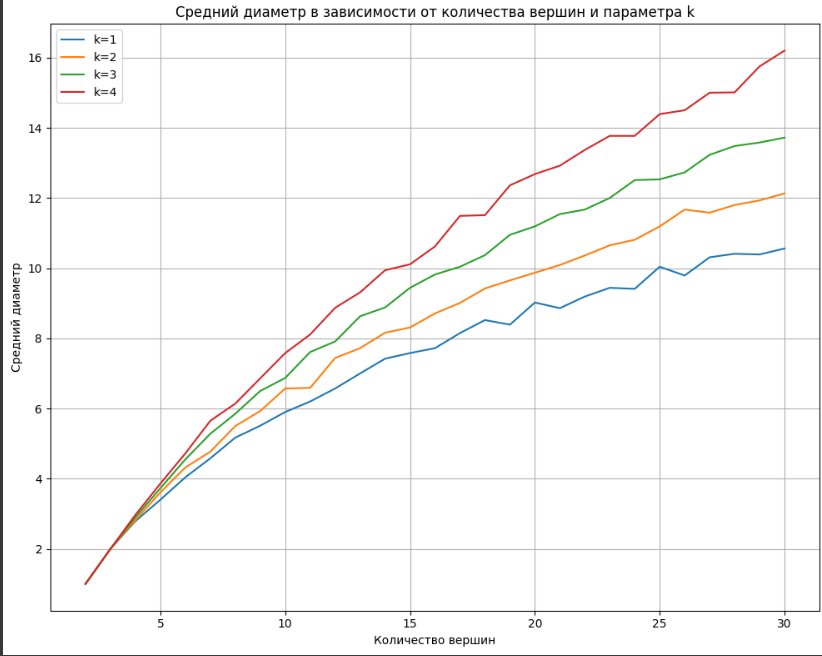
Рисунок 3- График зависимости среднего диаметра графа от количества вершин при разном значении k

На графике наблюдается тенденция увеличения среднего диаметра графа по мере увеличения количества вершин.

С ростом параметра k средний диаметр графа увеличивается для одинакового числа вершин. Увеличение параметра k приводит к тому, что новые рёбра чаще добавляются к вершинам с меньшей степенью, делая граф более равномерно распределённым.

Графики помогают понять, как изменения в параметрах генерации влияют на свойства графов.

Построены спектры степеней графа для разных значений k (Рисунок 4).

Листинг 4- Спектры степеней графа для разных значений k

def calculate_degree_spectr(k, max_vertices, num_of_repeat):

degree_spectra = []

for N in range(2, max_vertices + 1):

degree_counts = {}

for _ in range(num_of_repeat):

adjacency_matrix = create_adjacency_matrix(N, k)

G = nx.from_numpy_array(adjacency_matrix)

degree_spectrum = get_degree_spectrum(G)

for degree, count in degree_spectrum.items():

degree_counts[degree] = degree_counts.get(degree, 0) + count

degree_spectra.append({degree: np.round(count / num_of_repeat) for degree, count in degree_counts.items()})

return degree_spectra

k_values = [1, 2, 3, 4]

num_of_repeat = 100

max_vertices = 30

degree_spectr = {k: calculate_degree_spectr(k, max_vertices, num_of_repeat) for k in k_values}

fig = plt.figure(figsize=(12, 12))

for i, k in enumerate(k_values):

plt.subplot(2, 2, i+1)

for degree_spectrum in degree_spectr[k]:

degrees = sorted(degree_spectrum.keys())

counts = [degree_spectrum[d] for d in degrees]

plt.bar(degrees, counts, color='indigo')

plt.xlabel('Степень вершины')

plt.ylabel('Количество вершин')

plt.title(f'k={k}')

plt.tight_layout()

plt.show()

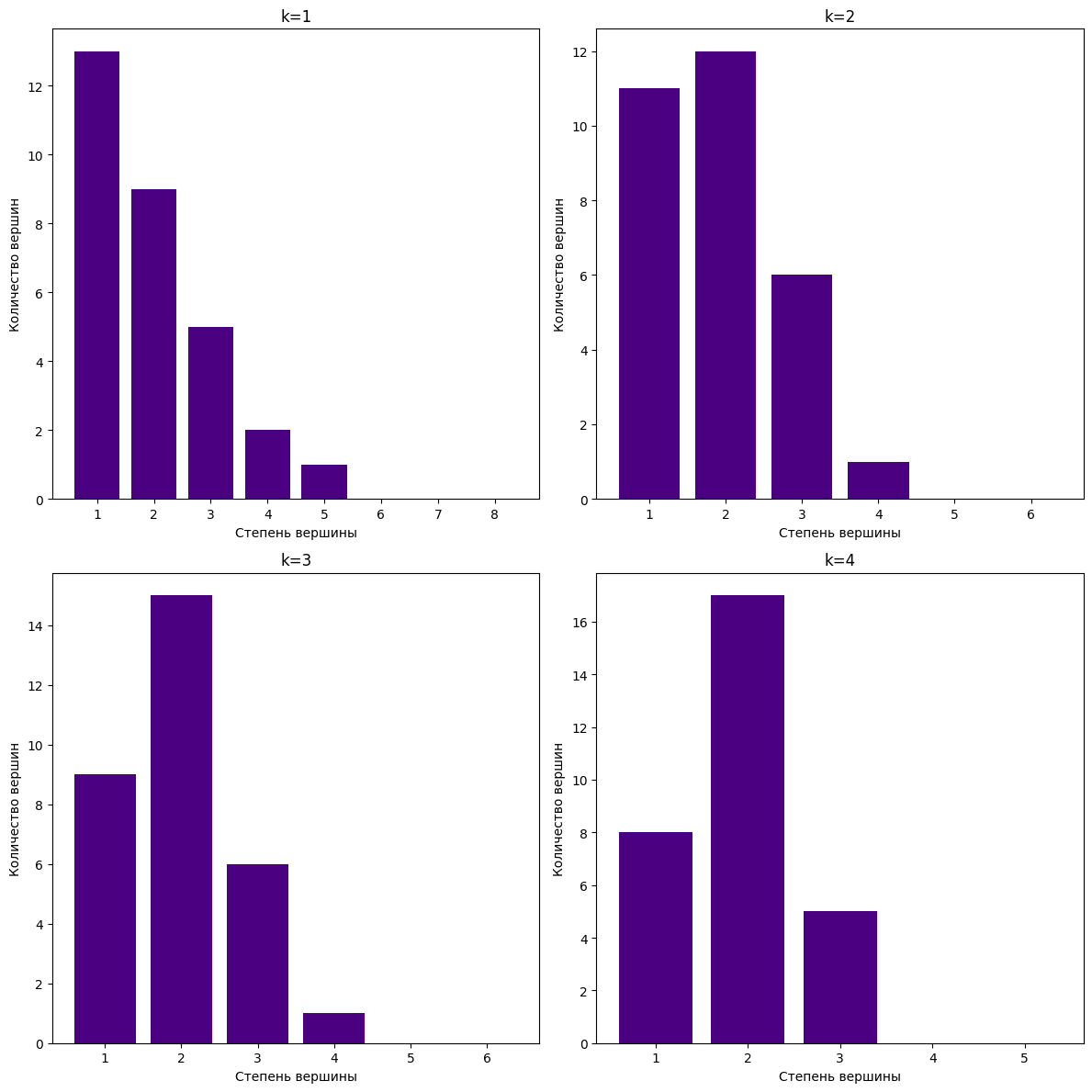
Рисунок 4- Спектры степеней графа для разных значений k

С увеличением параметра k, вершины имеют меньше инцидентных ребер, граф становится менее связанным.

Вывод:

С помощью алгоритма построен граф в виде дерева, построен спектр степеней графа, который показывает распределение частот степеней всез вершин графа. Построены 4 графика зависимости среднего диаметра графа от количества вершин при разных значениях k. Чем больше значение k, тем меньше инцидентных ребер имеют вершины.

Приложение

Import numpy as np

Import networkx as nx

Import matplotlib.Pyplot as plt

from networkx.drawing.nx_pydot import graphviz_layout

def create_adjacency_matrix(N, k):

adj_matrix = np.zeros((N, N))

degrees = [0] * N

for i in range(1, N): # Начало со второй вершины

# Вычисление вероятностей для новой вершины

probs = [1 / (degrees[j] ** k + 1) for j in range(i)]

# Нормализация вероятностей, чтобы их сумма равнялась 1

probs = probs / np.sum(probs)

# Выбор соседа для новой вершины на основе вычисленных вероятностей

neighbor = np.random.choice(range(i), p=probs)

# Обновление матрицы смежности

adj_matrix[i, neighbor] = 1

adj_matrix[neighbor, i] = 1

# Увеличение степеней

degrees[i] += 1

degrees[neighbor] += 1

return adj_matrix

N = 10

k = 2

adjacency_matrix = create_adjacency_matrix(N, k)

G = nx.from_numpy_array(adjacency_matrix)

pos = graphviz_layout(G, prog="dot")

nx.draw(G, pos, with_labels=True, node_size=300, node_color='lightblue', font_size=10)

plt.axis('off')

plt.show()

def get_degree_spectrum(G):

# Словарь для хранения количества вершин для каждой степени

degree_counts = {}

# Проход по всем вершинам графа и получение их степени

for degree in dict(G.degree()).values():

# Если степень уже встречалась, увеличичение счетчика

if degree in degree_counts:

degree_counts[degree] += 1

# Иначе добавление степени в словарь

else:

degree_counts[degree] = 1

return degree_counts

degree_spectrum = get_degree_spectrum(G)

plt.figure(figsize=(8, 6))

plt.bar(degree_spectrum.keys(), degree_spectrum.values(), color='indigo')

plt.xlabel('Степень вершины')

plt.ylabel('Количество вершин')

plt.title('Спектр степеней графа')

plt.show()

def average_diameter(k_values, num_of_repeat, max_vertices):

results = {}

for k in k_values:

diameters = []

for N in range(2, max_vertices + 1):

avg_diameter = 0

# Выполнение повторений для усреднения

for _ in range(num_of_repeat):

adjacency_matrix = create_adjacency_matrix(N, k) # Создание матрицы смежности

G = nx.from_numpy_array(adjacency_matrix) # Создание графа из матрицы смежности

diameter = nx.diameter(G) # Вычисление диаметра графа

avg_diameter += diameter # Суммирование диаметров

avg_diameter /= num_of_repeat # Вычисление среднего диаметра

diameters.append(avg_diameter)

results[k] = diameters

return results

k_values = [1, 2, 3, 4]

num_of_repeat = 100 # Количество повторений

max_vertices = 30

results = average_diameter(k_values, num_of_repeat, max_vertices)

fig = plt.figure(figsize=(10, 8))

# Построение всех кривых на одном графике

for k in k_values:

plt.plot(range(2, max_vertices + 1), results[k], label=f'k={k}')

plt.xlabel('Количество вершин')

plt.ylabel('Средний диаметр')

plt.title('Средний диаметр в зависимости от количества вершин и параметра k')

plt.grid(True)

plt.legend()

plt.tight_layout()

plt.show()

def calculate_degree_spectr(k, max_vertices, num_of_repeat):

degree_spectra = []

for N in range(2, max_vertices + 1):

degree_counts = {}

for _ in range(num_of_repeat):

adjacency_matrix = create_adjacency_matrix(N, k)

G = nx.from_numpy_array(adjacency_matrix)

degree_spectrum = get_degree_spectrum(G)

for degree, count in degree_spectrum.items():

degree_counts[degree] = degree_counts.get(degree, 0) + count

degree_spectra.append({degree: np.round(count / num_of_repeat) for degree, count in degree_counts.items()})

return degree_spectra

k_values = [1, 2, 3, 4]

num_of_repeat = 100

max_vertices = 30

# словарь degree_spectr, в котором ключами являются значения k, а значениями - списки спектров степеней

degree_spectr = {k: calculate_degree_spectr(k, max_vertices, num_of_repeat) for k in k_values}

fig = plt.figure(figsize=(12, 12))

for i, k in enumerate(k_values):

plt.subplot(2, 2, i+1)

for degree_spectrum in degree_spectr[k]:

degrees = sorted(degree_spectrum.keys())

counts = [degree_spectrum[d] for d in degrees]

plt.bar(degrees, counts, color='indigo')

plt.xlabel('Степень вершины')

plt.ylabel('Количество вершин')

plt.title(f'k={k}')

plt.tight_layout()

plt.show()