Графы1_

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				М.Н. Шелест
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

ПРЕДСТАВЛЕНИЕ ГРАФОВ В ЭВМ

по курсу: ПОСТРОЕНИЕ И АНАЛИЗ ГРАФОВЫХ МОДЕЛЕЙ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
				подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: Изучение представления графов в ЭВМ при помощи матрицы смежности, множества пар вершин и массива структур. Визуализация графов.

Индивидуальный вариант:

Вариант №1 (21)

На рисунке 1 представлен граф

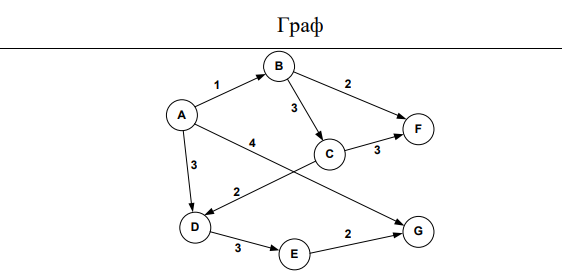
Рисунок 1- Граф по варианту

В таблице 1 представлена матрица смежности графа Таблица 1

	A	B	C	D	E	F	G
A	0	1	0	3	0	0	4
B	0	0	3	0	0	2	0
C	0	0	0	2	0	3	0
D	0	0	0	0	3	0	0
E	0	0	0	0	0	0	2
F	0	0	0	0	0	0	0
G	0	0	0	0	0	0	0

Матрица смежности введена в ЭВМ в явном виде (Листинг 1)

Листинг. Введение матрицы смежности в явном виде

peaks = ['A', 'B', 'C', 'D', 'E', 'F', 'G']

matrix = [

[0, 1, 0, 3, 0, 0, 4],

[0, 0, 3, 0, 0, 2, 0],

[0, 0, 0, 2, 0, 3, 0],

[0, 0, 0, 0, 3, 0, 0],

[0, 0, 0, 0, 0, 0, 2],

[0, 0, 0, 0, 0, 0, 0],

[0, 0, 0, 0, 0, 0, 0]

]

Из заданной матрицы смежности написана программа для вывода списка ребер (Рисунок 2).

Листинг. Вывод списка ребер графа

def matrix_to_edge_list(peaks, matrix):

edge_list = []

for i in range(len(peaks)):

for j in range(len(peaks)):

if matrix[i][j] != 0:

edge_list.append((peaks[i], peaks[j], matrix[i][j]))

return edge_list

edge_list = matrix_to_edge_list(peaks, matrix)

for edge in edge_list:

print(edge[0], '->', edge[1], ':', edge[2])

Рисунок 2- Вывод списка ребер из заданной матрицы смежности

Написана программа для визуализации графа, результат программы показан на рисунке 3.

Листинг 3- Построение графа

G = nx.DiGraph()

G.add_nodes_from(peaks)

G.add_weighted_edges_from(edge_list)

plt.figure()

# Определение позиций узлов на графе с помощью алгоритма раскладки

pos = nx.circular_layout(G)

# Отрисовка графа с узлами размером 2000, с позициями pos и подписями для узлов

nx.draw(G, node_size=2000, pos=pos, with_labels=True)

# Получение атрибутов весов рёбер и отрисовка их меток

edge_labels = nx.get_edge_attributes(G, "weight")

nx.draw_networkx_edge_labels(G, pos, edge_labels)

plt.show()

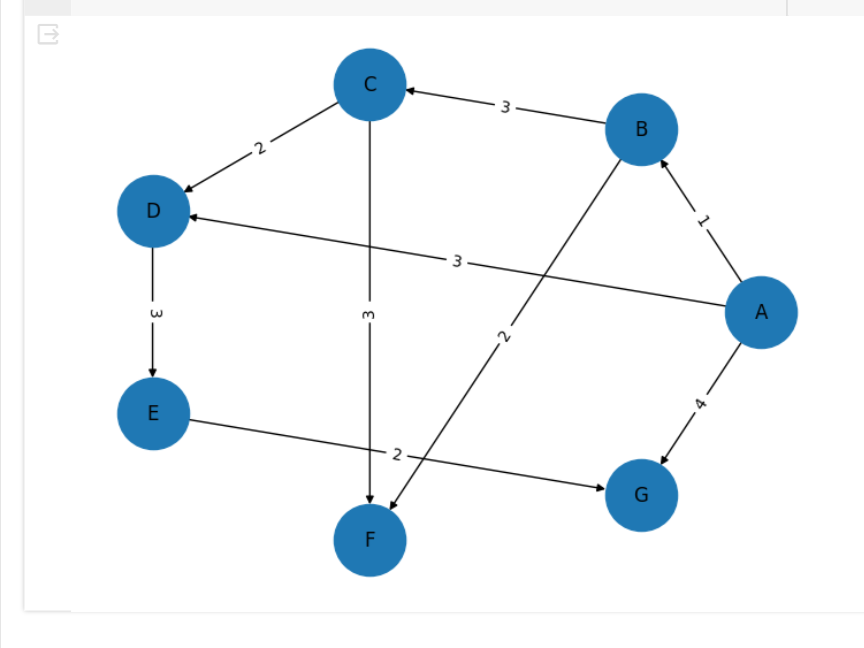
Рисунок 3- Результат работы программы построения графа

Далее написана подпрограмма для представления графа в виде массива записей, основанном на матрице смежности (Рисунок 4).

Листинг 4- Представление графа в виде массива записей

def matrix_to_records(peaks, matrix):

records = []

num_vertices = len(peaks) # Количество вершин в графе

for i, label in enumerate(peaks):

# Находим детей текущей вершины (вершины, к которым есть ребра из текущей вершины)

children = [j for j in range(num_vertices) if matrix[i][j] != 0]

# Находим родителей текущей вершины (вершины, из которых есть ребра в текущую вершину)

parents = [j for j in range(num_vertices) if matrix[j][i] != 0]

# Находим всех соседей текущей вершины (вершины, с которыми текущая вершина связана)

neighbors = list(set(children + parents))

# Получаем веса исходящих рёбер из текущей вершины

outgoing_edge_weights = [matrix[i][j] for j in children]

# Получаем веса входящих рёбер в текущую вершину

incoming_edge_weights = [matrix[j][i] for j in parents]

# Веса инцидентных рёбер текущей вершины

incident_edge_weights = [matrix[i][j] for j in neighbors]

# Имена детей текущей вершины

children_names = [peaks[j] for j in children]

# Имена родителей текущей вершины

parents_names = [peaks[j] for j in parents]

# Создаем запись для текущей вершины

record = {

'№ вершины': i, # Номер вершины

'Имя вершины': label, # Имя вершины

'Количество детей': len(children), # Количество детей текущей вершины

'Дети': children_names, # Имена детей текущей вершины

'Веса исходящих ребер': outgoing_edge_weights, # Веса исходящих рёбер из текущей вершины

'Количество родителей': len(parents), # Количество родителей текущей вершины

'Родители': parents_names, # Имена родителей текущей вершины

'Веса входящих ребер': incoming_edge_weights, # Веса входящих рёбер в текущую вершину

'Количество соседей': len(neighbors), # Количество соседей текущей вершины

'Соседи': [peaks[j] for j in neighbors], # Имена соседей текущей вершины

'Веса инцидентных ребер': incident_edge_weights # Веса инцидентных рёбер текущей вершины

}

records.append(record)

return pd.DataFrame(records)

df = matrix_to_records(peaks, matrix)

display(df)

Рисунок 4- Результат работы программы представления графа в виде массива записей

Для каждого представления написана подпрограмма для вывода всех соседей вершины графа (Рисунок 5-7)

Листинг 4- Поиск соседей вершины графа для матрицы смежности

def neighbors_matrix(vertex, matrix):

neighbors = []

num_vertices = len(matrix)

for i in range(num_vertices):

if matrix[vertex][i] != 0:

neighbors.append(i)

for i in range(num_vertices):

if matrix[i][vertex] != 0:

neighbors.append(i)

return neighbors

# vertex = int(input("Введите номер вершины для поиска соседей: "))

# result = neighbors_matrix(vertex, matrix)

# print(f"Соседи выбранной вершины: {result}")

Рисунок 5- результат работы программы поиска соседей вершины графа для матрицы смежности

Листинг 5- Поиск соседей вершины графа для списка ребер

def neighbors_edge_list(vertex, edge_list):

neighbors = []

for edge in edge_list:

if edge[0] == vertex:

neighbors.append(edge[1])

elif edge[1] == vertex:

neighbors.append(edge[0])

return neighbors

# vertex = input("Введите имя вершину для поиска соседей: ")

# result = neighbors_edge_list(vertex, edge_list)

# print(f"Соседи выбранной вершины: {result}")

Рисунок 6- Результат работы программы поиска соседей вершины графа для списка ребер

Листинг 6- Поиск соседей вершины графа для массива записей

def neighbors_records(vertex, records):

for record in records:

if record['Имя вершины'] == vertex:

return record['Соседи']

# vertex = input("Введите имя вершины для поиска соседей: ")

# result = neighbors_records(vertex, df.to_dict('records'))

# print(f"Соседи выбранной вершины: {result}")

Рисунок 7- Результат работы программы поиска соседей вершины графа для массива записей

Также написаны подпрограммы для вывода ответа, образует ли заданная последовательность вершин цепь.

Листинг 7- Образует ли заданная последовательность вершин цепь для матрицы смежности

def is_chain_adjacency_matrix(vertices, matrix):

visited_edges = set() # множество для отслеживания посещенных рёбер

prev_vertex = None # переменная для хранения предыдущей вершины

for vertex in vertices:

prev_vertex = vertex

for i in range(len(vertices) - 1):

source = vertices[i]

target = vertices[i + 1]

if matrix[source][target] == 0 or (source, target) in visited_edges:

return False

visited_edges.add((source, target)) # Добавление ребра в множество посещенных рёбер

return True

chain = list(map(int, input("Введите последовательность вершин через пробел: ").split()))

print("Образует ли заданная последовательность вершин цепь:", is_chain_adjacency_matrix(chain, matrix))

Листинг 8- Образует ли заданная последовательность вершин цепь для списка ребер

def edgesList_is_chain(edges, vertices):

visited_edges = set() # Множество для отслеживания посещенных рёбер

for i in range(len(vertices) - 1):

edge = (vertices[i], vertices[i + 1])

if edge not in [(x[:2]) for x in edges]:

return False

if edge in visited_edges: # Проверка наличия повторяющегося ребра

return False

visited_edges.add(edge) # Добавление ребра в множество посещенных рёбер

return True

vertices= input("Введите последовательность имен вершин через пробел: ").split()

print("Образует ли заданная последовательность вершин цепь:", edgesList_is_chain(edge_list, vertices))

Листинг 9- Образует ли заданная последовательность вершин цепь для массива записей

def is_chain_records(vertices, records):

visited_edges = set() # множество для отслеживания посещенных рёбер

for i in range(len(vertices) - 1):

current_vertex = vertices[i]

next_vertex = vertices[i + 1]

found = False

for record in records:

if record['Имя вершины'] == current_vertex:

if next_vertex in record['Дети']:

edge = (current_vertex, next_vertex)

if edge in visited_edges: # Проверка

return False

else:

visited_edges.add(edge)

found = True

break

if not found:

return False

return True

# chain = input("Введите последовательность имен вершин через пробел: ").split()

# print("Образует ли заданная последовательность вершин цепь:", is_chain_records(chain, df.to_dict('records')))

Были написаны подпрограммы для вывода номеров вершин, сумма весов инцидентных ребер которых больше.

Листинг 10- Вывод номеров вершин, сумма весов инцидентных ребер которых больше для матрицы смежности

def matrix_nodes_with_large_incident_edges(matrix, threshold):

nodes = []

for i in range(len(matrix)):

incident_edges_sum = sum(matrix[i]) + sum(row[i] for row in matrix)

if incident_edges_sum > threshold:

nodes.append(i)

return nodes

# threshold = int(input("Введите пороговое значение суммы весов: "))

# print(matrix_nodes_with_large_incident_edges(matrix, threshold))

Листинг 11- Вывод номеров вершин, сумма весов инцидентных ребер которых больше для списка ребер

def nodes_with_large_incident_edges(edges, threshold):

incident_edges_sum = {}

for edge in edges:

source, target, weight = edge

incident_edges_sum[source] = incident_edges_sum.get(source, 0) + weight

incident_edges_sum[target] = incident_edges_sum.get(target, 0) + weight

nodes = [node for node, weight_sum in incident_edges_sum.items() if weight_sum > threshold]

return nodes

# threshold = int(input("Введите пороговое значение суммы весов: "))

# result = nodes_with_large_incident_edges(edge_list, threshold)

# print("Вершины с суммой весов инцидентных рёбер больше {}: {}".format(threshold, result))

Листинг 12- Вывод номеров вершин, сумма весов инцидентных ребер которых больше для массива записей

def df_nodes_with_large_incident_edges(df, threshold):

above_threshold = []

for index, row in df.iterrows():

weights_sum = sum(row['Веса инцидентных ребер'])

if weights_sum > threshold:

above_threshold.append(row['Имя вершины'])

return above_threshold

# threshold = int(input("Введите пороговое значение суммы весов: "))

# result = df_nodes_with_large_incident_edges(df, threshold)

# print("Вершины с суммой весов инцидентных рёбер больше {}: {}".format(threshold, result))

Написаны подпрограммы для вывода количества ребер в графе для всех представлений

Листинг 13- Вывод количества ребер в графе для матрицы смежности

def count_edges_adjacency_matrix(matrix):

count = 0

for row in matrix:

count += sum(1 for weight in row if weight != 0)

return count

# result = count_edges_adjacency_matrix(matrix)

# print("Количество ребер в графе:", result)

Листинг 14- Вывод количества ребер в графе для списка ребер

def count_edges_edge_list(edge_list):

return len(edge_list)

# count = count_edges_edge_list(edge_list)

# print("Количество рёбер в графе :", count)

Листинг 15- Вывод количества ребер в графе для массива записей

def df_count_edges(df):

return df['Количество детей'].sum()

# print(df_count_edges(df))

Для каждого представления посчитан размер содержащего их объекта в байтах и выведен в датафрейм (Рисунок 8).

Листинг 16- Подсчет размера содержащего объекта представлений в байтах.

import sys

import pandas as pd

size_of_matrix = sys.getsizeof(matrix)

size_of_edge_list = sys.getsizeof(edge_list)

size_of_records = sys.getsizeof(df)

sizes_df = pd.DataFrame({

'Представление': ['Матрица смежности', 'Список рёбер', 'Массив записей'],

'Размер в байтах': [size_of_matrix, size_of_edge_list, size_of_records]

})

print(sizes_df)

Рисунок 8- Датафрейм с размерами

Результат показывает, что Матрица смежности имеет наименьший размер, затем идет список ребер, а массив записей требует наибольшего объема памяти.

Далее подсчитано время выполнения каждой подпрограммы всех представлений и выведено на экран (Рисунок 9-11).

Рисунок 9- Результат работы программы для подсчета времени выполнения подпрограмм для матрицы смежности

Листинг 17- Подсчет времени выполнения подпрограмм для матрицы смежности

num_iterations = 10**6

vertex = 1

vertices = [0, 1, 5]

threshold = 5

print("Матрица смежности, время выполнения функций")

df_results = pd.DataFrame()

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

neighbors_matrix(vertex,matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "neighbors_matrix", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

is_chain_adjacency_matrix(vertices, matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': " is_chain_adjacency_matrix", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

matrix_nodes_with_large_incident_edges(matrix, threshold)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "matrix_nodes_with_large_incident_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

count_edges_adjacency_matrix(matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

#################################

pd.set_option('display.float_format', '{:.7f}'.format)

df_results = df_results.append({'Функция': "count_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

df_results

Рисунок 10 - Результат работы программы для подсчета времени выполнения подпрограмм для списка ребер

Листинг 18- Подсчет времени выполнения подпрограмм для списка ребер

num_iterations = 10**6

vertex = 1

vertices = [0, 1, 5]

threshold = 5

print("Матрица смежности, время выполнения функций")

df_results = pd.DataFrame()

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

neighbors_matrix(vertex,matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "neighbors_matrix", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

is_chain_adjacency_matrix(vertices, matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': " is_chain_adjacency_matrix", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

matrix_nodes_with_large_incident_edges(matrix, threshold)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "matrix_nodes_with_large_incident_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

count_edges_adjacency_matrix(matrix)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

#################################

pd.set_option('display.float_format', '{:.7f}'.format)

df_results = df_results.append({'Функция': "count_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

df_results

Рисунок 11 - Результат работы программы для подсчета времени выполнения подпрограмм для массива записей

Листинг 19- Подсчет времени выполнения подпрограмм для списка ребер

num_iterations = 10**6

total_time = 0

vertex= 'A'

vertices = ['A', 'B', 'C']

threshold = 30

print("Датафрейм, скорость выполнения функций")

df_results = pd.DataFrame()

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

neighbors_records(vertex, df.to_dict('records'))

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "neighbors_records", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

is_chain_records(vertices, df.to_dict('records'))

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': " is_chain_records", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

df_nodes_with_large_incident_edges(df, threshold)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

df_results = df_results.append({'Функция': "df_nodes_with_large_incident_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

#################################

total_time = 0

for i in range(num_iterations):

start_time = time.time()

df_count_edges(df)

end_time = time.time()

total_time += end_time - start_time

average_time = total_time / num_iterations

#################################

df_results = df_results.append({'Функция': "df_count_edges", 'Время выполнения, сек': average_time}, ignore_index=True)

df_results

По результатам работ программ видно, что быстрей всего функции выполняет представление в виде списка ребер, все функции кроме edgesList_is_chain выполняются быстрее, чем в формате матрицы смежности. Дольше всего программы выполняет представление в виде массива записей.

Вывод:

В процессе выполнения лабораторной работы получены следующие выводы о целесообразности хранения структуры графа в рассмотренных представлениях:

Матрица смежности:

Занимает минимальный объем памяти при хранении.

Неэффективно использовать при разреженных графах, где большинство элементов матрицы равны нулю.

Список ребер:

Занимает меньше памяти, чем массив записей, и может быть более эффективным для больших графов с низкой плотностью ребер.

Массив записей:

Обеспечивает более удобный доступ к дополнительным атрибутам вершин или ребер, таким как веса.

Требует больше памяти, особенно для больших графов.