ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н.В. Апанасенко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ № 1

АНАЛИЗ ЭЛЕМЕНТАРНОЙ СИСТЕМЫ МНОЖЕСТВЕННОГО ДОСТУПА

по курсу: ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ, СЕТИ И ТЕЛЕКОММУНИКАЦИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ гр. №	4116
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

Цель работы: получение навыков моделирования алгоритмов случайного множественного доступа в системах передачи данных.

Теоретические сведения:

В данной лабораторной работе проводится моделирование работы сети, где случайным образом определяются два параметра: количество пользователей, поступивших в сеть за определенный временной интервал, и количество пользователей, передающих сообщения в эту сеть.

В соответствии с алгоритмом возможны три события:

1.) Событие «успех». Если в слоте передает только один абонент, считается, что сообщение доставлено успешно. Абонент, успешно передавший сообщение, покидает систему.

2) Событие «конфликт». Если в слоте передают два и более абонентов, то в этом случае считается, что сообщение не доставлено – произошел конфликт. Абоненты остаются в системе и осуществляют попытки передачи сообщения в следующих слотах.

3) Событие «пусто». В слоте не передает ни один из абонентов.

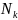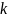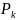Количество пользователей на слоте: , где -количество пользователей на слоте , – количество пользователей, подключившихся к сети, в данном слотеI – индикаторная функция.

P_k имеет пуассоновское распределени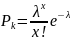е: , где 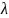– интенсивность (среднее количество абонентов, которое появляется в одном слоте), принимает значения  (0.05,0.5) с шагом 0.05.

R_k распределено по биномиальному закону распределения.

Ход работы:

С оставлена марковская модель переходных состояний (рисунок 1). Переходы в право осуществляются в любое состояние, обратные только на состояние назад

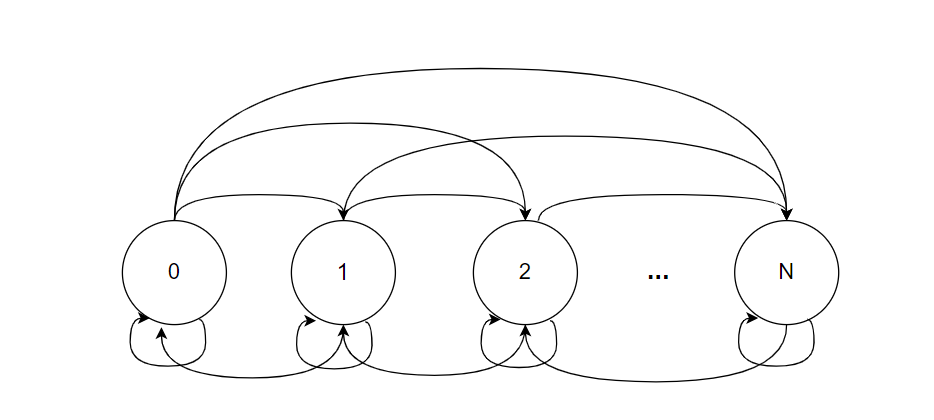
Рисунок 1 – Цепь Маркова по заданному алгоритму

Матрица переходных вероятностей:

В приложении А представлена программа для построения матрицы переходных состояний на языке Python (рисунок 2). Параметр  (0.05,0.5) с шагом 0.05.

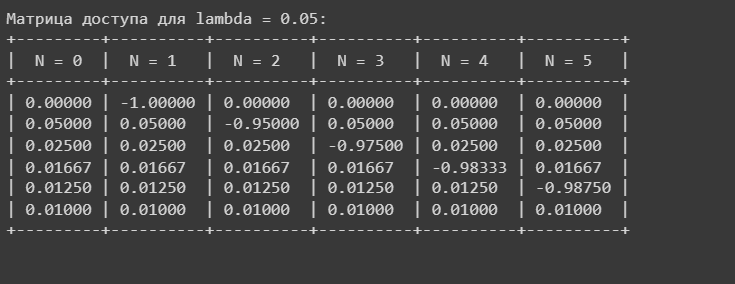
Рисунок 2- Матрица переходных вероятностей для значения =0.05

Происходит перебор всех значений лямбды с шагом 0,05. Для каждой лямбды случайным образом определяется количество пользователей, которое распределено по закону Пуассона. Затем для каждого временного слота определяется количество пользователей: количество пользователей в каждом слоте соответствует значению из распределения Пуассона. После этого с использованием биномиального распределения определяется количество пользователей, готовых передать сообщение.

Вероятность передачи сообщения одним пользователем – 1/N_k, если N_k равно нулю, то количество пользователей, передающих сообщение тоже равно нулю.

Исходя из количества пользователей, передающих сообщение, рассчитывается количество пользователей в слоте. Если сообщение передаёт 1 пользователь, то количество пользователей определяется как N_k+1 = N_k + P_k -1, в остальных случаях – N_k+1 = N_k + P_k.

Среднее количество абонентов в системе N вычисляется для каждой лямбды путем деления суммы пользователей на каждом слоте на количество слотов.

Среднее время нахождения абонента в системе T вычисляется путем деления среднего количества абонентов на лямбда (Приложение B).

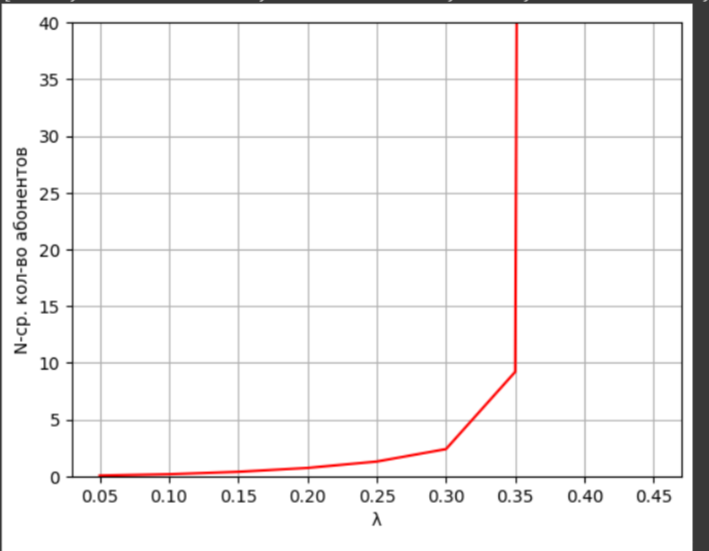
Рисунок 1 – График зависимости N от интенсивности входного потока

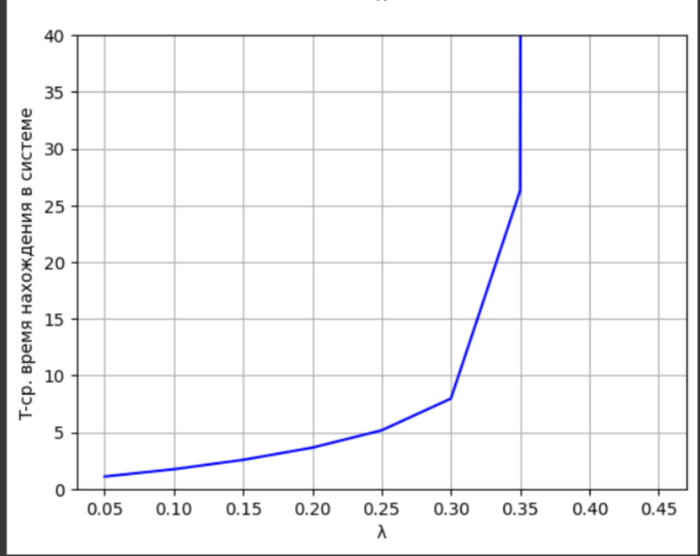
Рисунок 2 – График зависимости T от интенсивности входного потока

График отображает среднее количество абонентов в системе в зависимости от интенсивности λ. При увеличении λ до значения около 0,35 наблюдается резкое увеличение количества абонентов. Это указывает на поступление большого числа запросов, превышающих возможности системы и обработки всех запросов. В результате временной промежуток, в течение которого пользователи находятся в системе для передачи сообщений, значительно увеличивается. Это увеличение времени нахождения в системе происходит более быстро, чем увеличение количества пользователей, что свидетельствует о невозможности данной системы обеспечить эффективную работу при большом количестве пользователей.

Вывод: в ходе выполнения исследования была создана модель сети, которая способна обрабатывать сообщения только в случае, когда в определенный момент времени передается сообщение только одним абонентом. Из графика, полученного в результате, можно заключить, что эта система функционирует эффективно лишь при небольшом количестве пользователей в слоте. Однако, при достижении значения λ, приближающегося к отметке 0,35, система перестает эффективно обрабатывать сообщения и не справляется с их объемом.

Приложение А

from math import factorial, exp

from prettytable import PrettyTable

import numpy as np

N_max = 6

con = N_max + 1

matrix = [[0] * con for i in range(con)]

# Функция для построения матрицы доступа

def build_access_matrix(lambda_val, N_max):

access_matrix = np.zeros((N_max, N_max))

for Nk in range(N_max):

for Nk_plus_1 in range(N_max):

if Nk == 0:

Pk = 0

else:

Pk = lambda_val / Nk

if Nk_plus_1 == Nk + 1:

Rk = Pk - 1

else:

Rk = Pk

access_matrix[Nk][Nk_plus_1] = Rk

return access_matrix

# Значения параметра lambda (λ) с шагом 0.05

lambda_values = np.arange(0.05, 0.55, 0.05)

for lambda_val in lambda_values:

access_matrix = build_access_matrix(lambda_val, N_max)

matrix_table = PrettyTable()

matrix_table.field_names = [f'N = {i}' for i in range(N_max)]

for i, row in enumerate(access_matrix):

matrix_table.add_row([f'{value:.5f}' for value in row])

print(f"Матрица доступа для lambda = {lambda_val:.2f}:")

print(matrix_table)

print("\n")

Приложение B

from numpy import random, arange

import matplotlib.pyplot as plt

sl = 100000 # Количество слотов в сети

lambd = arange(0.05, 0.5, 0.05)

Nk = 0 # Количество пользователей в слоте

summa = 0 # Сумма количества пользователей в каждом слоте

N = [] # Массив для среднего количества абонентов

T = [] # Массив для среднего времени, для передачи сообщения одним абонентом

def function(lambd, sl, summa):

for l in lambd:

Pk = random.poisson(l, sl) # Пуассоновское распределение

# Обход каждого слота

for i in range(sl):

# Присвоение первому слоту количества пользователей

if i == 0:

Nk = Pk[i]

summa += Nk

# Обход остальных слотов

else:

try:

# Вычисление количества пользователей, собирающихся передать сообщение

Rk = random.binomial(Nk, 1 / Nk)

except:

# Если Nk = 0, то никто не передаёт сообщение, Rk=0

Rk = 0

if Rk == 1:

# Сумма при передаче одним пользователем сообщения

Nk = Nk + Pk[i] - 1

# Сумма количества пользователей в каждом слоте

summa += Nk

else:

# Сумма при количестве пользователей, передающих сообщений, большей 1

Nk = Nk + Pk[i]

summa += Nk

# Передача значений в N и T

N.append((1 / sl) * summa)

T.append(N[-1] / l)

print(T)

# Построение графика

plt.plot(lambd, N, label="N", color="red")

plt.xlabel("λ")

plt.ylabel("N-ср.кол-во.абонентов")

plt.ylim(0, 20)

plt.grid()

plt.show()

plt.plot(lambd, T, label="T", color="b")

plt.xlabel("λ")

plt.ylabel("T-ср.время нахождения в системе")

plt.ylim(0, 30)

plt.grid()

plt.show()

function(lambd, sl, summa)