
Шелест ЛР / ПиАГМ4
.docxЦель работы: реализовать и проверить на тестовом примере специальный алгоритм на графе
Вариант № 15
На рисунке 1 представлен алгоритм согласно варианту.

Рисунок 1 – Специальный алгоритм
Ход работы
Cоздан и визуализирован взвешенный ориентированный двудольный граф (Рисунок 2).
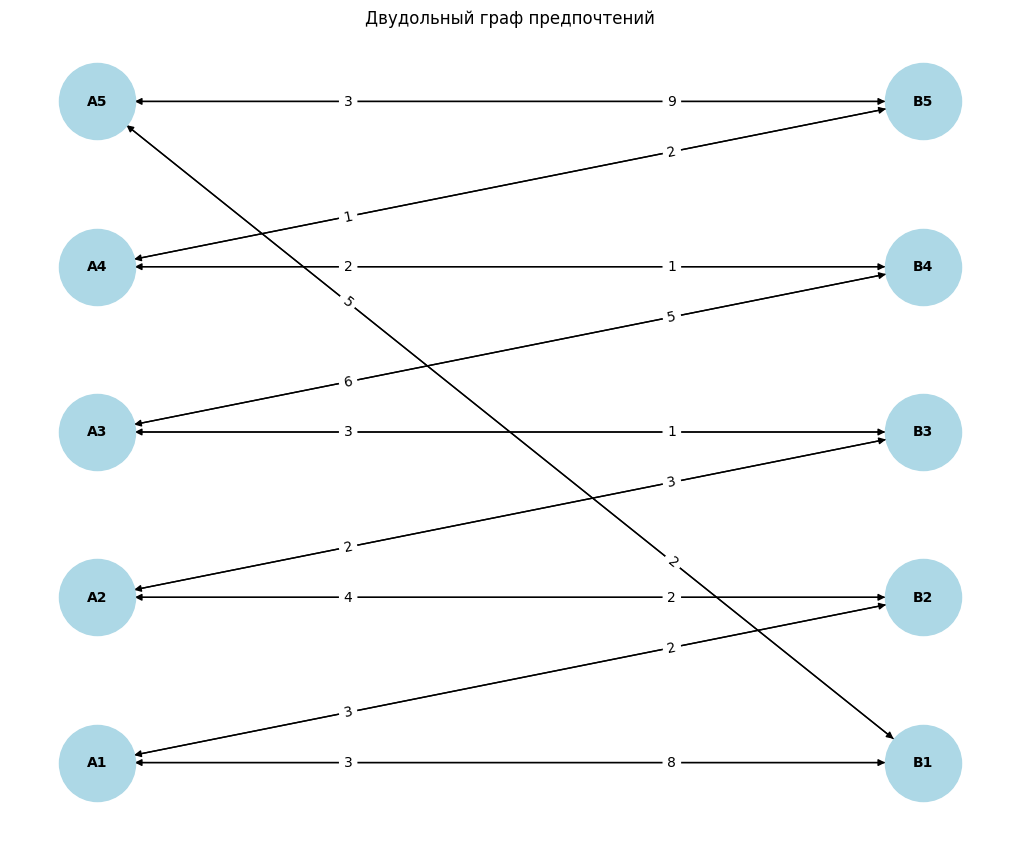
Рисунок 2 – Граф
Листинг 1 – Создание и визуализация графа
# Визуализация двудольного графа
def visualize_bipartite_graph(G):
pos = {}
men = [node for node, data in G.nodes(data=True) if data['bipartite'] == 0]
women = [node for node, data in G.nodes(data=True) if data['bipartite'] == 1]
pos.update((node, (0, i)) for i, node in enumerate(men)) # x=0 для мужчин
pos.update((node, (1, i)) for i, node in enumerate(women)) # x=1 для женщин
plt.figure(figsize=(10, 8))
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=3000, font_size=10, font_weight='bold', arrows=True)
edge_labels=dict([((u,v,),d['weight'])
for u,v,d in G.edges(data=True)])
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, label_pos=0.3, font_size=10)
plt.title("Двудольный граф предпочтений")
plt.show()
# Создание двудольного графа
G = nx.DiGraph()
men_nodes = ['A1', 'A2', 'A3', 'A4', 'A5']
women_nodes = ['B1', 'B2', 'B3', 'B4', 'B5']
for man in men_nodes:
G.add_node(man, bipartite=0)
for woman in women_nodes:
G.add_node(woman, bipartite=1)
edges = [
('A1', 'B1', 3), ('A1', 'B2', 3),
('A2', 'B2', 4), ('A2', 'B3', 2),
('A3', 'B3', 3), ('A3', 'B4', 6),
('A4', 'B4', 2), ('A4', 'B5', 1),
('A5', 'B5', 3), ('A5', 'B1', 5),
('B1', 'A1', 8), ('B1', 'A5', 2),
('B2', 'A1', 2), ('B2', 'A2', 2),
('B3', 'A2', 3), ('B3', 'A3', 1),
('B4', 'A3', 5), ('B4', 'A4', 1),
('B5', 'A4', 2), ('B5', 'A5', 9)
]
for edge in edges:
G.add_edge(edge[0], edge[1], weight=edge[2])
# Визуализация начального двудольного графа
visualize_bipartite_graph(G)
Задача о марьяже или задача о стабильных браках — математическая задача из области кооперативных игр. Требуется найти стабильные соответствия между элементами двух множеств, имеющих свои предпочтения. В более простой формулировке: составить брачные пары из женихов и невест таким образом, чтобы мужа из одной семьи и жену из другой не тянуло друг к другу сильнее, чем к своим законным супругам.
Для решения этой задачи используется алгоритм Гэйла-Шепли. Алгоритм Гейла-Шепли гарантирует нахождение стабильного паросочетания, при котором нет двух людей, которые предпочитают друг друга своим текущим партнерам.
Пошаговое выполнение алгоритма на созданном графе:
Шаг 1:
Свободные мужчины: A1, A2, A3, A4, A5.
A1 предложил B1, она свободна и приняла предложение.
Пары: A1-B1.
Шаг 2:
Свободные мужчины: A2, A3, A4, A5.
A2 предложил B2, она свободна и приняла предложение.
Пары: A1-B1, A2-B2.
Шаг 3:
Свободные мужчины: A3, A4, A5.
A3 предложил B4, она свободна и приняла предложение.
Пары: A1-B1, A2-B2, A3-B4.
Шаг 4:
Свободные мужчины: A4, A5.
A4 предложил B4, но она предпочитает своего текущего партнера A3. A4 делает следующее предложение.
Пары: A1-B1, A2-B2, A3-B4.
Шаг 5:
Свободные мужчины: A4, A5.
A4 предложил B5, она свободна и приняла предложение.
Пары: A1-B1, A2-B2, A3-B4, A4-B5.
Шаг 6:
Свободные мужчины: A5
A5 предложил B1, но она предпочитает своего текущего партнера A1. A5 делает следующее предложение.
Пары: A1-B1, A2-B2, A3-B4, A4-B5.
Шаг 7:
Свободные мужчины: A5.
A5 предложил B5, она предпочитает его текущему партнеру A4. A4 теперь свободен.
Пары: A1-B1, A2-B2, A3-B4, A5-B5.
Шаг 8:
Свободные мужчины: A4.
A4 предложил B5, но она предпочитает своего текущего партнера A5. A4 делает следующее предложение.
Пары: A1-B1, A2-B2, A3-B4, A5-B5.
Стабильные пары: A1-B1, A2-B2, A3-B4, A5-B5.
A4 больше не может сделать предложение и остается свободным.
Алгоритм был реализован средствами ЭВМ (Рисунок 3).
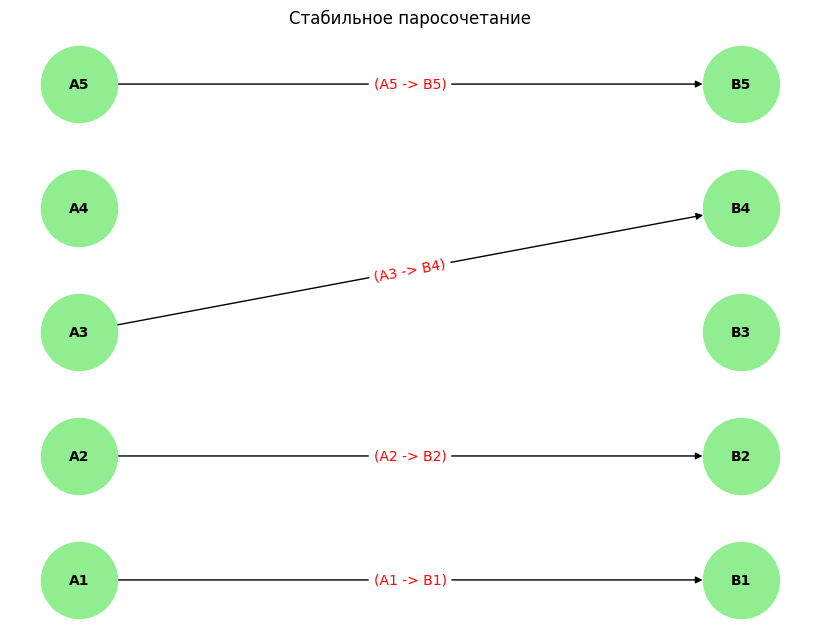
Рисунок 3 – Решение на Python
Листинг 2 – Функция алгоритма
def gale_shapley(graph, men, women):
# Начальные параметры
free_men = list(men)
engaged = {}
women_partner = {woman: None for woman in women}
men_next_proposal = {man: 0 for man in men}
men_prefs = {man: sorted(graph.neighbors(man), key=lambda x: -graph[man][x]['weight']) for man in men}
women_prefs = {woman: sorted(graph.neighbors(woman), key=lambda x: -graph[woman][x]['weight']) for woman in women}
step = 0
while free_men:
step += 1
man = free_men[0]
man_prefs = men_prefs[man]
# Если мужчина сделал предложение всем женщинам в своем списке, удаляем его из свободных
if men_next_proposal[man] >= len(man_prefs):
free_men.remove(man)
continue
# Мужчина делает предложение следующей женщине в своем списке предпочтений
woman = man_prefs[men_next_proposal[man]]
print(f"Шаг {step}:")
print(f" Свободные мужчины: {free_men}")
print(f" Предпочтения мужчин:")
for m, prefs in men_prefs.items():
print(f" {m}: {prefs} (следующий: {prefs[men_next_proposal[m]] if men_next_proposal[m] < len(prefs) else 'нет'})")
print(f" Предпочтения женщин:")
for w, prefs in women_prefs.items():
print(f" {w}: {prefs}")
if women_partner[woman] is None:
# Если женщина свободна, они обручаются
women_partner[woman] = man
engaged[man] = woman
free_men.remove(man)
print(f" {man} предложил {woman}, она свободна и приняла предложение.")
else:
# Если женщина уже обручена, она выбирает между текущим партнером и новым предложением
current_partner = women_partner[woman]
woman_prefs = women_prefs[woman]
if woman_prefs.index(man) < woman_prefs.index(current_partner):
# Женщина предпочитает нового партнера
engaged.pop(current_partner)
women_partner[woman] = man
engaged[man] = woman
free_men.remove(man)
free_men.append(current_partner)
print(f" {man} предложил {woman}, она предпочитает его текущему партнеру {current_partner}. {current_partner} теперь свободен.")
else:
# Женщина отвергает новое предложение
men_next_proposal[man] += 1
print(f" {man} предложил {woman}, но она предпочитает своего текущего партнера {current_partner}. {man} делает следующее предложение.")
print("Пары:",engaged)
print("\n")
return engaged
Полный код программы представлен в Листинге 3.
Вывод: в ходе выполнения практической работы была решена задача о марьяже с помощью алгоритма Гейла-Шепли. Этот алгоритм был реализован средствами языка программирования Python, был осуществлен вывод изначального взвешенного ориентированного двудольного графа, применение алгоритма на граф и вывод получившихся стабильных пар. Алгоритм Гейла-Шепли используется для нахождения стабильного выбора.
Листинг 3 – Полный код программы
import matplotlib.pyplot as plt
import networkx as nx
def gale_shapley(graph, men, women):
# Начальные параметры
free_men = list(men)
engaged = {}
women_partner = {woman: None for woman in women}
men_next_proposal = {man: 0 for man in men}
men_prefs = {man: sorted(graph.neighbors(man), key=lambda x: -graph[man][x]['weight']) for man in men}
women_prefs = {woman: sorted(graph.neighbors(woman), key=lambda x: -graph[woman][x]['weight']) for woman in women}
step = 0
while free_men:
step += 1
man = free_men[0]
man_prefs = men_prefs[man]
# Если мужчина сделал предложение всем женщинам в своем списке, удаляем его из свободных
if men_next_proposal[man] >= len(man_prefs):
free_men.remove(man)
continue
# Мужчина делает предложение следующей женщине в своем списке предпочтений
woman = man_prefs[men_next_proposal[man]]
print(f"Шаг {step}:")
print(f" Свободные мужчины: {free_men}")
print(f" Предпочтения мужчин:")
for m, prefs in men_prefs.items():
print(f" {m}: {prefs} (следующий: {prefs[men_next_proposal[m]] if men_next_proposal[m] < len(prefs) else 'нет'})")
print(f" Предпочтения женщин:")
for w, prefs in women_prefs.items():
print(f" {w}: {prefs}")
if women_partner[woman] is None:
# Если женщина свободна, они обручаются
women_partner[woman] = man
engaged[man] = woman
free_men.remove(man)
print(f" {man} предложил {woman}, она свободна и приняла предложение.")
else:
# Если женщина уже обручена, она выбирает между текущим партнером и новым предложением
current_partner = women_partner[woman]
woman_prefs = women_prefs[woman]
if woman_prefs.index(man) < woman_prefs.index(current_partner):
# Женщина предпочитает нового партнера
engaged.pop(current_partner)
women_partner[woman] = man
engaged[man] = woman
free_men.remove(man)
free_men.append(current_partner)
print(f" {man} предложил {woman}, она предпочитает его текущему партнеру {current_partner}. {current_partner} теперь свободен.")
else:
# Женщина отвергает новое предложение
men_next_proposal[man] += 1
print(f" {man} предложил {woman}, но она предпочитает своего текущего партнера {current_partner}. {man} делает следующее предложение.")
print("Пары:",engaged)
print("\n")
return engaged
# Визуализация двудольного графа
def visualize_bipartite_graph(G):
pos = {}
men = [node for node, data in G.nodes(data=True) if data['bipartite'] == 0]
women = [node for node, data in G.nodes(data=True) if data['bipartite'] == 1]
pos.update((node, (0, i)) for i, node in enumerate(men)) # x=0 для мужчин
pos.update((node, (1, i)) for i, node in enumerate(women)) # x=1 для женщин
plt.figure(figsize=(10, 8))
nx.draw(G, pos, with_labels=True, node_color='lightblue', node_size=3000, font_size=10, font_weight='bold', arrows=True)
edge_labels=dict([((u,v,),d['weight'])
for u,v,d in G.edges(data=True)])
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, label_pos=0.3, font_size=10)
plt.title("Двудольный граф предпочтений")
plt.show()
# Создание двудольного графа
G = nx.DiGraph()
men_nodes = ['A1', 'A2', 'A3', 'A4', 'A5']
women_nodes = ['B1', 'B2', 'B3', 'B4', 'B5']
for man in men_nodes:
G.add_node(man, bipartite=0)
for woman in women_nodes:
G.add_node(woman, bipartite=1)
edges = [
('A1', 'B1', 3), ('A1', 'B2', 3),
('A2', 'B2', 4), ('A2', 'B3', 2),
('A3', 'B3', 3), ('A3', 'B4', 6),
('A4', 'B4', 2), ('A4', 'B5', 1),
('A5', 'B5', 3), ('A5', 'B1', 5),
('B1', 'A1', 8), ('B1', 'A5', 2),
('B2', 'A1', 2), ('B2', 'A2', 2),
('B3', 'A2', 3), ('B3', 'A3', 1),
('B4', 'A3', 5), ('B4', 'A4', 1),
('B5', 'A4', 2), ('B5', 'A5', 9)
]
for edge in edges:
G.add_edge(edge[0], edge[1], weight=edge[2])
# Визуализация начального двудольного графа
visualize_bipartite_graph(G)
# Выполнение алгоритма Гейла-Шепли
result = gale_shapley(G, men_nodes, women_nodes)
print("\nСтабильные пары:", result)
# Визуализация стабильного паросочетания
def visualize_matching(G, matching):
matching_graph = nx.DiGraph()
for man in men_nodes:
matching_graph.add_node(man, bipartite=0)
for woman in women_nodes:
matching_graph.add_node(woman, bipartite=1)
for man, woman in matching.items():
matching_graph.add_edge(man, woman)
pos = {}
pos.update((node, (0, i)) for i, node in enumerate(men_nodes)) # x=0 для мужчин
pos.update((node, (1, i)) for i, node in enumerate(women_nodes)) # x=1 для женщин
plt.figure(figsize=(8, 6))
nx.draw(matching_graph, pos, with_labels=True, node_color='lightgreen', node_size=3000, font_size=10, font_weight='bold', arrows=True)
edge_labels = {(man, woman): f"({man} -> {woman})" for man, woman in matching.items()}
nx.draw_networkx_edge_labels(matching_graph, pos, edge_labels=edge_labels, font_color='red')
plt.title("Стабильное паросочетание")
plt.show()
visualize_matching(G, result)
