Шелест ЛР / ПиАГМ3

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				М.Н. Шелест
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

СЛУЧАЙНЫЕ ГРАФЫ И ИХ СВОЙСТВА

по курсу: ПОСТРОЕНИЕ И АНАЛИЗ ГРАФОВЫХ МОДЕЛЕЙ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
				подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: рассмотреть различные подходы к генерации случайных графов в ЭВМ. Провести анализ свойств созданных графов.

Вариант № 15

На рисунках 1, 2 представлены алгоритм и задание согласно варианту.

Рисунок 1 – Алгоритм создания графа

Рисунок 2 – Задание

Ход работы

Написана и выполнена функция для создания графа, граф визуализирован (Рисунок 3).

Рисунок 3 – Граф общего вида

Листинг 1 – Создание и визуализация графа

def create_graph(N, M, R):

# Генерируем случайные координаты для N точек внутри квадратной области размером M x M

points = np.random.uniform(0, M, size=(N, 2))

# Создаем матрицу смежности

adjacency_matrix = np.zeros((N, N))

# Заполняем матрицу смежности

for i in range(N):

for j in range(i + 1, N):

if np.linalg.norm(abs(points[i] - points[j])) < R:

adjacency_matrix[i, j] = 1

adjacency_matrix[j, i] = 1 # Убедимся, что матрица симметрична

# Создаем граф из матрицы смежности

G = nx.from_numpy_array(adjacency_matrix)

# Добавляем позиции вершин для отображения

pos = {i: points[i] for i in range(N)}

nx.set_node_attributes(G, pos, 'pos')

return G

# Параметры

N = 100 # число вершин

p = 0.05

# Вычисляем размер области M и расстояние R

M = np.sqrt(N) / 2

R = np.sqrt(p * M**2 / np.pi)

# Создаем и отображаем граф

G = create_graph(N, M, R)

components = nx.number_connected_components(G)

plt.figure(figsize=(12, 12))

plt.title(f'N = {N}, M = {round(M, 2)}, R = {round(R, 2)}, p = {round(p,2)}, число компонент: {components}')

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, node_size=50, with_labels=False)

plt.show()

Реализована функция получения спектра степеней графа, спектр степеней графа представлен в виде гистограммы (Рисунок 4).

Рисунок 4 – Гистограмма

Листинг 2 – Вычисление спектра степеней графа

def degree_spectrum(G):

# Получаем степени вершин графа

degrees = [d for n, d in G.degree()]

# Сортируем степени по возрастанию

degrees.sort()

return degrees

# Получаем спектр степеней для графа G

degree_spec = degree_spectrum(G)

# Построение гистограммы спектра степеней

plt.hist(degree_spec, bins=range(min(degree_spec), max(degree_spec) + 1, 1), edgecolor='black')

plt.title('Гистограмма спектра степеней графа')

plt.xlabel('Степень вершины')

plt.ylabel('Частота')

plt.grid(True)

plt.show()

Для каждого значения M ( ) создан и визуализирован граф, построена гистограмма спектра степеней графа (Рисунок 5).

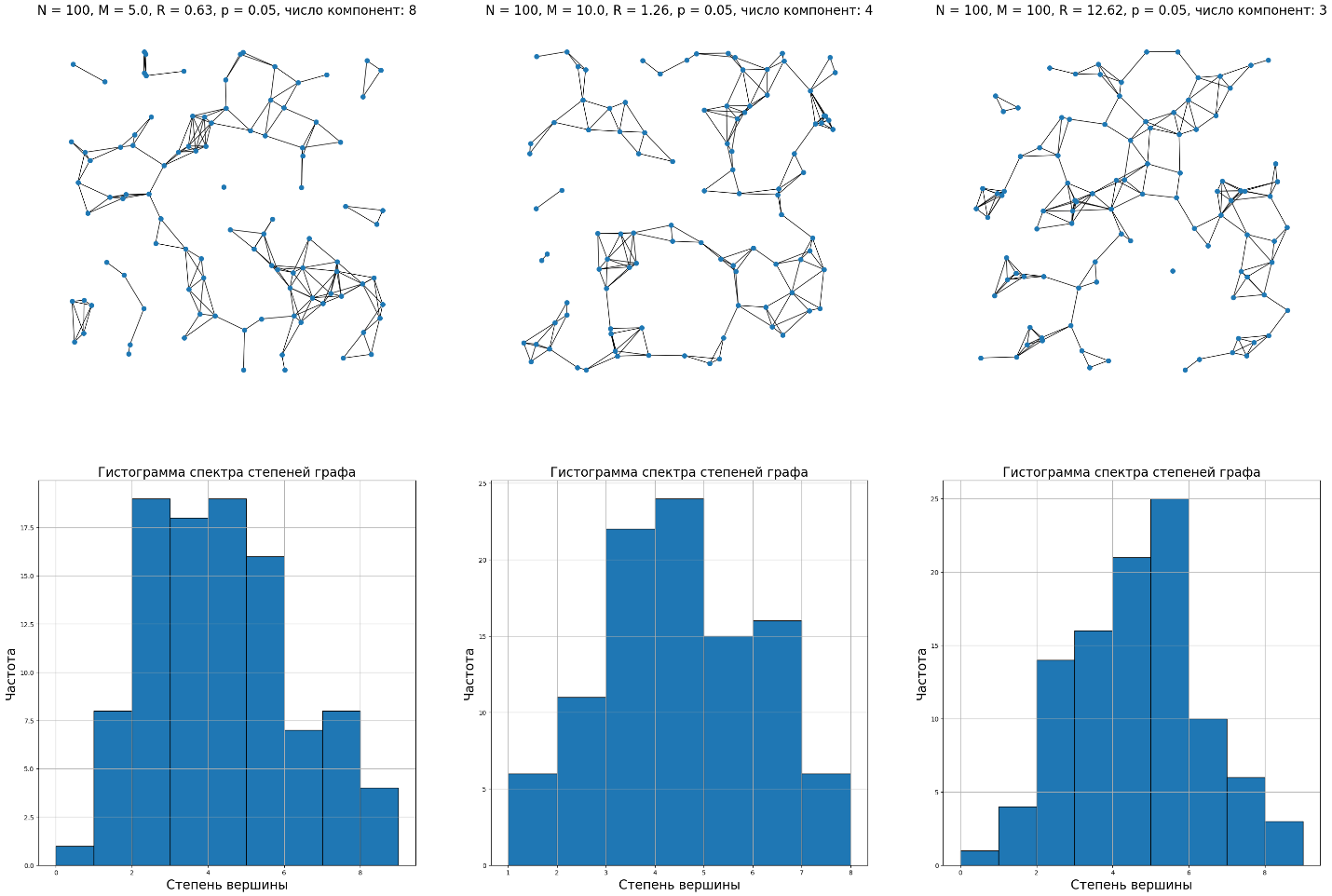
Рисунок 5 – Графы и гистограммы для каждого значения M

Листинг 3 – Построение графов и гистограмм

N = 100

M_values = [np.sqrt(N)/2, np.sqrt(N), N]

p = 0.05

for i, M in enumerate(M_values):

# Параметр R для текущего значения p

R = np.sqrt(p * M**2 / np.pi)

# Создаем и отображаем граф

G = create_graph(N, M, R)

components = nx.number_connected_components(G)

plt.figure(1, figsize = (36, 24))

plt.subplot(2, 3, i+1)

plt.title(f'N = {N}, M = {round(M, 2)}, R = {round(R, 2)}, p = {round(p,2)}, число компонент: {components}', fontsize = 20)

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, node_size=50, with_labels=False)

# Получаем спектр степеней для графа G

degree_spec = degree_spectrum(G)

# Построение гистограммы спектра степеней

plt.subplot(2, 3, i+4)

plt.hist(degree_spec, bins=range(min(degree_spec), max(degree_spec) + 1, 1), edgecolor='black')

plt.title('Гистограмма спектра степеней графа', fontsize = 20)

plt.xlabel('Степень вершины', fontsize = 20)

plt.ylabel('Частота', fontsize = 20)

plt.grid(True)

plt.show()

Построен график зависимости среднего количества компонент графа от p для каждого значения M (Рисунок 6 - 8).

Рисунок 6 – График, M = 5

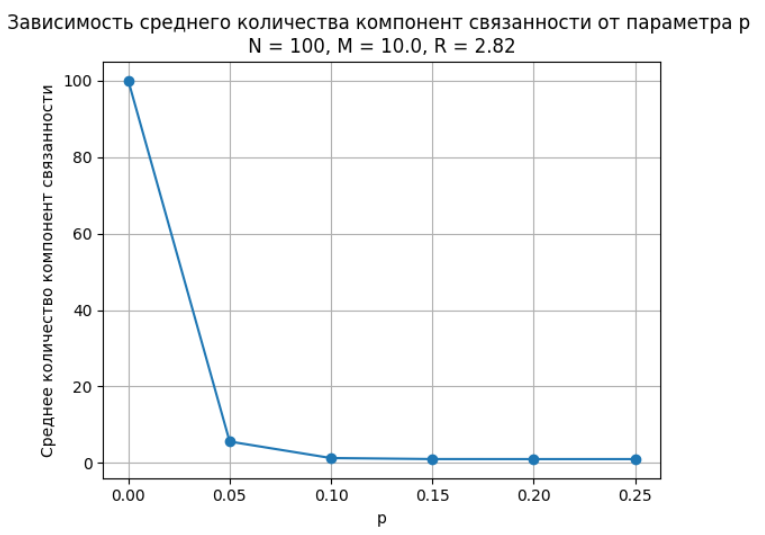
Рисунок 7 – График, M = 10

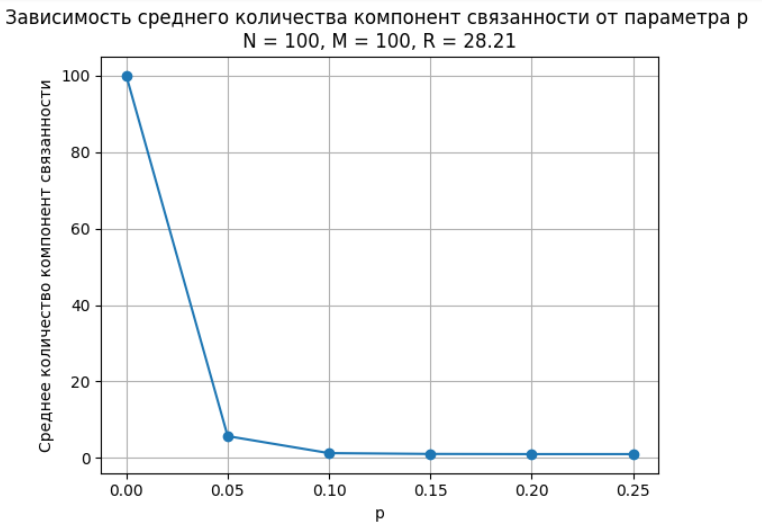
Рисунок 8 – График, M = 100

Листинг 4 – Вычисление зависимости среднего количества компонент связности от p

# Задаем значения параметров

p_values = np.arange(0, 0.3, 0.05)

N = 100

M_values = [np.sqrt(N)/2, np.sqrt(N), N]

avg_edges_M = []

for i, M in enumerate(M_values):

# Создаем пустые списки для хранения среднего количества компонент связанности

avg_components = []

avg_edges = []

for j, p_val in enumerate(p_values):

# Параметр R для текущего значения p

R = np.sqrt(p_val * M**2 / np.pi)

# Сгенерируем несколько графов для текущего значения p и посчитаем количество компонент связанности

num_components = []

num_edges = []

for _ in range(100): # Генерируем 10 графов для усреднения

G = create_graph(N, M, R)

num_components_val = nx.number_connected_components(G)

num_components.append(num_components_val)

num_edges_val = G.number_of_edges()

num_edges.append(num_edges_val)

plt.figure(i, figsize = (36, 30))

plt.suptitle(f"N = {N}, M = {round(M, 2)}", fontsize = 50)

plt.subplot(2, 3, j+1)

plt.title(f'p = {p_val.round(2)}, R = {R.round(2)}, компонент: {num_components_val}', fontsize = 30)

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, with_labels=True, node_size = 150, node_color='lightblue', font_size=10)

# Среднее количество компонент связанности для текущего значения p

avg_components.append(np.mean(num_components))

avg_edges.append(np.mean(num_edges))

plt.show()

avg_edges_M.append(avg_edges)

# Построим график зависимости среднего количества компонент связанности от параметра p

plt.plot(p_values, avg_components, marker='o')

plt.title(f'Зависимость среднего количества компонент связанности от параметра p \n N = {N}, M = {round(M, 2)}, R = {R.round(2)} ')

plt.xlabel('p')

plt.ylabel('Среднее количество компонент связанности')

plt.grid(True)

plt.show()

# Построим график зависимости среднего количества ребер от параметра p

ticks = []

plt.figure(figsize = (15, 30))

for avg_edges in avg_edges_M:

plt.plot(p_values, avg_edges, marker='o', linewidth=0.5, markersize = 2)

ticks+=avg_edges

plt.title(f'Зависимость среднего количества ребер от параметра p')

plt.xlabel('p')

plt.ylabel('Среднее количество ребер')

plt.grid(True)

plt.yticks(ticks)

plt.show()

По графикам видно, что с увеличением p число компонент свзяности стремится к 1. Более наглядно это увидеть можно на рисунке 8.

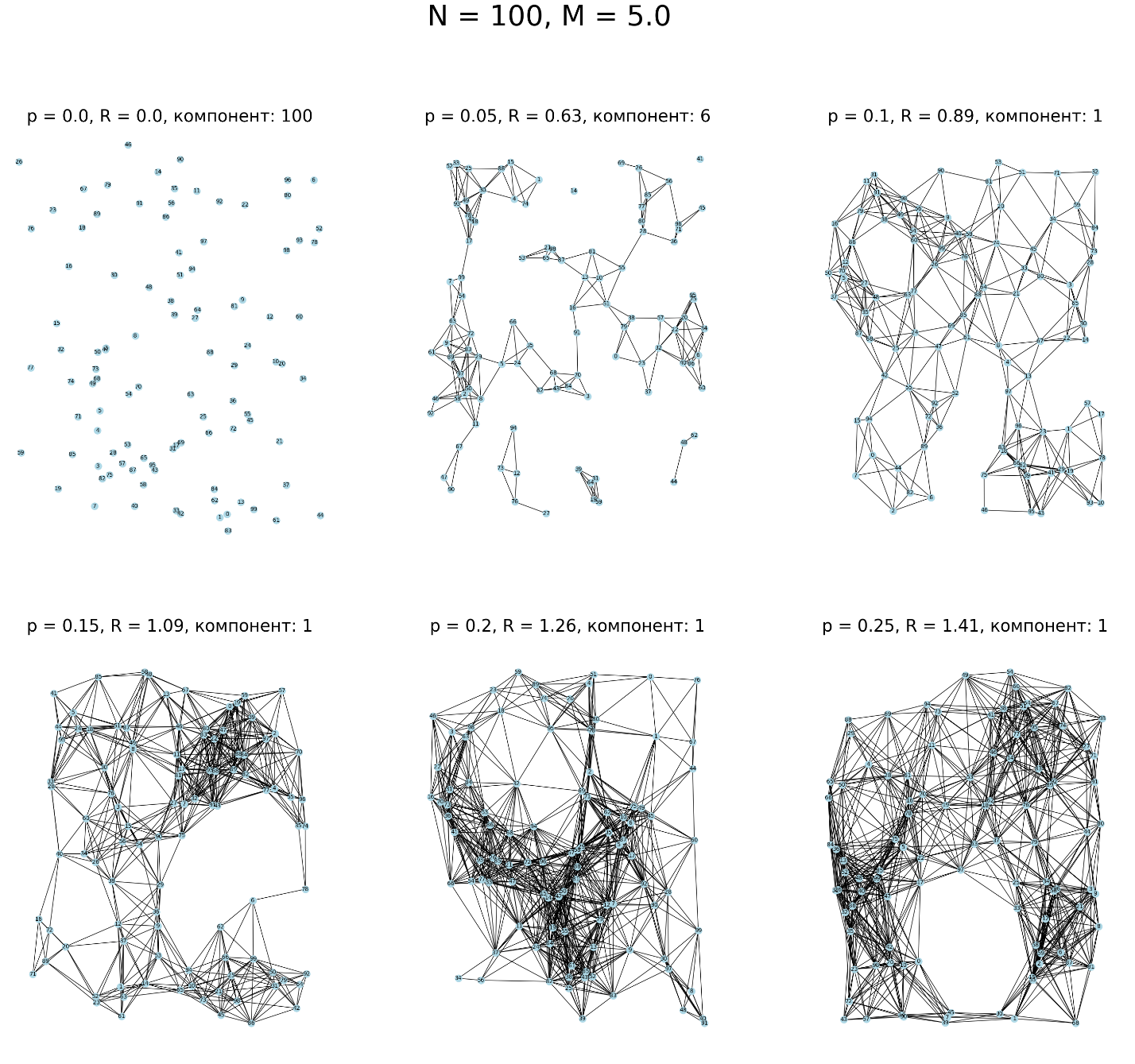
Рисунок 8 – Увеличение параметра p

Вывод: в ходе выполнения лабораторной работы реализована функция для создания графа общего вида с условием для соединения вершин, функция для вычисления спектра степеней графа и построена гистограмма спектра степеней. Вычислена и визуализирована зависимость среднего количества компонент связности графа от p для разного числа вершин. Графики показали, что с ростом p, количество компонент связности стремится к 1. Подобные графы используются в эпидемиологии для моделирования распространения болезней.

Листинг 5 – Полный код программы

import numpy as np

import networkx as nx

import matplotlib.pyplot as plt

np.random.seed(1)

def create_graph(N, M, R):

# Генерируем случайные координаты для N точек внутри квадратной области размером M x M

points = np.random.uniform(0, M, size=(N, 2))

# Создаем матрицу смежности

adjacency_matrix = np.zeros((N, N))

# Заполняем матрицу смежности

for i in range(N):

for j in range(i + 1, N):

if np.linalg.norm(abs(points[i] - points[j])) < R:

adjacency_matrix[i, j] = 1

adjacency_matrix[j, i] = 1 # Убедимся, что матрица симметрична

# Создаем граф из матрицы смежности

G = nx.from_numpy_array(adjacency_matrix)

# Добавляем позиции вершин для отображения

pos = {i: points[i] for i in range(N)}

nx.set_node_attributes(G, pos, 'pos')

return G

# Параметры

N = 100 # число вершин

p = 0.05

# Вычисляем размер области M и расстояние R

M = np.sqrt(N) / 2

R = np.sqrt(p * M**2 / np.pi)

# Создаем и отображаем граф

G = create_graph(N, M, R)

components = nx.number_connected_components(G)

plt.figure(figsize=(12, 12))

plt.title(f'N = {N}, M = {round(M, 2)}, R = {round(R, 2)}, p = {round(p,2)}, число компонент: {components}')

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, node_size=50, with_labels=False)

plt.show()

# Функция поиска спектра степеней графа

def degree_spectrum(G):

# Получаем степени вершин графа

degrees = [d for n, d in G.degree()]

# Сортируем степени по возрастанию

degrees.sort()

return degrees

# Получаем спектр степеней для графа G

degree_spec = degree_spectrum(G)

# Построение гистограммы спектра степеней

plt.hist(degree_spec, bins=range(min(degree_spec), max(degree_spec) + 1, 1), edgecolor='black')

plt.title('Гистограмма спектра степеней графа')

plt.xlabel('Степень вершины')

plt.ylabel('Частота')

plt.grid(True)

plt.show()

N = 100

M_values = [np.sqrt(N)/2, np.sqrt(N), N]

p = 0.05

for i, M in enumerate(M_values):

# Параметр R для текущего значения p

R = np.sqrt(p * M**2 / np.pi)

# Создаем и отображаем граф

G = create_graph(N, M, R)

components = nx.number_connected_components(G)

plt.figure(1, figsize = (36, 24))

plt.subplot(2, 3, i+1)

plt.title(f'N = {N}, M = {round(M, 2)}, R = {round(R, 2)}, p = {round(p,2)}, число компонент: {components}', fontsize = 20)

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, node_size=50, with_labels=False)

# Получаем спектр степеней для графа G

degree_spec = degree_spectrum(G)

# Построение гистограммы спектра степеней

plt.subplot(2, 3, i+4)

plt.hist(degree_spec, bins=range(min(degree_spec), max(degree_spec) + 1, 1), edgecolor='black')

plt.title('Гистограмма спектра степеней графа', fontsize = 20)

plt.xlabel('Степень вершины', fontsize = 20)

plt.ylabel('Частота', fontsize = 20)

plt.grid(True)

plt.show()

# Задаем значения параметров

p_values = np.arange(0, 0.3, 0.05)

N = 100

M_values = [np.sqrt(N)/2, np.sqrt(N), N]

avg_edges_M = []

for i, M in enumerate(M_values):

# Создаем пустые списки для хранения среднего количества компонент связанности

avg_components = []

avg_edges = []

for j, p_val in enumerate(p_values):

# Параметр R для текущего значения p

R = np.sqrt(p_val * M**2 / np.pi)

# Сгенерируем несколько графов для текущего значения p и посчитаем количество компонент связанности

num_components = []

num_edges = []

for _ in range(100): # Генерируем 10 графов для усреднения

G = create_graph(N, M, R)

num_components_val = nx.number_connected_components(G)

num_components.append(num_components_val)

num_edges_val = G.number_of_edges()

num_edges.append(num_edges_val)

plt.figure(i, figsize = (36, 30))

plt.suptitle(f"N = {N}, M = {round(M, 2)}", fontsize = 50)

plt.subplot(2, 3, j+1)

plt.title(f'p = {p_val.round(2)}, R = {R.round(2)}, компонент: {num_components_val}', fontsize = 30)

pos = nx.get_node_attributes(G, 'pos')

nx.draw(G, pos, with_labels=True, node_size = 150, node_color='lightblue', font_size=10)

# Среднее количество компонент связанности для текущего значения p

avg_components.append(np.mean(num_components))

avg_edges.append(np.mean(num_edges))

plt.show()

avg_edges_M.append(avg_edges)

# Построим график зависимости среднего количества компонент связанности от параметра p

plt.plot(p_values, avg_components, marker='o')

plt.title(f'Зависимость среднего количества компонент связанности от параметра p \n N = {N}, M = {round(M, 2)}, R = {R.round(2)} ')

plt.xlabel('p')

plt.ylabel('Среднее количество компонент связанности')

plt.grid(True)

plt.show()

# Построим график зависимости среднего количества ребер от параметра p

ticks = []

plt.figure(figsize = (15, 30))

for avg_edges in avg_edges_M:

plt.plot(p_values, avg_edges, marker='o', linewidth=0.5, markersize = 2)

ticks+=avg_edges

plt.title(f'Зависимость среднего количества ребер от параметра p')

plt.xlabel('p')

plt.ylabel('Среднее количество ребер')

plt.grid(True)

plt.yticks(ticks)

plt.show()