
Шелест ЛР / ПиАГМ2ДопЗадание
.docxДополнительное задание: доработать алгоритм с учетом взвешенности графа. При сжатии вершины, новое соединение имеет вес равный сумме смежных ребер для удаляемой вершины, если данной связи не существовало ранее. Иначе выбирается минимум из существующей связи и суммы смежных ребер для удаляемой вершины. Построить график зависимости отношения полученного в результате сжатия количества вершин к исходному количеству вершин от размера решетки. В результате должен быть код с комментариями, скриншот исходного графа и результата сжатия. График по отношению количества вершин.
Функция гомеоморфного сжатия графа дополнена для работы с весами ребер.
Листинг 1 – Функция гомеоморфного сжатия
def homeomorphic_compression(G):
# Создание копии графа, чтобы не изменять исходный граф
compressed = G.copy()
# Флаг изменений в графе
changed = True
while changed:
changed = False
# Перебор всех вершин в графе
for node in list(compressed.nodes):
# Проверка, является ли степень вершины равна 2
if compressed.degree(node) == 2:
# Получение соседей вершины
neighbors = list(compressed.neighbors(node))
neighbor1, neighbor2 = neighbors[0], neighbors[1]
# Получение весов смежных ребер
edge_weight_node_to_neighbor1 = compressed[node][neighbor1]['weight']
edge_weight_node_to_neighbor2 = compressed[node][neighbor2]['weight']
# Проверка, есть ли ребро между соседями
if compressed.has_edge(neighbor1, neighbor2):
# Если ребро есть, то его вес равен минимуму из суммы весов смежных ребер и веса существующего ребра
edge_weight = min((edge_weight_node_to_neighbor1 + edge_weight_node_to_neighbor2), compressed[neighbor1][neighbor2]['weight'])
compressed[neighbor1][neighbor2]['weight'] = edge_weight
else:
# Если ребра между соседями нет, оно добавляется, вес равен сумме смежных ребер
edge_weight = edge_weight_node_to_neighbor1 + edge_weight_node_to_neighbor2
compressed.add_edge(neighbor1, neighbor2, weight = edge_weight)
# Удаление вершины из графа
compressed.remove_node(node)
# Фиксация изменения в графе
changed = True
break # Начало цикла заново, так как граф был изменен во время итерации
# Возврат сжатого графа
return compressed
Написана функция для добавления случайных весов ребрам.
Листинг 2 – Функция для добавления случайных весов ребрам
def add_random_weights(G):
# Цикл по всем ребрам
for edge in G.edges():
# Генерация веса между 1 и 10
weight = np.random.randint(low=1, high=10)
# Добавление веса ребру
G.edges[edge]['weight'] = weight
# Возврат взвешенного графа
return G
Построен график зависимости отношения количества ребер графа после сжатия к исходному от размера решетки (Рисунок 1).
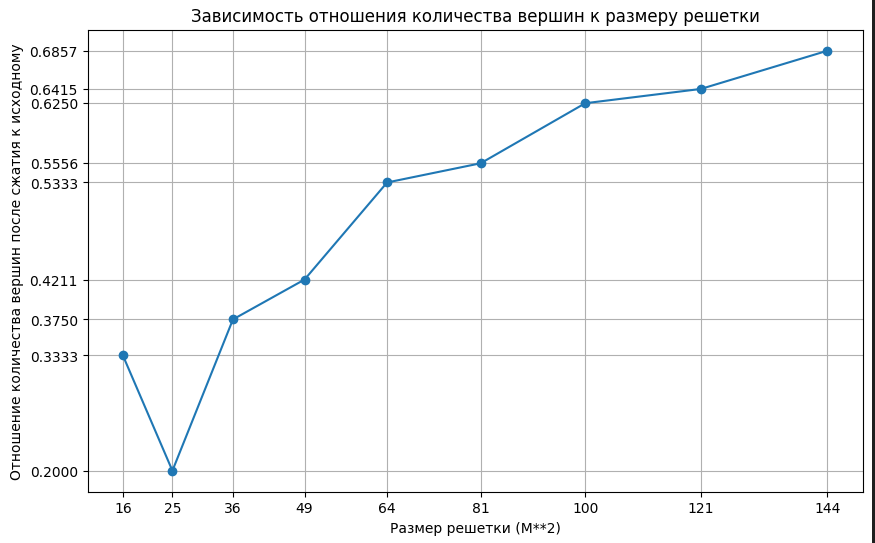
Рисунок 1 – График зависимости
Листинг 3 – Построение графика
# Диапазон значений M для построения решетки M^2 на M^2
M_values = np.arange(4, 13, 1)
# Пустые массивы для размера решетки и отношения
x = []
y = []
# Цикл для измерения среднего времени выполнения сжатия для каждого значения M
for M in M_values:
# Получение матрицы смежности
matrix = create_adjacency_matrix(M)
# Создание графа
G = nx.Graph(matrix)
# Выполнение гомеоморфного сжатия
compressed_G = homeomorphic_compression(G)
# Получение количества вершин в сжатом и исходном графах
n_nodes_compressed = compressed_G.number_of_nodes()
n_nodes = G.number_of_nodes()
# Занесение размера решетки и отношения в массивы x и y соответственно
x.append(M**2)
y.append(n_nodes_compressed/n_nodes)
# Построение графика
plt.figure(figsize=(10, 6))
plt.plot(x, y, marker='o')
plt.xticks(x)
plt.yticks(y)
plt.title('Зависимость отношения количества вершин к размеру решетки')
plt.xlabel('Размер решетки (M**2)')
plt.ylabel('Отношение количества вершин после сжатия к исходному')
plt.grid(True)
plt.show()
Провал на графике при размере решетки 25 связан с тем, что при размере решетки 16 и 25 в исходном графе количество вершин 6 и 10 соответственно, а в сжатых 2 вершины (Рисунок 2 – 4).
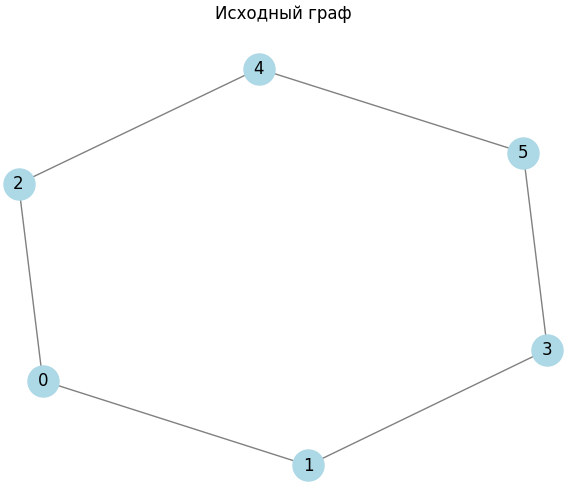
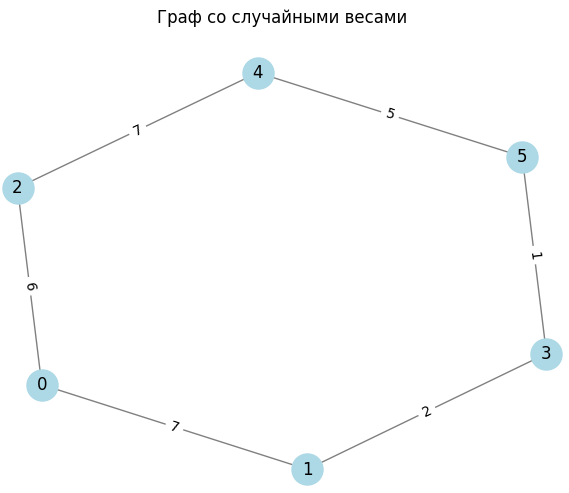
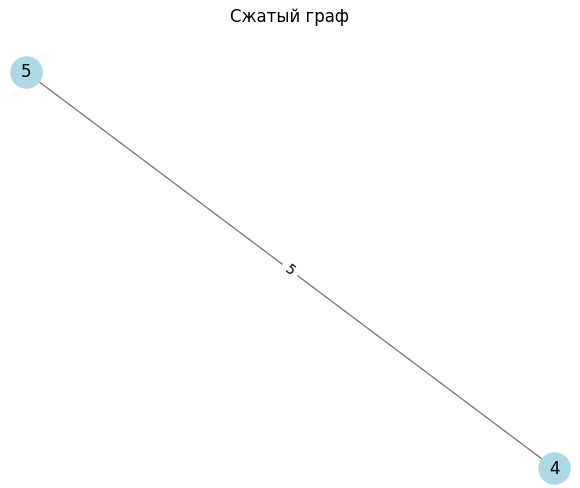
Рисунок 2 – Размер решетки 16

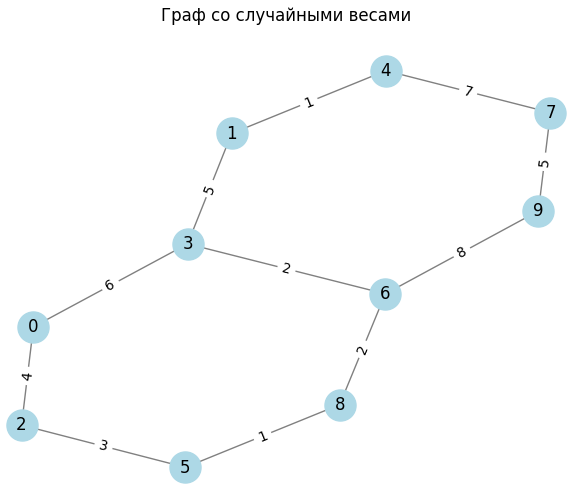
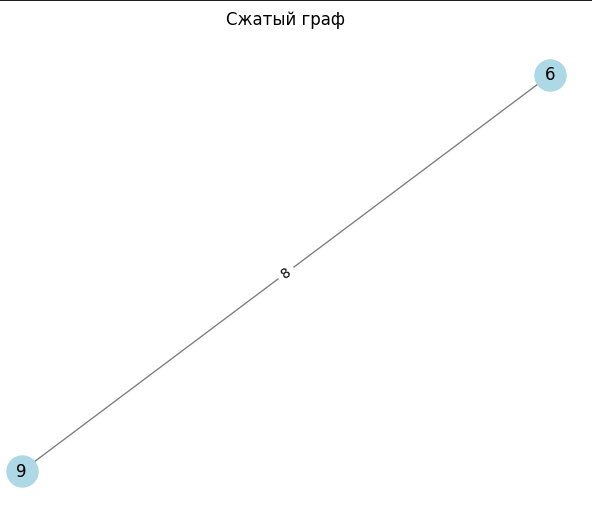
Рисунок 3 – Размер решетки 25
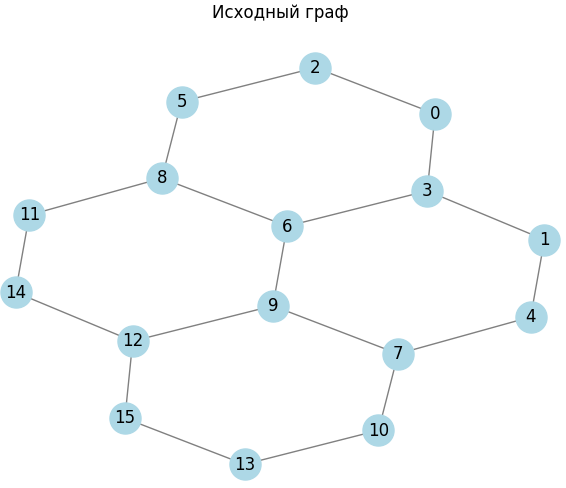
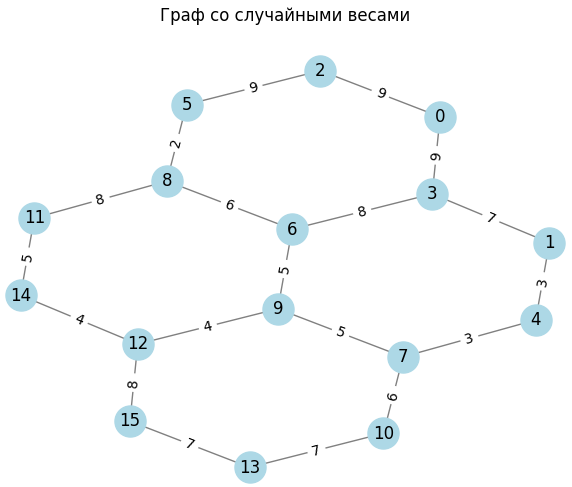
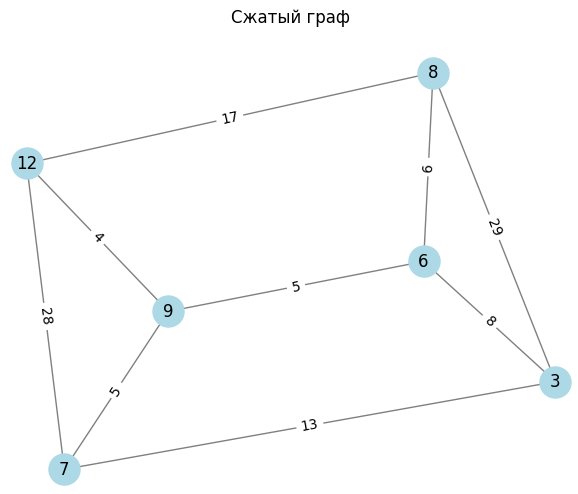
Рисунок 4 – Размер решетки 36
Листинг 4 – Визуализация графов
# Задание значения M
M = 6
# Получение матрицы смежности
matrix = create_adjacency_matrix(M)
# Создание графа
G = nx.Graph(matrix)
# Получение позиций вершин для визуализации
positions = get_nodes_postitions(G)
# Визуализация исходного графа
draw_graph(G, positions, 'Исходный граф')
# Добавление случайных весов ребрам
G = add_random_weights(G)
# Визуализация взвешенного графа
draw_weighted_graph(G, positions, "Граф со случайными весами")
# Выполнение гомеоморфного сжатия
compressed_G = homeomorphic_compression(G)
# Визуализация сжатого графа
draw_weighted_graph(compressed_G, nx.spectral_layout(G), "Сжатый граф")
Листинг 5 – Полный код программы
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
# Фиксация рандома для воспроизводимости результатов
np.random.seed(2)
# Функция для создания матрицы смежности графа правильной шестиугольной решетки
def create_adjacency_matrix(M):
# Создание нулевой квадратной матрицы Matrix размера M^2 на M^2
Matrix = np.zeros((M**2, M**2))
# Создание ребер между вершинами
for V in range(M**2):
R = V // M # Вычисление номера строки
C = V % M # Вычисление номера столбца
# Если вершина удовлетворяет условиям для создания ребер
if (R % 4 == 0 and C % 2 == 1) or (R % 4 == 2 and C % 2 == 0):
# Добавление ребер с верхними и нижними вершинами
if R > 0:
Matrix[V][V - M] = Matrix[V - M][V] = 1 # Ребро с верхней вершиной
if R < (M - 1) and C < (M - 1):
Matrix[V][V + M + 1] = Matrix[V + M + 1][V] = 1 # Ребро с нижней правой вершиной
if R < (M - 1) and C > 0:
Matrix[V][V + M - 1] = Matrix[V + M - 1][V] = 1 # Ребро с нижней левой вершиной
# Удаление лишних вершин
row_sums = np.sum(Matrix, axis=1) # Вычисление суммы по строкам
while np.any(row_sums < 2):
index = np.argmin(row_sums) # Индекс строки с минимальной суммой
Matrix = np.delete(Matrix, index, axis=0) # Удаление строки
Matrix = np.delete(Matrix, index, axis=1) # Удаление столбца
row_sums = np.sum(Matrix, axis=1) # Обновление суммы по строкам
return Matrix
def homeomorphic_compression(G):
# Создание копии графа, чтобы не изменять исходный граф
compressed = G.copy()
# Флаг изменений в графе
changed = True
while changed:
changed = False
# Перебор всех вершин в графе
for node in list(compressed.nodes):
# Проверка, является ли степень вершины равна 2
if compressed.degree(node) == 2:
# Получение соседей вершины
neighbors = list(compressed.neighbors(node))
neighbor1, neighbor2 = neighbors[0], neighbors[1]
# Получение весов смежных ребер
edge_weight_node_to_neighbor1 = compressed[node][neighbor1]['weight']
edge_weight_node_to_neighbor2 = compressed[node][neighbor2]['weight']
# Проверка, есть ли ребро между соседями
if compressed.has_edge(neighbor1, neighbor2):
# Если ребро есть, то его вес равен минимуму из суммы весов смежных ребер и веса существующего ребра
edge_weight = min((edge_weight_node_to_neighbor1 + edge_weight_node_to_neighbor2), compressed[neighbor1][neighbor2]['weight'])
compressed[neighbor1][neighbor2]['weight'] = edge_weight
else:
# Если ребра между соседями нет, оно добавляется, вес равен сумме смежных ребер
edge_weight = edge_weight_node_to_neighbor1 + edge_weight_node_to_neighbor2
compressed.add_edge(neighbor1, neighbor2, weight = edge_weight)
# Удаление вершины из графа
compressed.remove_node(node)
# Фиксация изменения в графе
changed = True
break # Начало цикла заново, так как граф был изменен во время итерации
# Возврат сжатого графа
return compressed
# Функция для генерации расположения вершин
def get_nodes_postitions(G):
pos = nx.kamada_kawai_layout(G)
return pos
# Функция для визуализации графа
def draw_graph(G, positions, title):
nx.draw(G, pos = positions, with_labels=True, node_color='lightblue', edge_color='gray', node_size=500)
plt.title(title)
plt.show()
# Функция для добавления случайных весов
def add_random_weights(G):
# Цикл по всем ребрам
for edge in G.edges():
# Генерация веса между 1 и 10
weight = np.random.randint(low=1, high=10)
# Добавление веса ребру
G.edges[edge]['weight'] = weight
# Возврат взвешенного графа
return G
# Функция для визуализации взвешенного графа
def draw_weighted_graph(G, positions, title):
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw(G, pos=positions, with_labels=True, node_color='lightblue', edge_color='gray', node_size=500)
nx.draw_networkx_edge_labels(G, positions, edge_labels=edge_labels)
plt.title(title)
plt.show()
# Задание значения M
M = 6
# Получение матрицы смежности
matrix = create_adjacency_matrix(M)
# Создание графа
G = nx.Graph(matrix)
# Получение позиций вершин для визуализации
positions = get_nodes_postitions(G)
# Визуализация исходного графа
draw_graph(G, positions, 'Исходный граф')
# Добавление случайных весов ребрам
G = add_random_weights(G)
# Визуализация взвешенного графа
draw_weighted_graph(G, positions, "Граф со случайными весами")
# Выполнение гомеоморфного сжатия
compressed_G = homeomorphic_compression(G)
# Визуализация сжатого графа
draw_weighted_graph(compressed_G, nx.spectral_layout(G), "Сжатый граф")
# Диапазон значений M для построения решетки M^2 на M^2
M_values = np.arange(4, 13, 1)
# Пустые массивы для размера решетки и отношения
x = []
y = []
# Цикл для измерения среднего времени выполнения сжатия для каждого значения M
for M in M_values:
# Получение матрицы смежности
matrix = create_adjacency_matrix(M)
# Создание графа
G = nx.Graph(matrix)
# Выполнение гомеоморфного сжатия
compressed_G = homeomorphic_compression(G)
# Получение количества вершин в сжатом и исходном графах
n_nodes_compressed = compressed_G.number_of_nodes()
n_nodes = G.number_of_nodes()
# Занесение размера решетки и отношения в массивы x и y соответственно
x.append(M**2)
y.append(n_nodes_compressed/n_nodes)
# Построение графика
plt.figure(figsize=(10, 6))
plt.plot(x, y, marker='o')
plt.xticks(x)
plt.yticks(y)
plt.title('Зависимость отношения количества вершин к размеру решетки')
plt.xlabel('Размер решетки (M**2)')
plt.ylabel('Отношение количества вершин после сжатия к исходному')
plt.grid(True)
plt.show()
