Шелест ЛР / ПиАГМ1

Цель работы:

Изучение представления графов в ЭВМ при помощи матрицы смежности, множества пар вершин и массива структур. Визуализация графов.

Ход работы:

Вариант 15 представлен на рисунке 1.

Рисунок 1 – Граф по варианту 15

В таблице 1 представлена Матрица Смежности графа.

Таблица 1 – Матрица Смежности

	Kindergarten	School	College	University	Work	Pension
Kindergarten	0	7	0	0	0	0
School	0	0	9	11	9	0
College	0	0	0	3	3	0
University	0	0	0	0	6	0
Work	0	0	0	0	0	40
Pension	0	0	0	0	0	0

Для создания списка ребер в графе создана функция, принимающая матрицу смежности и возвращающая два списка кортежей: с номерами вершин и весом грани, с названиями вершин и весом. Для создания списков функция проходит циклами по матрице до тех пор, пока не встретит ненулевой элемент, заносит в кортеж соответствующие значения (Рисунок 2).

Листинг:

def edges_list(matrix):

edges = []

named_edges = []

for i in range(len(matrix)):

for j in range(len(matrix[i])):

if matrix[i][j] != 0:

edges.append((i, j, matrix[i][j]))

named_edges.append((nodes[i], nodes[j], matrix[i][j]))

return edges, named_edges

edges, named_edges = edges_list(adjacency_matrix)

print("\n","Рёбра")

for edge in edges:

print(edge, nodes[edge[0]],"->",nodes[edge[1]])

print("Size =",sys.getsizeof(edges),"bytes")

print("\n","Рёбра с Именами")

for edge in named_edges:

print(edge)

print("Size =",sys.getsizeof(named_edges),"bytes")

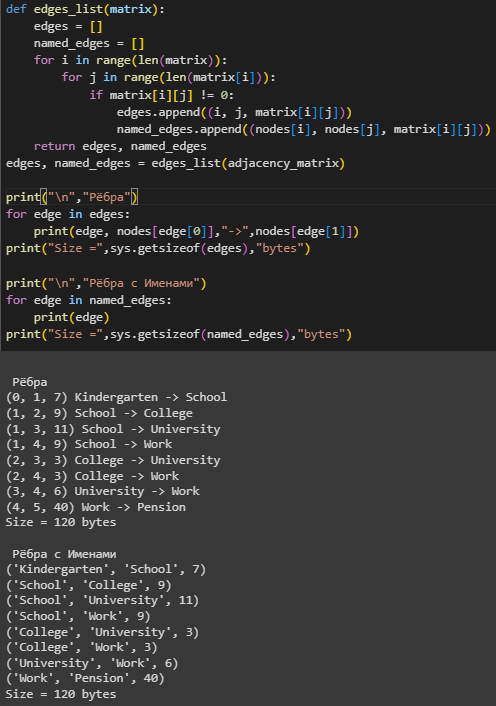
Рисунок 2 – Построение списка ребер

Написана функция для удобного представления информации о графе. На вход подается матрица смежности и названия вершин, возвращается датафрейм с информацией о графе. С помощью циклов функция проходит по матрице и добавляет в массивы детей и родителей каждой вершины, затем аналогично находит веса ребер. После того, как значения для родителей и детей найдены, они складываются чтобы найти значения для всех соседей. В конце вся полученная информация переводится в формат строки и заносится в датафрейм. (Рисунок 3)

Листинг:

def graph_to_records(matrix, node_labels):

records = []

for i, label in enumerate(node_labels):

children = [j for j, edge in enumerate(matrix[i]) if edge != 0]

parents = [j for j, row in enumerate(matrix) if row[i] != 0]

children_edge_weights = [matrix[i][j] for j in children]

parents_edge_weights = [matrix[j][i] for j in parents]

neighbors = children+parents

neighbors_edge_weights = children_edge_weights+parents_edge_weights

record = {

'Node': label,

'Children': ', '.join(str(node_labels[j]) for j in children),

'Children Count': len(children),

'Children Edge Weights': ', '.join(str(weight) for weight in children_edge_weights),

'Parents': ', '.join(str(node_labels[j]) for j in parents),

'Parents Count': len(parents),

'Parents Edge Weights': ', '.join(str(weight) for weight in parents_edge_weights),

'Neighbors': ', '.join(str(node_labels[j]) for j in neighbors),

'Neighbors Count': len(neighbors),

'Neighbors Edge Weights': ', '.join(str(weight) for weight in neighbors_edge_weights)

}

records.append(record)

df = pd.DataFrame(records)

return df

df = graph_to_records(adjacency_matrix, nodes)

print("Size =",sys.getsizeof(df),"bytes")

df

Рисунок 3 – Датафрейм

Для матрицы смежности написаны функции для нахождения всех соседей заданной вершины, ответа, образует ли заданная последовательность вершин цепь, номеров вершин, сумма весов инцидентных ребер которых больше

заданной величины, количества ребер в графе (Рисунок 4 - 7).

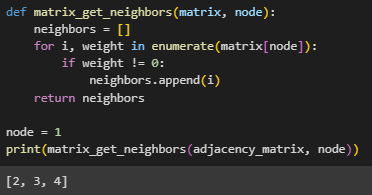Рисунок 4 – Нахождение соседей

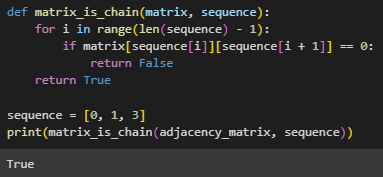
Рисунок 5 – Является ли последовательность цепью

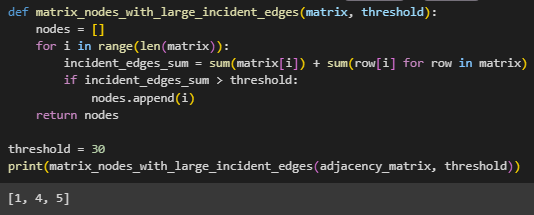
Рисунок 6 – Сумма инцидентных ребер

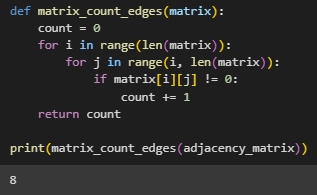
Рисунок 7 – Количество ребер

Аналогично написаны функции для остальных представлений графа.

Реализована визуализация графа с помощью библиотек networkx и matplotlib (Рисунок 8).

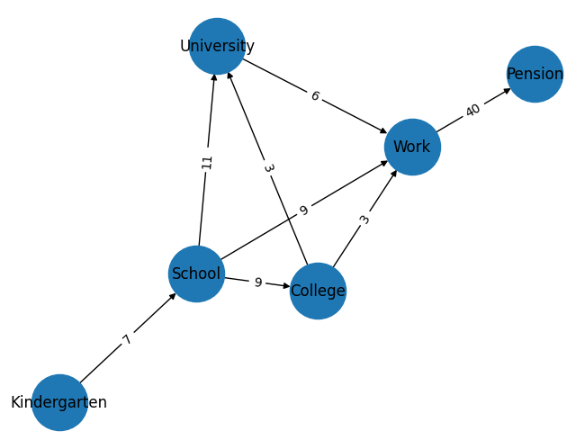
Рисунок 8 - Визуализация графа

С помощью библиотеки time проведено тестирование на время выполнения функций для каждого представления графа (Рисунок 9).

Рисунок 9 – Время для Матрицы Смежности

Рисунок 10 – Время для Списка Ребер

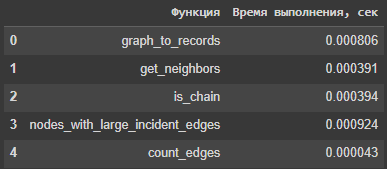
Рисунок 11 – Время для Датафрейма

С помощью библиотеки sys выведен размер каждого представления графа (Рисунок 12).

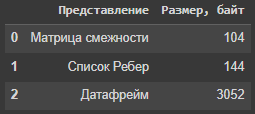
Рисунок 12 – Размеры представлений

Вывод:

В ходе выполнения практической работы граф был представлен в различных форматах, созданы функции для определения числа соседей вершин, числа ребер и т.д. По результатам тестирования на время выполнения функций лучше всего показала себя матрица смежности, значения списка ребер незначительно отличаются в худшую сторону, в то время как работа с датафреймом стала самой медленной. По результатам анализа размера представлений самый маленький размер у Матрицы смежности, самый крупный – у датафрейма.