ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				В.В. Боженко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

РАСПОЗНАВАНИЕ ОБРАЗОВ

по курсу: МАШИННОЕ ОБУЧЕНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы: обучить нейронную сеть Хопфилда распознавать образ

Ход работы

Вариант 15

На рисунке 1 представлен вариант задания.

Рисунок 1 – Вариант задания

Импортированы библиотеки numpy, matplotlib и random (Рисунок 2).

Рисунок 2 – Импорт библиотек

Эталонные изображения представлены в виде матриц размером 5 на 6 (Рисунок 3).

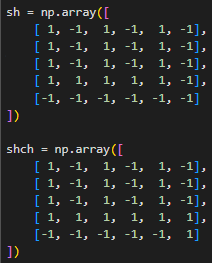
Рисунок 3 – Представление эталонных образов в виде матриц

Создана функция для визуализации изображений. На вход поступают названия изображений, матрицы по которым строятся изображения, размеры сетки изображений x и y (Рисунок 4).

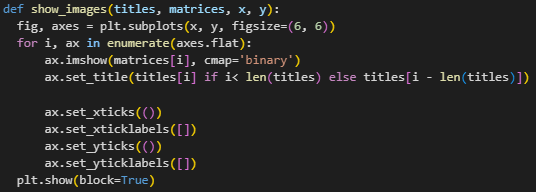
Рисунок 4 – Функция для визуализации

Визуализированы созданные матрицы (Рисунок 5).

Рисунок 5 – Эталонные изображения

Написана функция для добавления шума в матрицу. На вход поступает матрица, вероятность шума (по умолчанию 0.1). Создается копия матрицы, чтобы не изменять эталонную, далее с помощью циклов происходит перебор всех значений и, если случайное число оказывается меньше порога шума, изменение значения. Функция возвращает зашумленную матрицу. Созданы и визуализированы две зашумленные матрицы (Рисунок 6).

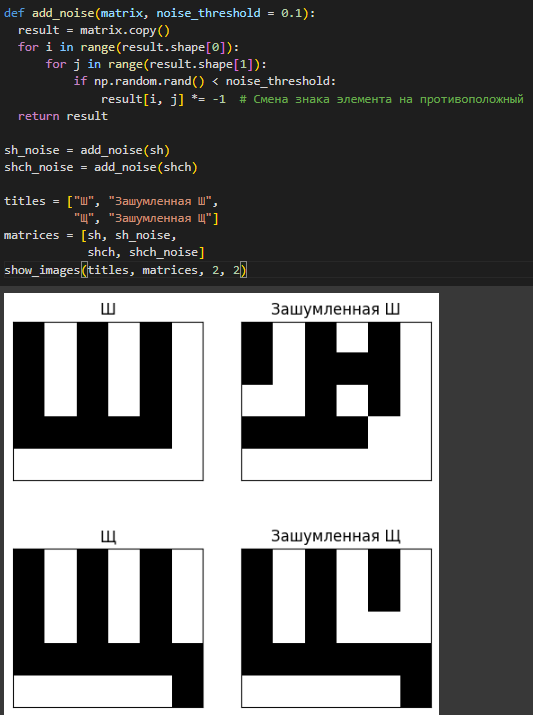
Рисунок 6 – Генерация и визуализация шума

Написаны функции для реализации сети Хопфилда и вычисления весов для неё. Вычислены веса для эталонных матриц (Рисунок 7).

Функция compute_hopfield_weights берет список образов и превращает их в матрицу весов. Матрица весов – это то, что определяет, как сильно связаны между собой разные части образа. Чтобы создать эту матрицу, просматривается каждый образ в отдельности, преобразуется его в одномерный массив и умножается сам на себя таким образом, чтобы получить матрицу. Затем эта матрица добавляется к общей матрице весов. В итоге, матрица весов содержит информацию о всех образах одновременно.

Функция hopfield_weights берет зашумленное изображение и пытается восстановить оригинальный образ, используя матрицу весов. Она делает это, постоянно обновляя зашумленное изображение: каждый пиксель (нейрон) обновляется на основе того, как он связан с другими пикселями в матрице весов. Функция продолжает обновлять изображение указанное число раз или до тех пор, пока изображение больше не меняется, пытаясь приблизиться к одному из запомненных образов. В результате функция возвращает восстановленное изображение, которое должно быть очищено от шума.

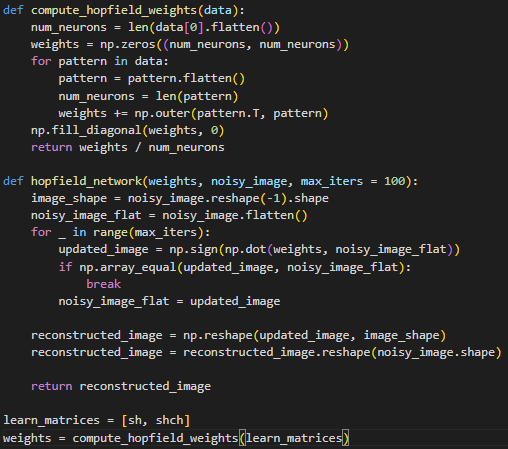
Рисунок 7 – Функции для вычисления весов и выполнения предсказания

Выполнены и визуализированы предсказания букв (Рисунок 8).

Рисунок 8 – Выполнение и визуализация предсказаний

Написана функция для тестирования предсказаний (Рисунок 9), на вход поступает матрица эталонного изображения, порог шума, число тестов, переменная, определяющая нужно ли осуществлять вывод, возвращает массив со значениями ошибки восстановления.

В ходе цикла повторений происходит генерация зашумленного изображения, выполнение предсказания, вычисление ошибки восстановления и занесение её в массив, если необходимо, вывод изображений и характеристик.

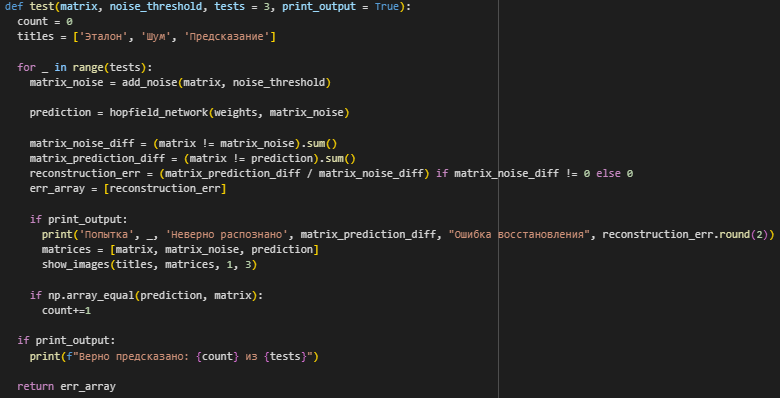
Рисунок 9 – Функция тестирования

Выполнены предсказания букв c порогом шума 0.2 (Рисунок 10, 11).

Рисунок 10 – Предсказания Ш

Рисунок 11 – Предсказания Щ

Вероятность верного предсказания при пороге шума 0.2 составила 55% и 63% соответственно.

Построен график зависимости ошибки восстановления от степени зашумления изображений (Рисунок 12).

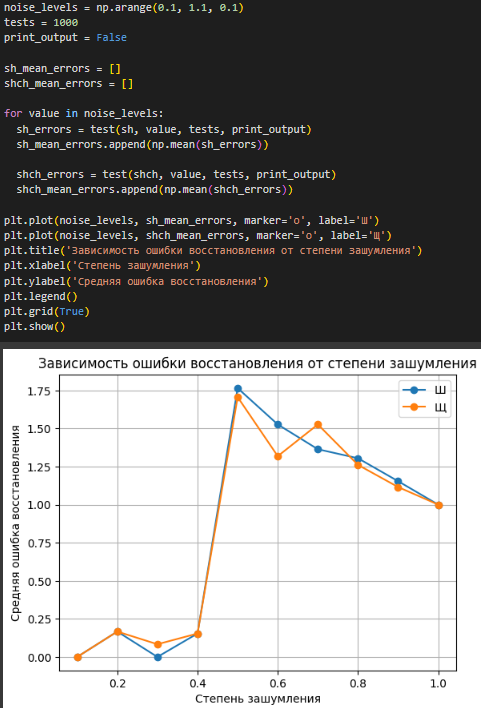
Рисунок 12 – График зависимости

По графику видно, что при значении порога шума 0.5 и выше, предсказанное изображение отличается от эталонного сильнее чем зашумленное. Это исходит из того, что в результате предсказания с порогом шума 0.5 очень часто попадается изображение обратное эталонному.

После увеличения максимального числа обновлений изображения в сети Хопфилда с 100 до 10000, удалось добиться снижения средней ошибки восстановления и пик графика немного сдвинулся право (Рисунок 13).

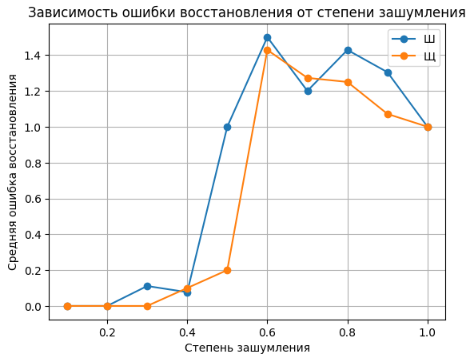
Рисунок 13 – График после увеличения числа обновлений

Ссылка на Google Colab:

Вывод:

В ходе выполнения лабораторной работы созданы матрицы эталонных изображений, написаны функции для визуализации, зашумления изображений, вычисления матрицы весов и восстановления зашумленных изображений с помощью сети Хопфилда. Из 100 попыток буква «Ш» была верно предсказана 55 раз, «Щ» была верно предсказана 63 раза. Вычислена ошибка восстановления, построен график её зависимости от степени зашумления. Для улучшения качества предсказаний было увеличено максимальное число обновлений изображения в сети Хопфилда, это привело к снижению средней ошибки восстановления.