М4

ГУАП

КАФЕДРА № 41

ОТЧЕТ

ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель Е.К. Григорьев

^{должность, уч. степень, звание подпись, дата инициалы, фамилия}

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ № 4

СТАТИСТИЧЕСКИЙ АНАЛИЗ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

по курсу: МОДЕЛИРОВАНИЕ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. № ^{подпись, дата инициалы, фамилия}

Санкт-Петербург 2024

1 Цель работы

Получить навыки обработки выборочных данных средствами MATLAB/GNU Octave.

2 Ход работы

Вариант 15

Выполнение первой части задания представлено на рисунках 1 – 3.

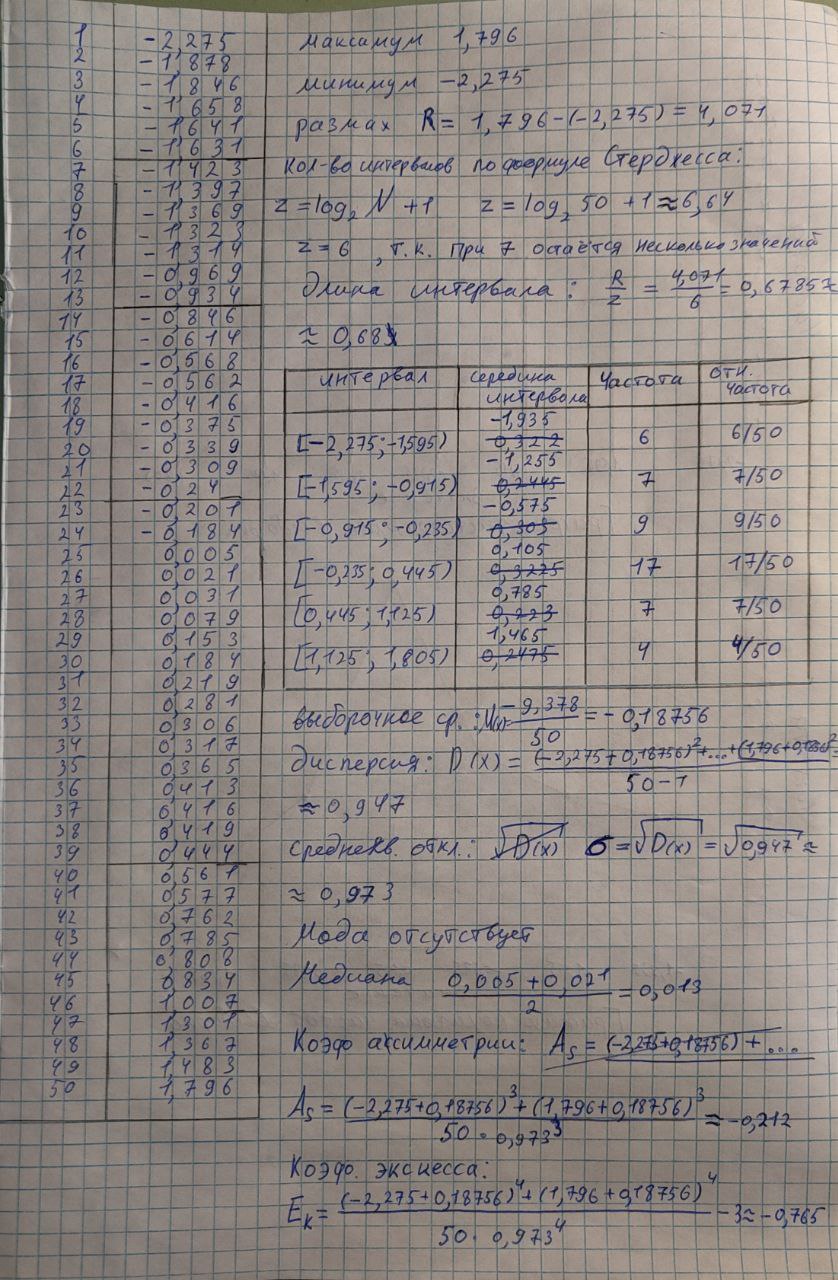
Рисунок 1 – Разделение на интервалы и вычисление метрик

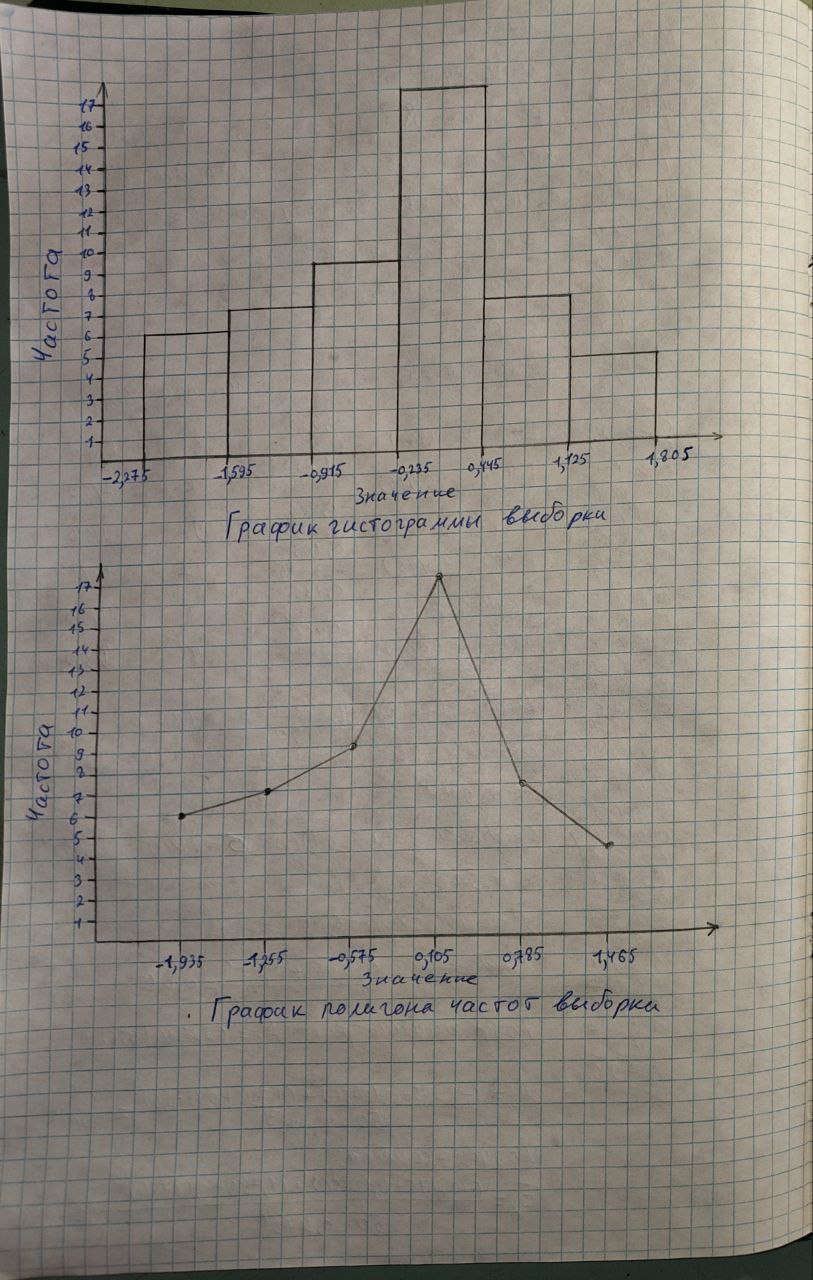
Рисунок 2 – Графики гистограммы выборки и полигона частот выборки

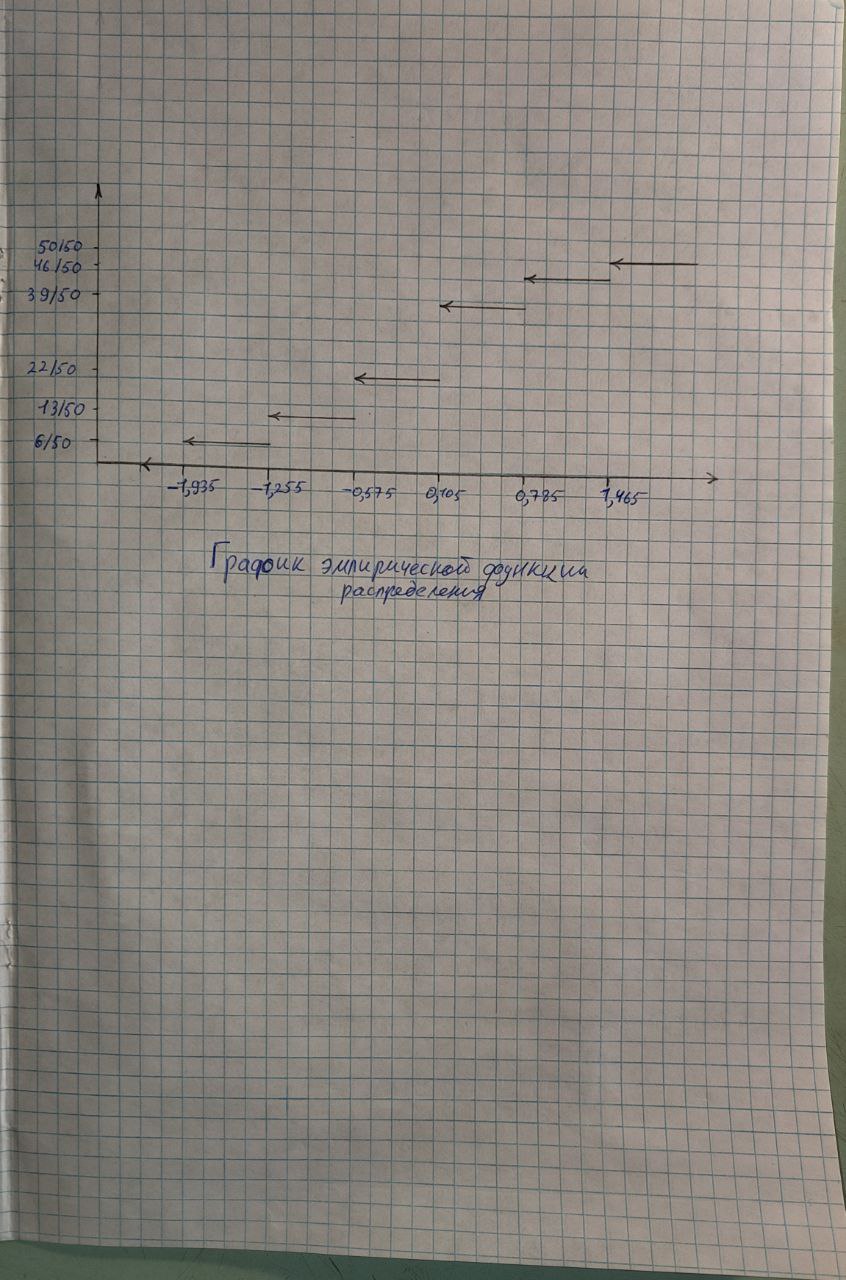
Рисунок 3 – График эмпирической функции распределения

На рисунке 4 представлено вычисление метрик в MS Excel.

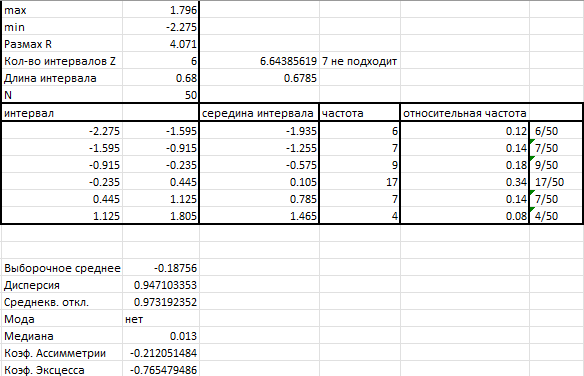
Рисунок 4 – Метрики в MS Excel

Отрицательный коэффициент асимметрии указывает на слабую левостороннюю асимметрию.

Коэффициент эксцесса меньше нуля, что говорит о более плоском, по сравнению с нормальным, распределении.

Гистограмма показывает, что большинство значений сконцентрированы около центра, с плавным уменьшением количества значений к краям. Это указывает на симметричность распределения.

График плотности вероятности имеет чёткий пик, который плавно уменьшается к обеим сторонам. Это подтверждает, что распределение близко к нормальному.

График эмпирической функции распределения показывает непрерывное возрастание по мере увеличения значений, типичное для нормального распределения.

Исходя из графиков, можно сделать вывод, что распределение очень близко к нормальному распределению. Это подтверждается формой гистограммы и графика плотности вероятности, а также симметрией данных вокруг среднего значения и характерными значениями коэффициентов асимметрии и эксцесса.

Выполнение второй части задания представлено на рисунках 5 – 10.

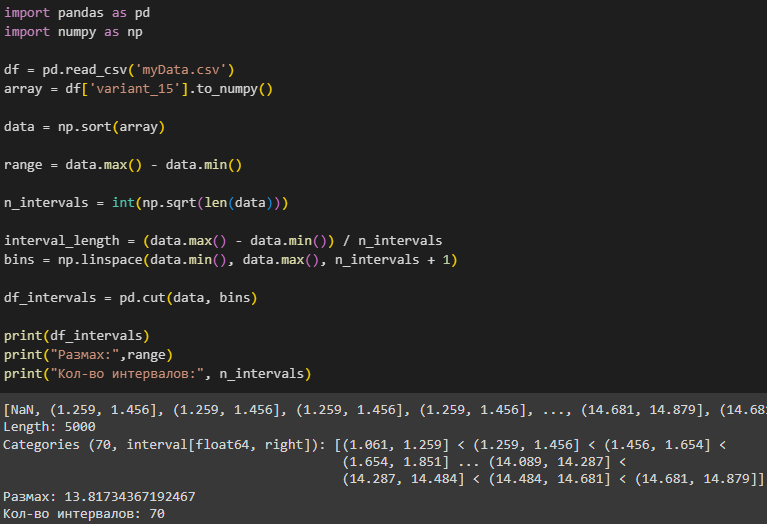
Рисунок 5 – Импорт данных и определение размаха выборки и количества интервалов

Рисунок 6 – График гистограммы выборки

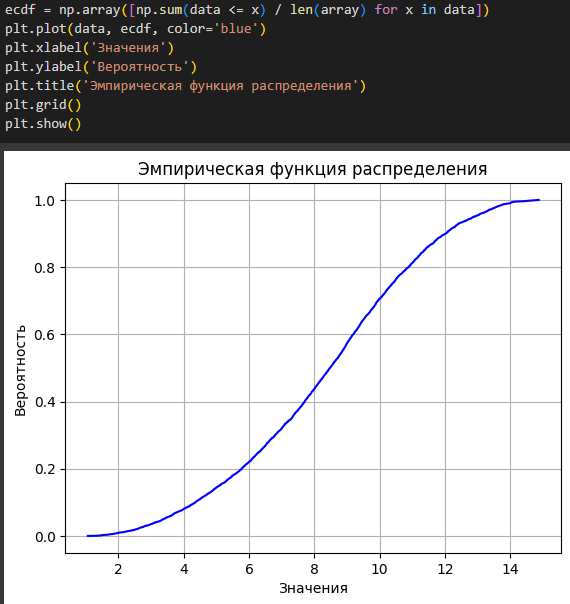
Рисунок 7 – График эмпирической функции распределения

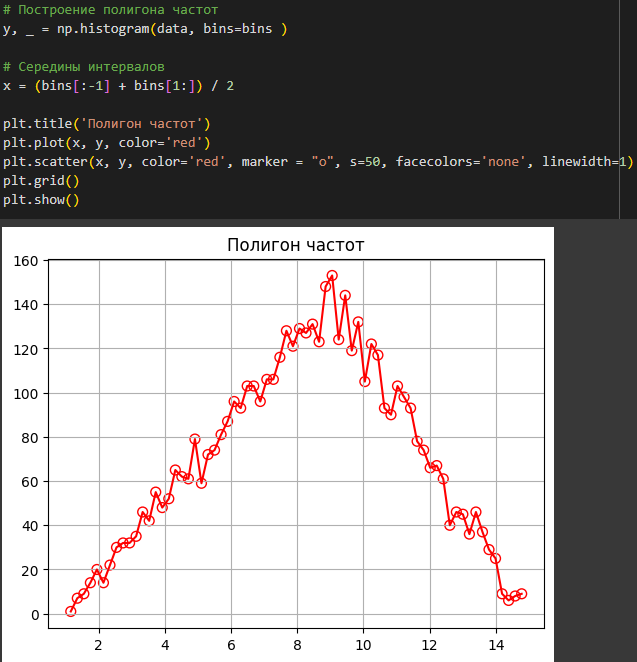
Рисунок 8 – График полигона частот

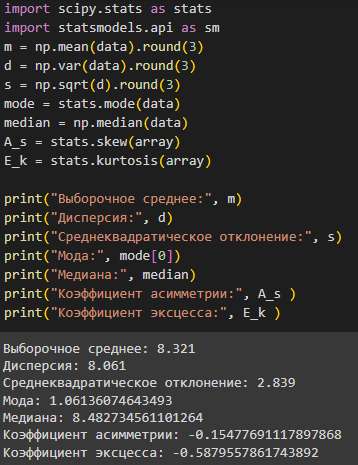
Рисунок 9 – Определение метрик

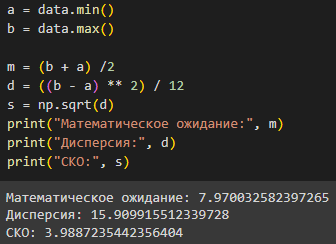
Рисунок 10 – Определение мат. ожидания, дисперсии и СКО

Гистограмма напоминает треугольное распределение, был дополнительно построен график квантиль-квантиль для выборки (Рисунок 11).

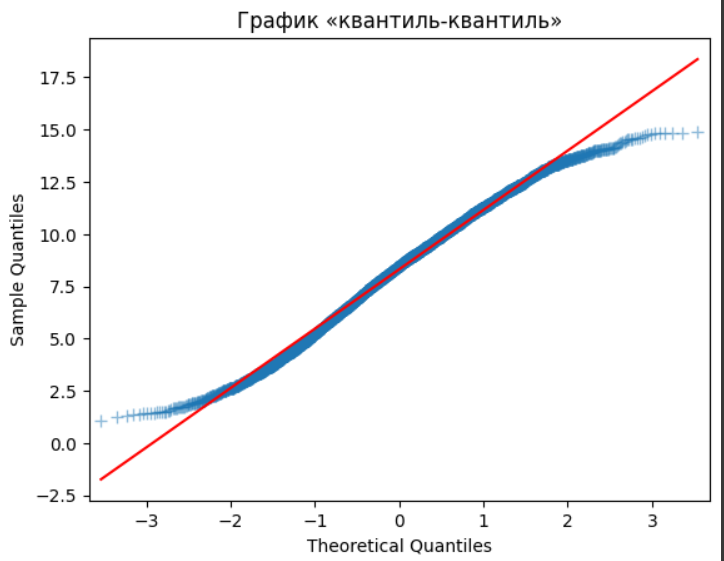
Рисунок 11 – квантиль-квантиль для выборки по варианту

С помощью библиотеки numpy была сгенерирована выборка треугольного распределения и построены графики (Рисунок 12 - 14).

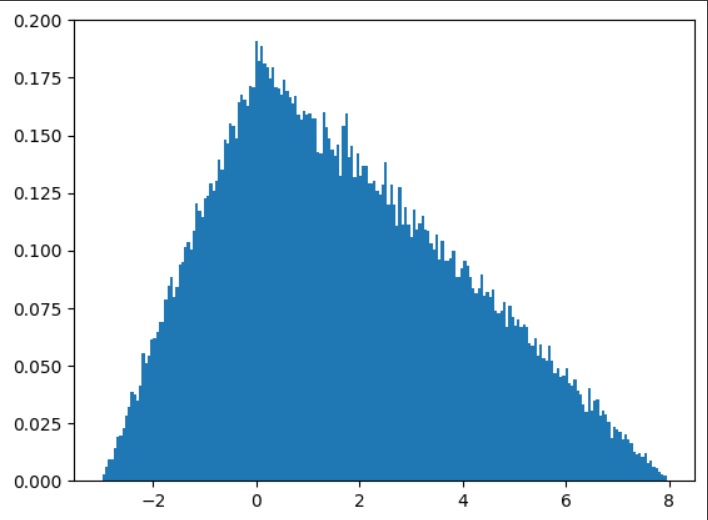
Рисунок 12 – Гистограмма для треугольного распределения

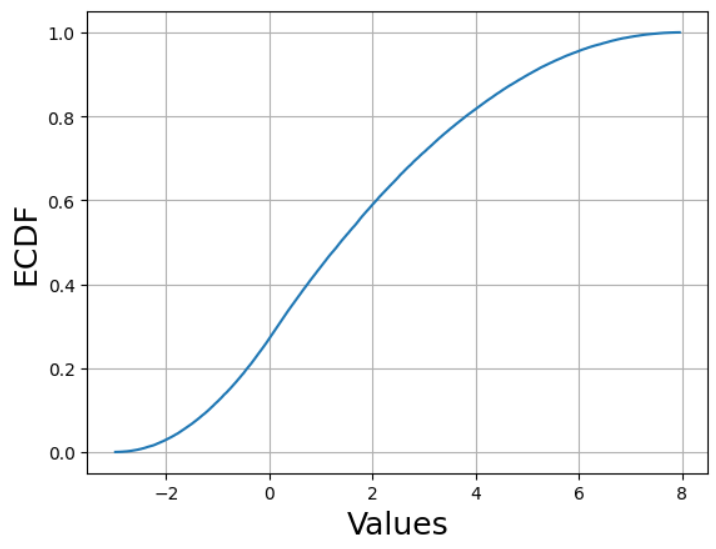
Рисунок 13 – Эмпирическая функция для треугольного распределения

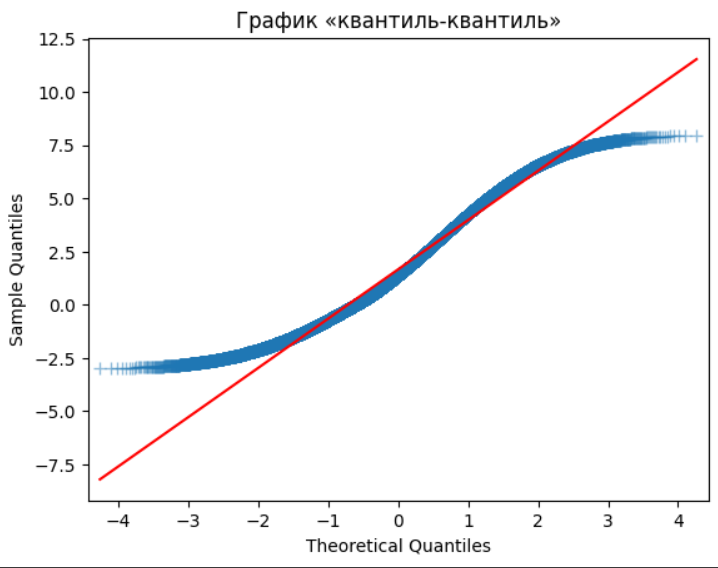
Рисунок 14 – Квантиль-квантиль для треугольного распределения

Графики гистограмм и квантиль-квантиль выборки по варианту и выборки треугольного распределения похожи, можно сделать вывод, что исследуемая выборка имеет треугольное распределение.

3 Вывод

В ходе выполнения лабораторной работы была проведена обработка двух выборок данных, построены графики полигона частот, эмпирической функции распределения, гистограммы, вычислены метрики. В ходе анализа сделаны выводы, что первая выборка имеет нормальное распределение. Для определения типа распределения второй выборки была сгенерирована выборка треугольного распределения, проведено сравнение графиков, которое показало высокую схожесть выборки из второй части задания и треугольного распределения.