
М2
.docxГУАП
КАФЕДРА № 41
ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
старший преподаватель Е.К. Григорьев
должность, уч. степень, звание подпись, дата инициалы, фамилия
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ № 2
МОДЕЛИРОВАНИЕ ГЕНЕРАТОРОВ НОРМАЛЬНО РАСПРЕДЕЛЕННЫХ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ
по курсу: МОДЕЛИРОВАНИЕ
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № подпись, дата инициалы, фамилия
Санкт-Петербург 2024
1 Цель работы
Получить навыки моделирования нормально распределенных псевдослучайных чисел в программной среде MATLAB/GNU Octave, а также первичной оценки качества полученных псевдослучайных чисел.
2 Ход работы
Вариант 15
m
= 6,
 =
1.
=
1.
Вычислена плотность вероятности по формуле:
 ,
,
 ,
,




Построен график (Рисунок 1).
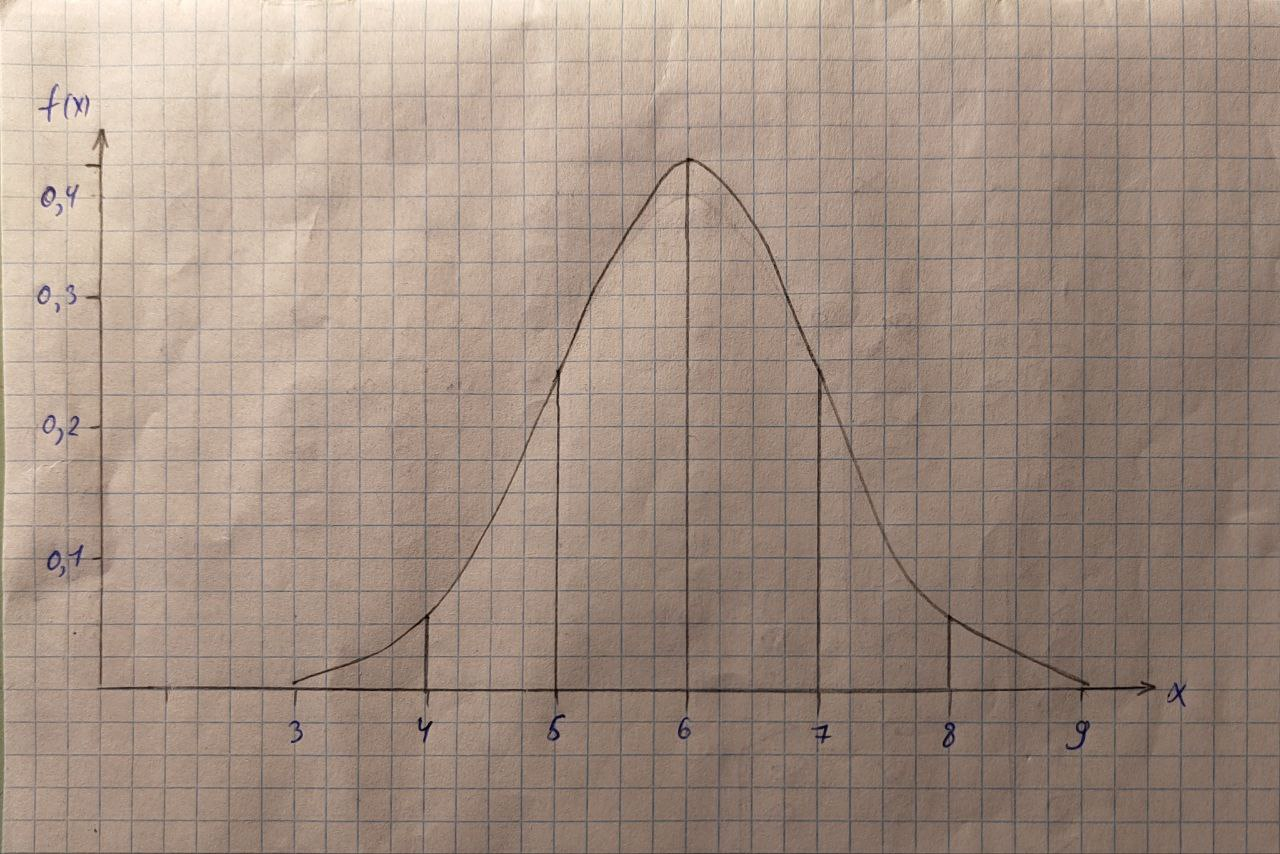
Рисунок 1 – График плотности распределения
Для получения функции распределения необходимо интегрировать функцию плотности вероятности распределения:
 =
= ,
,
Интеграл такого рода не выражается. Для его нахождения используется функция Лапласа:

 ,
тогда:
,
тогда:
 ,
,
С помощью таблицы значений функции Лапласа и свойства рассчитаны значения функции распределения:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Построен график (Рисунок 2).

Рисунок 2 – График функции распределения
Также графики были построены с помощью языка программирования Python (Рисунок 3). Код представлен в листинге 1.

Рисунок 3 – Графики
Листинг 1 – Код для построения графиков
import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
m = 6
sigma = 1
def distribution_density(x, m, sigma):
coefficient = 1 / np.sqrt(2 * np.pi * sigma)
exponent = np.exp(-((x - m) ** 2) / (2 * sigma**2))
return coefficient * exponent
def standard_normal_distribution(t):
return np.exp(-t**2 / 2)
def laplace_integral(x):
result, _ = integrate.quad(standard_normal_distribution, -np.inf, x)
return (1 / np.sqrt(2 * np.pi)) * result
def distribution_func(x, m, sigma):
return 0.5 + 0.5* laplace_integral((x - m) / sigma)
x_values = np.linspace(m - 3 * np.sqrt(sigma), m + 3 * np.sqrt(sigma))
distribution_values = distribution_density(x_values, m, sigma)
plt.figure(figsize = (20, 8))
plt.subplot(121)
plt.plot(x_values, distribution_values)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('График плотности распределения')
plt.grid(True)
X_values = np.linspace(m - 3 * sigma, m + 3 * sigma, 1000)
F_X_values = [distribution_func(x, m, sigma) for x in X_values]
plt.subplot(122)
plt.plot(X_values, F_X_values, color='green')
plt.title('График функции распределения')
plt.xlabel('x')
plt.ylabel('F(x)')
plt.grid(True)
plt.show()
Разработан алгоритм генерации псевдослучайных чисел, основанный на центральной предельное теореме (Листинг 2). Данный способ основан на том, что сумма n одинаково распределенных независимых случайных величин X со средним Mx и дисперсией Dx стремится к нормально распределенной величина с параметрами nMx, nDx, при бесконечном увеличении n. Формула представлена на рисунке 4.

Рисунок 4 – Формула для генерации, основанной основанного на центральной предельной теореме
Листинг 2 – Функция алгоритма, основанного на центральной предельной теореме
def uniform_to_normal(n, m, sigma):
# Генерация равномерно распределенных чисел
uniform_random_values = np.random.uniform(low=0.0, high=1.0, size=(n, 12))
# Преобразование выборки равномерно распределенных чисел в выборку нормально распределенных
normal_random_values = m + sigma * (np.sum(uniform_random_values, axis = 1) - 6)
return normal_random_values
Разработан алгоритм генерации псевдослучайных чисел, основанный на преобразовании Бокса-Мюллера (Листинг 3). Этот метод позволяет генерировать сразу две независимые псевдослучайные величины со стандартным нормальным распределением. Формулы представлены на рисунке 5.

Рисунок 5 – Формулы преобразования Бокса-Мюллера
Листинг 3 – Функция преобразования Бокса-Мюллера
def box_muller_transformation(n, m, sigma):
normal_random_numbers = []
for _ in range(n // 2):
# Генерация двух равномерно распределенных случайных величин
r1, r2 = np.random.uniform(low=0.0, high=1.0, size=2)
# Выполнение преобразования
z0 = np.cos(2 * np.pi * r1) * np.sqrt(-2 * np.log(r2))
z1 = np.sin(2 * np.pi * r1) * np.sqrt(-2 * np.log(r2))
normal_random_numbers.extend([m + sigma * z0, m + sigma * z1])
return np.array(normal_random_numbers)
Разработан алгоритм генерации псевдослучайных чисел, полярном методе Марсальи (Листинг 4). Метод представляет собой оптимизированную версию преобразования Бокса-Мюллера, где нет необходимости вычислять функции cos() и sin(). Формулы представлены на рисунке 6.

Рисунок 6 – Формулы полярного метода Марсальи
Листинг 4 – Функция полярного метода Марсальи
def marsaglia_polar_method(n, m, sigma):
normal_random_numbers = []
for _ in range(n):
# Генерация пары равномерно распределенных чисел
x, y = np.random.uniform(-1, 1, size=2)
s = x**2 + y**2
# Отбрасывание s, не попадающих в [0; 1]
while s >= 1 or s == 0:
x, y = np.random.uniform(-1, 1, size=2)
s = x**2 + y**2
z0 = np.sqrt(-2 * np.log(s) / s) * x
z1 = np.sqrt(-2 * np.log(s) / s) * y
normal_random_numbers.extend([m + sigma * z0, m + sigma * z1])
return np.array(normal_random_numbers)
Разработан алгоритм генерации псевдослучайных чисел, с помощью встроенной функции генерации (Листинг 5).
Листинг 5 – Генерация с помощью встроенной функции
def numpy_random(n, m, sigma):
standard_normal_random_numbers = np.random.randn(n)
normal_random_numbers = m + sigma * standard_normal_random_numbers
return normal_random_numbers
Для каждого алгоритма генерации сгенерированы выборки по 1000, 5000 и 10000 чисел. Для каждого набора случайных чисел построены графики: гистограмма, график эмпирической функции, распределение на плоскости, «квантиль-квантиль» (Рисунок 7 - 10).

Рисунок 7 – Гистограммы
Гистограммы показали нормальное распределение для всех выборок. С увеличением размера выборки гистограмма становится плавнее.

Рисунок 8 – Графики эмпирической функции
Все выборки показали характерный для нормального распределения график эмпирической функции.
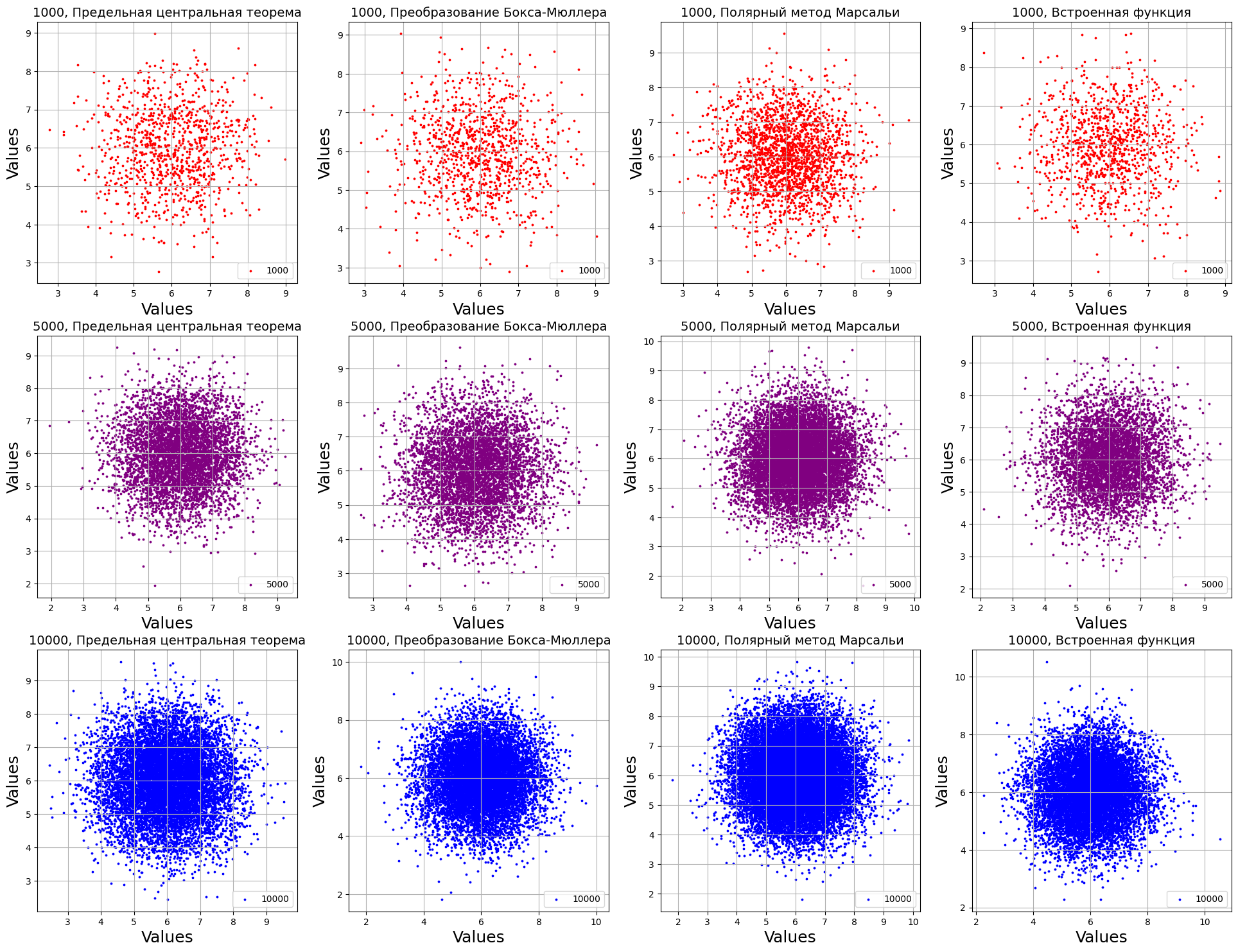
Рисунок 9 – Распределение на плоскости
Тест распределение на плоскости показал свойственные для нормального распределения результаты. Точки сгруппированы в центре графика, что говорит, о высокой плотности значений вокруг среднего.

Рисунок 10 – Графики «квантиль-квантиль»
Получившиеся графики соответствуют нормальному распределению, большинство точек располагается на прямой линии.
Для каждого набора случайных чисел вычислены метрики (Рисунок 11).

Рисунок 11 – Метрики
Метрики всех выборок показали значения, близкие к аналитическим, генераторы работают стабильно и дают значения, соответствующие нормальному распределению.
Код для построения графиков и вычисления метрик представлен в листинге 6.
Листинг 6 – Построение графиков и вычисление метрик
def randomizer(generator, n):
if generator == 'Предельная центральная теорема':
result = uniform_to_normal(n, m, sigma)
elif generator == 'Преобразование Бокса-Мюллера':
result = box_muller_transformation(n, m, sigma)
elif generator == 'Полярный метод Марсальи':
result = marsaglia_polar_method(n, m, sigma)
elif generator == 'Встроенная функция':
result = numpy_random(n, m, sigma)
return result
amounts = [1000, 5000, 10000]
colors = ['red', 'purple', 'blue']
generators = ['Предельная центральная теорема', 'Преобразование Бокса-Мюллера', 'Полярный метод Марсальи', 'Встроенная функция']
records = []
for i, amount in enumerate(amounts):
for j, generator in enumerate(generators):
random = randomizer(generator, amount)
x = np.linspace(min(random), max(random), amount)
ecdf = ECDF(random)
y = ecdf(x)
# Гистограмма
plt.figure(1, figsize=(24, 18))
plt.subplot(3, 4, i * 4 + j + 1)
plt.hist(random, bins=50, color=colors[i], alpha = 0.7)
plt.title(f'{amount}, {generator}', fontsize = 14)
plt.xlabel('Value', fontsize = 16)
plt.ylabel('Frequency', fontsize = 16)
plt.grid(True)
# График ECDF
plt.figure(2, figsize=(24, 18))
plt.subplot(3, 4, i * 4 + j + 1)
plt.plot(x, y, colors[i])
plt.title(f'{amount}, {generator}', fontsize=14)
plt.xlabel('Values', fontsize=18)
plt.ylabel('ECDF', fontsize=18)
plt.legend([str(amount)], fontsize=14, loc='lower right')
plt.grid(True)
random_shifted = np.roll(random, -1)
# Диаграмма рассеивания
plt.figure(3, figsize=(24, 18))
plt.subplot(3, 4, i * 4 + j + 1)
plt.scatter(random, random_shifted, s=3, c=colors[i], label=f'{amount}')
plt.title(f'{amount}, {generator}', fontsize=14)
plt.xlabel('Values', fontsize=18)
plt.ylabel('Values', fontsize=18)
plt.legend(loc='lower right')
plt.grid(True)
mean_val = round(np.mean(random), 3)
var_val = round(np.var(random), 3)
std_val = round(np.std(random), 3)
record = {
'Количество': amount,
'Генератор': generator,
'Мат. ожидание': mean_val,
'Дисперсия': var_val,
'Среднекв. откл.':std_val
}
records.append(record)
fig, axes = plt.subplots(len(amounts), len(generators), figsize=(24, 18))
for i, amount in enumerate(amounts):
for j, generator in enumerate(generators):
random = randomizer(generator, amount)
x = np.linspace(min(random), max(random), amount)
sm.qqplot(random, ax=axes[i, j], line='s', label=f'{amount}, {generator}', alpha=0.5)
axes[i, j].set_title(f'{amount}, {generator}', fontsize=12)
axes[i, j].set_xlabel('Теоретические квантили', fontsize=12)
axes[i, j].set_ylabel('Квантили исследуемой выборки', fontsize=12)
axes[i, j].grid(True)
# Вычисление метрик аналитически
mean_analytical = m
variance_analytical = sigma**2
std_analytical = sigma
records.append({
'Количество': "Аналитически",
'Генератор': "Нормальное распределение",
'Мат. ожидание': mean_analytical,
'Дисперсия': variance_analytical,
'Среднекв. откл.':std_analytical
})
plt.show()
df = pd.DataFrame(records)
display(df)
3 Вывод
В ходе выполнения лабораторной работы построены графики плотности распределения и функции распределения для нормального распределения. С помощью программных средств реализованы генераторы нормально распределенных псевдослучайных чисел, основанные на центральной предельной теореме, преобразовании Бокса-Мюллера, полярном методе Марсальи и встроенной функции генерации. Сгенерированы выборки по 1000, 5000 и 10000 чисел, построены графики, вычислены метрики. Все генераторы показали значения метрик, близкие к аналитическим, генераторы работают стабильно.
