ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				В.В. Боженко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

КЛАСТЕРИЗАЦИЯ

по курсу: ВВЕДЕНИЕ В АНАЛИЗ ДАННЫХ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

Цели работы: изучение алгоритмов и методов кластеризации на практике.

Ход работы

Вариант 5

Использована функция для создания набора данных. n - число объектов в каждой группе (всего 3 группы), seed - зерно, необходимое для воспроизводимости случайных значений. (Рисунок 1).

Рисунок 1 – Функция

Созданы и выведены на экран наборы данных train и test (Рисунок 2, 3).

Рисунок 2 – Набор данных train

Рисунок 3 – Набор данных test

Выполнена стандартизация данных с помощью StandardScaler (Рисунок 4).

Рисунок 4 – Стандартизация

Выполнена кластеризация данных методом KMeans для трех кластеров. (Рисунок 5, 6).

Рисунок 5 – Кластеризация train

Рисунок 6 – Кластеризация test

Проведена визуализация кластеров, объекты из разных кластеров имеют разные цвета. Центры кластеров отображены красным цветом (Рисунок 7 - 9).

Рисунок 7 – Создание графиков

Рисунок 8 – Кластеризация train

Рисунок 9 – Кластеризация test

По графикам можно сказать, что в test наблюдается больший разброс значений в кластерах, центры кластеров незначительно смещены относительно центров кластеров train.

Посчитан коэффициент силуэта (Рисунок 10)

Рисунок 10 – Коэффициент силуэта

Высокое значение коэффициента силуэта (0.7 и 0.67) свидетельствует о том, что кластерная структура хорошо выражена, и количество кластеров соответствует естественной группировке данных.

Также были построены графики для кластеризации n_clusters = 2 и n_clusters = 4 (Рисунок 11, 12).

Рисунок 11 – Кластеризация 2

В кластерах наблюдаются большие выбросы, в тренировочной выборке наблюдается смещение центра кластера, в обеих выборках наблюдается крупный кластер, в котором объекты кластера находятся слишком далеко от центра. Число кластеров 2 не подходит для данной модели.

Рисунок 12 – Кластеризация 4

Наблюдаются соприкасающиеся кластеры, значительные выбросы. В тренировочной выборке центры кластеров сильно смещены относительно их объектов. Число кластеров 4 не подходит.

Построен график по методу локтя (Рисунок 13).

Рисунок 13 – График по методу локтя

Построенный график подтверждает, что оптимальное число кластеров равняется 3.

Импортирован датасет с информацией о клиентах фитнес-клуба (Рисунок 14).

Рисунок 14 – Импорт датасета

Проведена предварительная обработка данных (Рисунок 15 - 18).

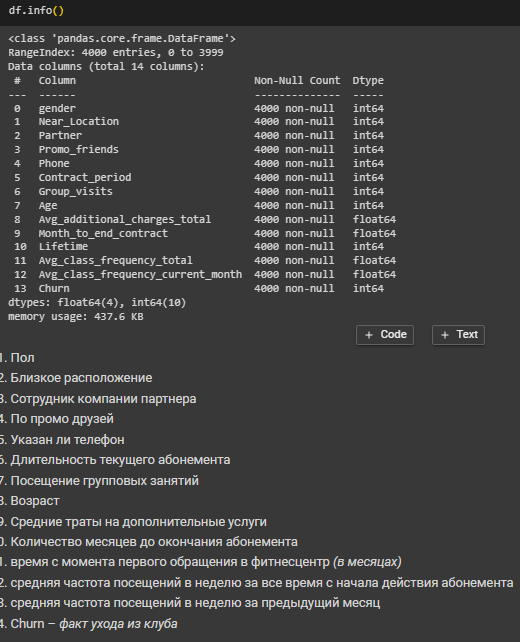
Рисунок 15 – Информация о столбцах датасета

Рисунок 16 – Число пустых ячеек

Рисунок 17 – Число дубликатов

Рисунок 18 – Уникальные значения

Несоответствий типов данных, явных и неявных дубликатов не обнаружено.

Выбрана целевая переменная Churn, построена матрица диаграмм рассеяния (Рисунок 19).

Рисунок 19 – Матрица диаграмм рассеяния

Большинство клиентов в этом наборе данных не покинули фитнес-клуб. Большая часть клиентов, у которых осталось меньше 5 месяцев до окончания контракта, покинули фитнес-клуб. Клиенты, покинувшие клуб, наиболее вероятно провели в нём меньше 3 месяцев.

Данные были стандартизированы (Рисунок 20).

Рисунок 20 – Стандартизация данных

С помощью KElbowVisualizer было найдено оптимальное число кластеров - 4 (Рисунок 21).

Рисунок 21 – Метод локтя

Выполнена кластеризация и отображено количество объектов каждого кластера (Рисунок 22).

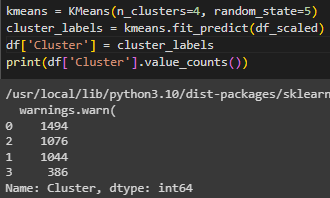
Рисунок 22 – Количество объектов каждого кластера

Подсчитаны и выведены медианные значения для каждого столбца по кластерам (Рисунок 23).

Рисунок 23 – Медианные значения

0 кластер - наименьшая длительность контракта, наименьшее время с первого обращения. Вероятно, кластер содержит записи о новых клиентах

1 кластер - небольшая длительность контракта, наибольшее число посещений.

2 кластер - большинстов клиентов живут близко к клубу, большинство пришло по приглашению друзей, наибольшая длительность контракта, наибольшее время до окончания контракта. Вероятно, кластер содержит записи о постоянных клиентах, живущих близко к клубу.

3 кластер - много клиентов живут близко к клубу, телефон не указан, средняя длительность контракта, среднее число посещений

Возраст клиентов всех кластеров примерно равен 30

Посчитаны метрики (Рисунок 24).

Рисунок 24 – Метрики

Выведены объекты каждого кластера (Рисунок 24 - 27).

Рисунок 24 – Объекты кластера 0

Рисунок 25 – Объекты кластера 1

Рисунок 26 – Объекты кластера 2

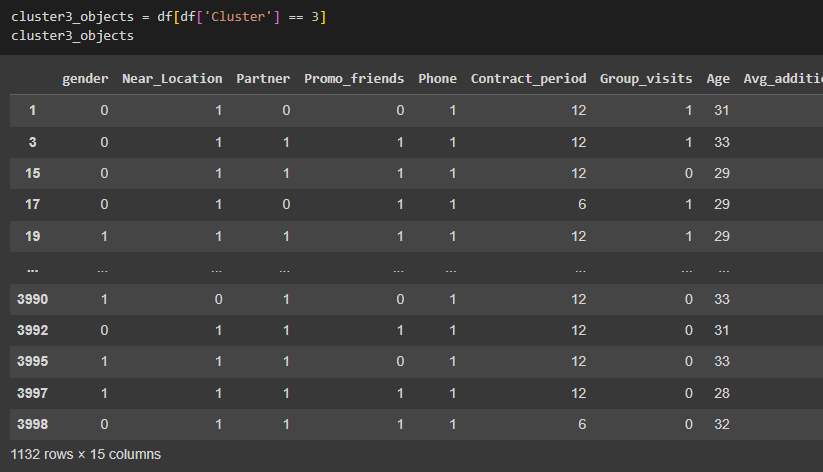
Рисунок 27 – Объекты кластера 3

Выполнена кластеризация иерархическим агломеративным методом. Для этого построена дендрограмма (Рисунок 28).

Рисунок 28 – Дендограмма

Иерархическая кластеризация представляет собой процесс иерархического построения дерева кластеров с использованием различных методов объединения или разделения кластеров. В результате получается дерево (дендрограмма), которое позволяет анализировать иерархическую структуру данных и определять кластеры на разных уровнях иерархии.

Дополнительное задание №7

Выполнить нормализацию данных с помощью MinMaxScaler, MaxAbsScaler и сравнить полученные итоговые метрики с теми, что были получены на данных, нормализованных с помощью StandardScaler.

StandardScaler производит масштабирование данных, центрируя их вокруг среднего значения и шкалируя по стандартному отклонению.

MinMaxScaler преобразует данные в интервал между указанными минимальным и максимальным значениями (обычно 0 и 1). Проведена нормализация, разделение на кластеры, вычислены метрики (Рисунок 29, 30).

Рисунок 29 – Нормализация MinMaxScaler

Рисунок 30 – Разделение на кластеры и вычисление метрик

MaxAbsScaler масштабирует данные по максимальному абсолютному значению. Проведена нормализация, разделение на кластеры, вычислены метрики (Рисунок 31, 32).

Рисунок 31 – Нормализация MaxAbsScaler

Рисунок 32 – Разделение на кластеры и вычисление метрик

Метрики, полученные в результате нормализации данных тремя разными методами, были отображены в одной таблице (Рисунок 33).

Рисунок 33 – Таблица с метриками

Судя по метрикам, можно сказать, что нормализация данных с помощью StandardScaler привела к наилучшим результатам, индекс FMI 0.48 говорит о среднем сходстве между кластерами, низкое значение коэффициента силуэта, близкое к нулю, говорит о близком расположении объектов внутри кластеров и нечетком разделении между кластерами.

Число объектов в каждом кластере для всех трех методов нормализации было отображено в одной таблице (Рисунок 34).

Рисунок 34 – Таблица с числом объектов в каждом кластере

При разделении на кластеры данных, нормализованных с помощью MaxAvgScaler наблюдается незначительная разница (103) в количестве объектов между самым крупным и самым малым кластерами, в то время как в MinMaxScaler она больше (489), а в StandardScaler она составила 1108, что говорит о неравномерном распределении объектов между кластерами.

Ссылка на Google Colab:

Вывод:

В ходе выполнения лабораторной работы была произведена кластеризация двумя способами: методом K-Means и иерархическим агломеративным методом. Для нахождения оптимального числа кластеров использовался метод локтя. При неверно подобранном числе кластеров, кластеры могут соприкасаться, пересекаться, объекты в них могут находиться далеко друг от друга, что негативно влияет на группировку объектов.

Метод k-средних требует заранее определить число кластеров, от чего зависит качество кластеризации. При неправильно подобранном количестве кластеров, кластеризация будет неэффективной.

В результате иерархической агломеративной кластеризации создается иерархия (дерево) вложенных кластеров, оно более наглядно позволяет увидеть оптимальное число кластеров, а также их структуру.