Боженко ЛР / анализ данных3 исправленный

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

старший преподаватель				В.В. Боженко
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

РЕГРЕССИОННЫЙ АНАЛИЗ

по курсу: ВВЕДЕНИЕ В АНАЛИЗ ДАННЫХ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2023

Цели работы: изучение алгоритмов и методов регрессии на практике.

Ход работы

Вариант 15

Импортируются все необходимые библиотеки (Рисунок 1).

Рисунок 1 – Импорт библиотек

Задаются значения переменных соответственно варианту, выполняется обучение модели (Рисунок 2, 3).

Рисунок 2 – Задание значений

Рисунок 3 - Обучение модели

Выполняется предсказание при помощи метода predict. Создан и выведен на экран датафрейм с истинными и предсказанными значениями (Рисунок 4).

Рисунок 4 – Предсказанные и истинные значения

Для лучшего понимания качества предсказания среднеквадратичная ошибка, средняя абсолютная ошибка, корень из среднеквадратичной ошибки, коэффициент детерминации (Рисунок 5).

Рисунок 5 – Подсчет метрик

Высокий коэффициент детерминации (0.84) говорит о довольно хорошем качестве предсказаний.

Посчитаны и выведены значения коэффициентов a (коэффициент наклона) и b (коэффициент смещения) (Рисунок 6).

Рисунок 6 – Коэффициенты

Выполнена визуализация регрессии (Рисунок 7).

Рисунок 7 – Визуализация регрессии

Построен график с разницей предсказанного и истинного значения по каждой точке. Если точка находится выше линии нулевой разницы, то предсказанное значение больше истинного, если ниже - предсказанное меньше истинного (Рисунок 8).

Рисунок 8 – График разницы

Согласно заданию, построен график с истинными и предсказанными значениями (Рисунок 9).

Рисунок 9 – График по заданию

Создан массив x2, массивы x1 и x2 объединены в двумерный массив x_array, осуществлен вывод x_array (Рисунок 10).

Рисунок 10 – Создание и вывод массива

Выполнена инициализация модели линейной регрессии, эта модель обучена на заданной выборке (Рисунок 11).

Рисунок 11 – Инициализация и создание линейной регрессии

Выполнено предсказание y2 по данным модели, создан и выведен на экран датафрейм с истинными и предсказанными значениями (Рисунок 12).

Рисунок 12 – Предсказание

Подсчитаны метрики качества регрессии (MSE, MAE, RMSE, R2) (Рисунок 13).

Рисунок 13 – подсчет метрик

Высокий коэффициент детерминации (0.84) говорит о довольно хорошем качестве предсказаний.

Посчитаны и выведены значения коэффициентов a (коэффициент наклона) и b (коэффициент смещения) (Рисунок 14).

Рисунок 14 – Подсчет коэффициентов

Построен график с разницей предсказанного и истинного значения по каждой точке. Если точка находится выше линии нулевой разницы, то предсказанное значение больше истинного, если ниже - предсказанное меньше истинного (Рисунок 15).

Рисунок 15 – График разницы

По графику видно, что число предсказанных значений превышающих истинные больше.

Построена таблица с метриками простой линейной регресиии и множественной линейной регрессии (Рисунок 16).

Рисунок 16 – Таблица с метриками

Модель, обученная парной линейной регрессии, показала очень схожие результаты с моделью, обученной простой линейной регресссии, метрики оказались практически равны.

Для реализации модели полиномиальной регрессии импортирована PolynomialFeatures. poly_features содержит полиномиальные признаки 2 степени. Метод fit_transform принимает значения и преобразует их с учетом полиноминальных признаков. model 3 - объект модели линейной регрессии (Рисунок 17).

Рисунок 17 – Создание полиноминальной регрессии

Выполнено предсказание и выведено на экран (Рисунок 18).

Рисунок 18 – Выполнение предсказания

Подсчитаны метрики и реализован график по данным (Рисунок 19).

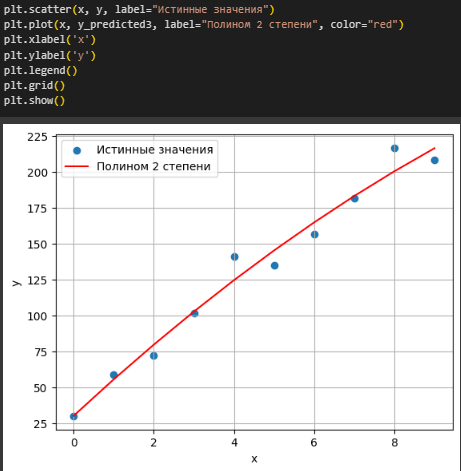
Рисунок 19 – Подсчет и график

По графику видно, что использование полиноминальной регрессии приводит к лучшим результатам из-за использования нелинейного уравнения, что позволяет модели более точно выполнять предсказания.

Аналогично эти же действия выполнены для полиномов 4 и 10 степеней (Рисунок 20 - 22).

Рисунок 20 – Полином 4 степени

Рисунок 21 – Полином 10 степени

Рисунок 22 – Общий график

Создана таблица с метриками для предсказаний с каждой степенью полинома (Рисунок 23).

Рисунок 23 – Таблица с метриками

Судя по метрикам, все 3 модели показали высокую степень достоверности предсказаний (от 0.97), но при достижении определенной степени полинома, модель переобучается.

Исходя из результатов обучения моделей с разными степенями полинома, можно сказать, что с ростом степени полинома предсказанные значения становятся ближе к истинным и даже становятся равными им. Выбор высокой степени полинома, при которой предсказанные значения слишком близки к реальным, грозит переобучением, что отразится на способности модели обобщаться на новые данные.

Импортирован набор данных car_price, содержащий данные об автомобилях (Рисунок 24).

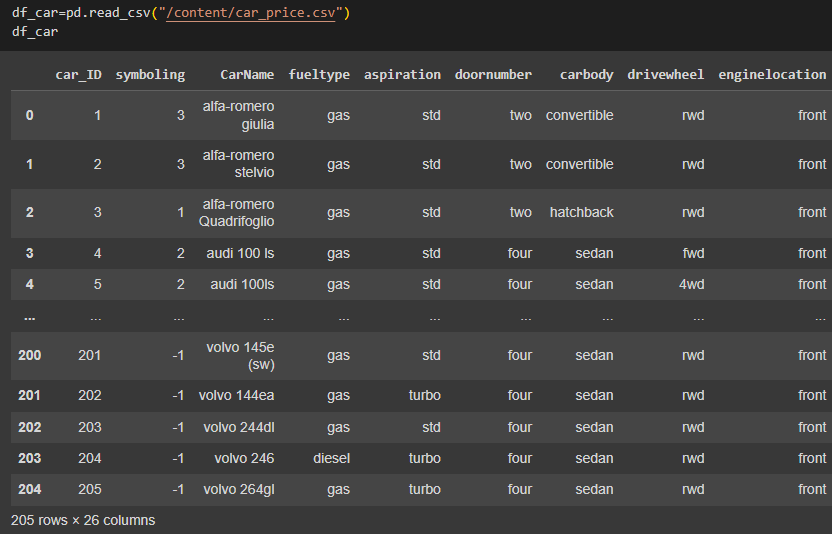
Рисунок 24 – Импорт датасета

Выбрана переменная price (цена автомобиля), построена гистограмма для этого столбца (Рисунок 25).

Рисунок 25 - Гистограмма

По гистограмме видно, что наибольшее число автомобилей имеют цену от 5000 до 10000, наименьшее - от 28000 до 29000 и от 40000 до 46000

Построен boxplot (Ящик с усами) (Рисунок 26).

Рисунок 26 – Ящик с усами

Boxplot или "ящик с усами" состоит из квартилей. Нижний квартиль расположен так, что 25% значений выборки меньше его, 75% больше. Второй квартиль - 50% меньше и 50% больше. Третий квартиль - 75% меньше и 25% больше. Четвертый - значения справа являются выбросами, нетипичными значениями. Наблюдаются многочисленные выбросы.

Построена матрица диаграмм рассеяния (Рисунок 27).

Рисунок 27 – Матрица диаграмм рассеяния

По матрице видно, что у седанов наибольшее число пиковых оборотов, вес автомобиля и размер двигателя, максимальный объем двигателя чаще всего у хэтчбеков.

Данные разделены на обучающую и тестовую выборки (Рисунок 28).

Рисунок 28 – Разделение данных на выборки

Отобраны и нормализованы числовые столбцы (Рисунок 29).

Рисунок 29 – Нормализация

Инициализирован объект линейной регрессии, проведено обучение (Рисунок 30).

Рисунок 30 – Инициализация и обучение объекта модельной регрессии

Осуществлён подбор оптимальных параметров с помощью GridSearchCV (Рисунок 31).

Рисунок 31 – Подбор оптимальных параметров

Выполнено предсказание по оптимальной модели (Рисунок 32).

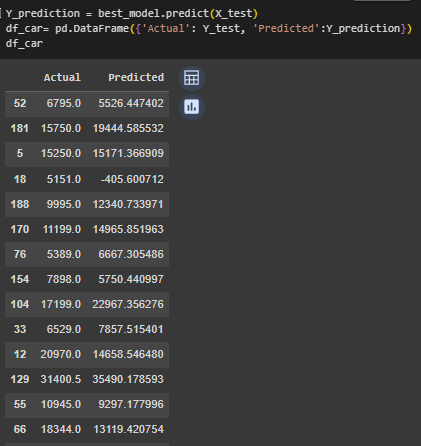
Рисунок 32 – Предсказание

Вычислены метрики (Рисунок 33).

Рисунок 33 – Метрики

Вычислены коэффициенты влияния для признаков автомобилей, чем больше значение коэффициента, тем сильнее связь между признаком и целевой переменной (Рисунок 34).

Рисунок 34 – Коэффициенты

Для более наглядного отображения влияния коэффициентов была построена гистограмма (Рисунок 35).

Рисунок 35 – Гистограмма влияния признаков

Наиболее сильно влияющими на целевую переменную оказались признаки boreratio, carwidth и symboling.

Разработан график с предсказанными и истинными значениями (Рисунок 36)

Рисунок 36 – График истинных и предсказанных значений

Выполнена регрессия методом k-ближайших соседей (Рисунок 37).

Рисунок 37 - Регрессия методом k-ближайших соседей

Выполнена регрессия деревом решений (Рисунок 38).

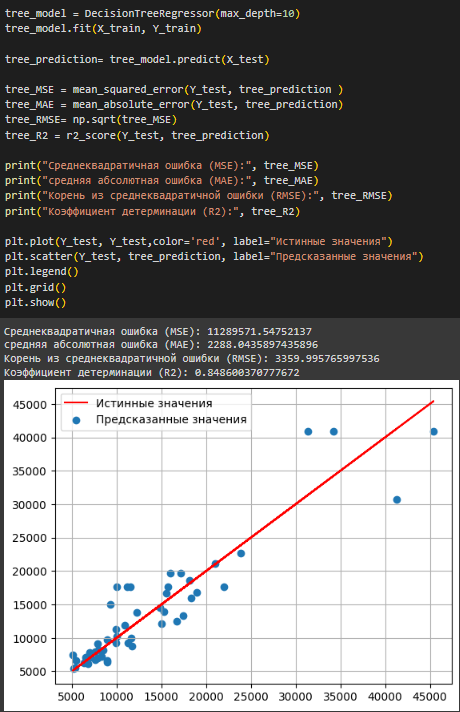
Рисунок 38 – Регрессия деревом решений

Все реализованные модели регрессии были отображены на одном графике (Рисунок 39).

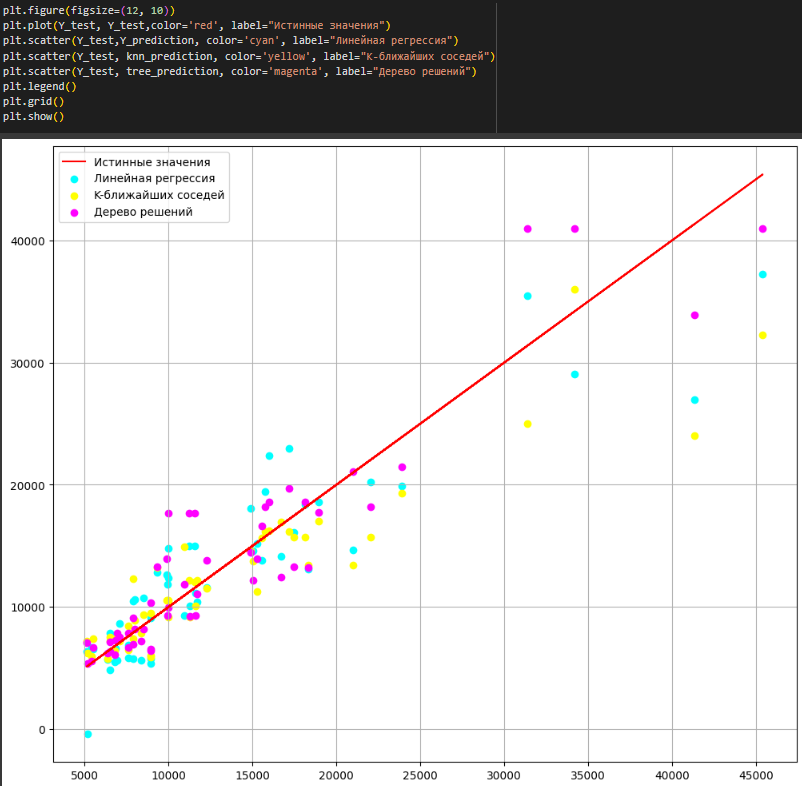
Рисунок 39 – Общий график

Исходя из полученных метрик и графика, можно сказать, что для анализируемого набора данных больше всего подходит модель дерева решений, т.к. она показала наиболее близкие к истинным предсказания, имеет наибольший коэффициент детерминации (0.86)

Дополнительное задание №5

Выполнить L2-регуляризацию (Ridge). Сравнить результаты, полученные другими методами. Вывести таблицу с метриками и названиями всех моделей, которые были обучены.

Инициализирован объект L2-регуляризации, обучена модель, выполнено предсказание (Рисунок 40).

Рисунок 40 – Предсказание

Посчитаны метрики (Рисунок 41).

Рисунок 41 - Метрики

Создана таблица с метриками каждой использованной на наборе данных модели (Рисунок 42).

Рисунок 42 – Таблица метрик

Наиболее эффективной является модель дерева решений, на втором месте - L2-регуляризация, на третьем - линейная регрессия, на четвертом - метод k-ближайших соседей.

Ссылка на Google Colab:

Вывод: В ходе выполнения лабораторной работы была реализована простая линейная регрессия и парная линейная регрессия. Результаты предсказаний этих двух моделей оказались практически идентичными, значения метрик почти равны.

При работе с моделью полиноминальной регрессии, было замечено, что с возрастанием степени полинома, предсказания становятся ближе к истинным значениям, пока не станут им равны. Слишком большая степень полинома приводит к переобучению.

Был рассмотрен набор данных с информацией об автомобилях, целевой выбрана переменная price (цена), наибольшее влияние на неё оказали признаки boreratio, symboling и carwidth. Для этого набора данных наиболее эффективной оказалась модель дерева решений.