
Расчетно графическая работа
.pdfМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
доц., канд. физ.-тех наук, доц. |
|
|
|
Г.Н. Дьякова |
|
|
|
|
|
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
СТАТИСТИЧЕСКАЯ ОБРАБОТКА ВЫБОРКИ
по дисциплине: МАТЕМАТИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
РАБОТУ ВЫПОЛНИЛ |
|
|
|
|
|
|
СТУДЕНТ ГР. № |
4116 |
|
|
|
В.С. Пахомов |
|
|
|
|
|
|
|
|
|
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2022
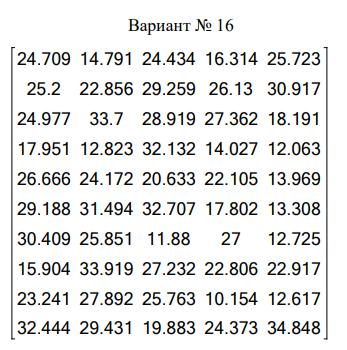
Заданную выборку объемом n=50:
1.Сгруппировать в виде вариационного ряда (сосчитать размах выборки и разбить на 10 одинаковых интервалов).
2.Построить гистограмму и полигон относительных частот.
3.Вычислить выборочное среднее, оценку второго центрального момента,
несмещенную оценку для дисперсии.
4.Считая, что изучаемый параметр у элементов генеральной совокупности распределен нормально, найти доверительный интервал для математического ожидания с доверительной вероятностью 0.90, при условиях известной/неизвестной дисперсии.
5.Считая, что изучаемый параметр у элементов генеральной совокупности распределен нормально, найти доверительный интервал для дисперсии с доверительной вероятностью 0.90.
6.Используя критерии Пирсона при уровне значимости 0.10, проверить,
согласуется ли гипотеза о нормальном распределении генеральной совокупности
с эмпирическим распределением выборки и проанализировать полученный
результаты.
Вариант №16
1.
Размах выборки вычисляется по формуле: ∆ = xmax - xmin =34.848 - 2.851= 31.997
Преобразуем вариационный ряд в интервальный с числом интервалов N = 10,
длиной интервала - h.
= |
∆ |
= |
31.997 |
≈ 3.1 |
||
|
|
|
|
|||
N |
10 |
|
||||
Интервальный ряд:
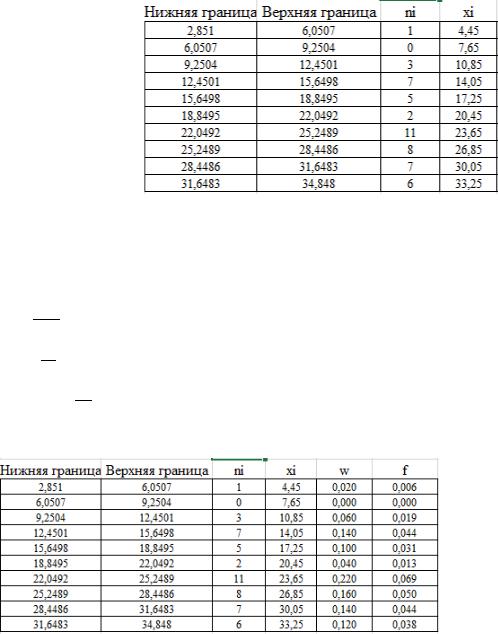
2.
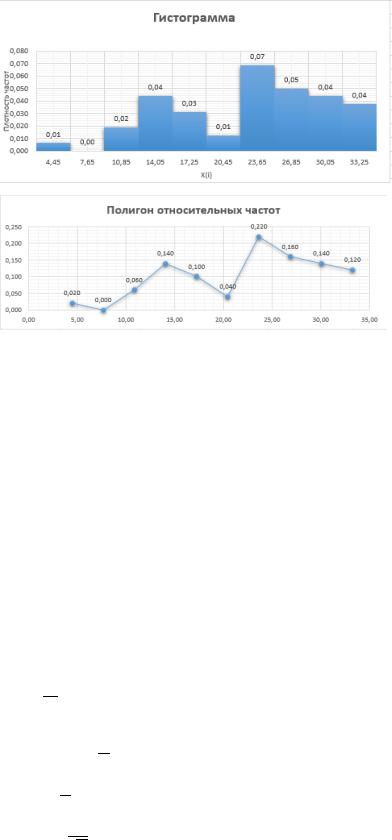
Построим гистограмму и полигон относительных частот c помощью программы Excel.
xi = +2 - середина каждого интервала;
wi = , где n = 50 (по условию задачи) - относительную частота;
( ) = - плотность частот.
Все вычисленные параметры занесем в таблицу:
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выборочное среднее: ̅ = |
1 |
∑ |
|
|
= 22,95 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка второго центрального момента: |
|
|
= |
1 |
∑ |
|
|
( |
̅̅̅2 |
= 52,54 |
||||||||||
2 |
|
|
=1 |
− ) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
̂ |
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|||
Несмещенная оценку для дисперсии: |
2 |
= |
|
|
|
|
∑ |
( |
− ) |
= 53,61 |
||||||||||
|
|
|
|
|
=1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4.
Найдем доверительный интервал для математического ожидания (дисперсия известна):
1
̅ = ∑
=1
М[ ̅] = m = 1 ∑=1 [ ] = 3,77
, , отсюда следует, что D[ ̅] = 1,05
√ = 1,03
Доверительный интервал для математического ожидания:
m − |
σ |
< m ′ < m + |
σ |
|
|||
|
|
|
|
||||
x |
√N |
x x √ |
N |
|
|||

Ф( ) = 2 = 0,45 => = 1,645
Подставим и получим: 3,53< m′x < 4,01
Найдем доверительный интервал для математического ожидания (дисперсия
неизвестна): mx − t √N̂ < mx′ < mx + t √N̂
̂2 = 1−1 ∑ =1( − ̅)2 => ̂ = 7,32
При = 0,90, N= 50: t = 1,675 (по таблице критических точек распределения Стьюдента).
Подставим и получим: 2,04< m′x < 5,50
5.
2 < 1,2 = 1−2 = 0.05 ,
2 < 2,2 = 1+2 = 0.95
Т.к. объём выборки более 30, то будем использовать асимптотическую формулу:
Квантили нормального распределения равны: |
|
|
|
|
|
U 0.05 = −1.65, |
|
|
|
|
|
U 0.95 = 1.65 |
|
|
|
|
|
Подставим в форулу и получим: 2 |
= 33,89, 2 |
= 66,4 |
|
|
|
1, |
|
2, |
|
|
|
|
|
̂2 |
|
|
̂2 |
Доверительный интервал найдем по формуле |
( −1) |
< 2 < |
( −1) |
||
2 |
2 |
|
|||
|
|
1− |
|
1+ |
|
|
|
2 , −1 |
|
2 |
, −1 |
Подставим и получим: 6,29< < 8,80
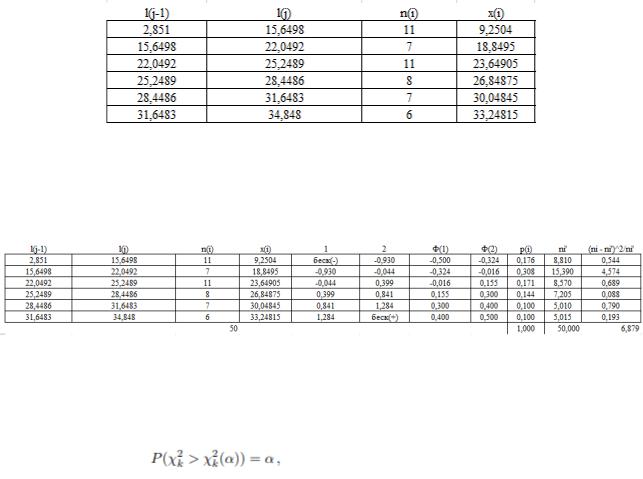
6.
Объединим интервалы:
Теоретические частоты: ′ = |
|
|
|
− ̅ |
|
|
|
−1 |
− ̅ |
|||
= (Ф |
|
( |
|
) − Ф |
|
( |
|
|
) ) |
|||
0 |
|
0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Построим таблицу с параметрами для новых интервалов:
Наблюдаемое значение критерия равно: ( 2) = |
∑=16 |
( −′)2 |
|
|
|
|
= 6,879 |
||
′ |
|
|||
|
|
|
|
|
|
|
|
|
|
Строим правостороннюю критическую область, удовлетворяющую неравенству:
k = s − 3 = 6 – 3 = 3, тогда 32(0,1) = 6,251
Вывод: Наблюдаемое (эмпирическое) значение критерия ( 2) = 6,879 и
попадает в критическую область: ( 2) > 42(0,1). Гипотеза о равномерном распределении генеральной совокупоности при уровне значимости α = 0.1
должна быть отвергнута. Данные выборки распределены не по нормальному закону
