
- •1Московский технический университет связи и информатики
- •1. Задание на курсовую работу
- •1.1. Анализ цепи по постоянному току
- •1.2. Анализ цепи при гармонических функциях источников во временной области
- •1.3.Анализ цепи при гармонических функциях источника в комплексной области
- •1.4. Построение частотных характеристик входного сопротивления и передаточной функции
- •1.4.2. Проверить частотные характеристики входного сопротивления и передаточной функции, используя программу схемотехнического моделирования micro-cap.
- •1.4.3. Полученные частотные характеристики объяснить с помощью эквивалентных моделей схемы, которая была взята в пункте 1.4.1.1.
- •2.Курсовая работа
- •1.1. Анализ цепи по постоянному току
- •1.2. Анализ цепи при гармонических функциях источников во временной области
- •1.3.Анализ цепи при гармонических функциях источника в комплексной области
- •1.3.1. Перевести схему цепи из временной области в комплексную. Привести рисунок схемы в соответствующих обозначениях.
- •1.4.2. Проверить частотные характеристики входного сопротивления и передаточной функции, используя программу схемотехнического моделирования micro-cap.
- •3.Вывод
- •4.Список используемых источников

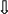
Параметры
Вариант
|
R1,
Ом |
R2,
Ом |
R3,
Ом |
L1,
Гн |
L2,
Гн |
L3,
Гн |
С1, Мк Ф |
С2, Мк Ф |
С3 Мк Ф |
F ,
Гц |
e1(t), В |
e2(t), В |
e3(t), B |
8, 18, 28 |
15 |
70 |
45 |
7.0 |
5.8 |
10.0 |
2.9 |
3.9 |
0.1 |
420 |
16SIN(ωt+61) |
34SIN(ωt-85) |
12SIN(ωt+41) |
1.1. Анализ цепи по постоянному току
Для получения схемы цепи постоянного тока необходимо приравнять значение частоты в выражениях е1(t), e2(t), e3(t) нулю.
Полученное значение для ЭДС источников определить их, как источники постоянной ЭДС – E1, E2, E3.
Привести эквивалентные схемы цепи постоянного тока в двух случаях - при подключении источников и при t→∞.
е1(t) = 16SIN(ωt+61)
e2(t) = 34SIN(ωt-85)
e3(t) = 12SIN(ωt+41)
E1 = 16SIN(61) = -15.458
E2 = 34SIN(-85) = 5.987
E3 = 12SIN(41) = -1.903
При t→∞ на конденсаторах возникает разрыв




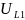 =17.361B
=17.361B
 =-17.361B
=-17.361B
 =-21.445В
=-21.445В
При t→0 на катушках возникает разрыв






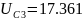
1.2. Анализ цепи при гармонических функциях источников во временной области
Привести схему электрической цепи во временной области.
Составить необходимое и достаточное число уравнений цепи, применяя метод уравнений Кирхгофа.
Составить необходимое и достаточное число уравнений, применяя метод контурных токов.
Составить матрицы коэффициентов и правых частей уравнений.
Записать решение для токов в виде матричного соотношения.
УКАЗАНИЕ. Решение систем уравнений относительно неизвестных мгновенных токов не проводить.
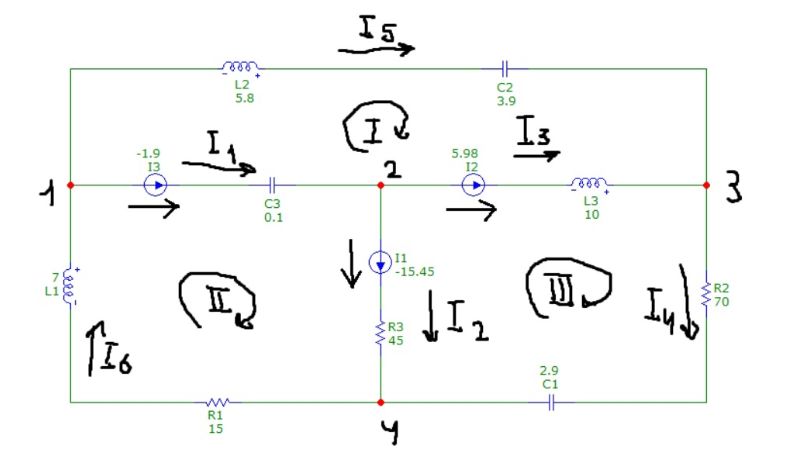
В схеме 3 контура, 4 узла, 6 ветвей
1ый закон Киргхофа: 4-1=3

-

2ой закон Киргхофа: 6-4+1=3
1ый контур:


2ой контур:


3ий контур:

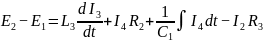
Метод контурных токов:
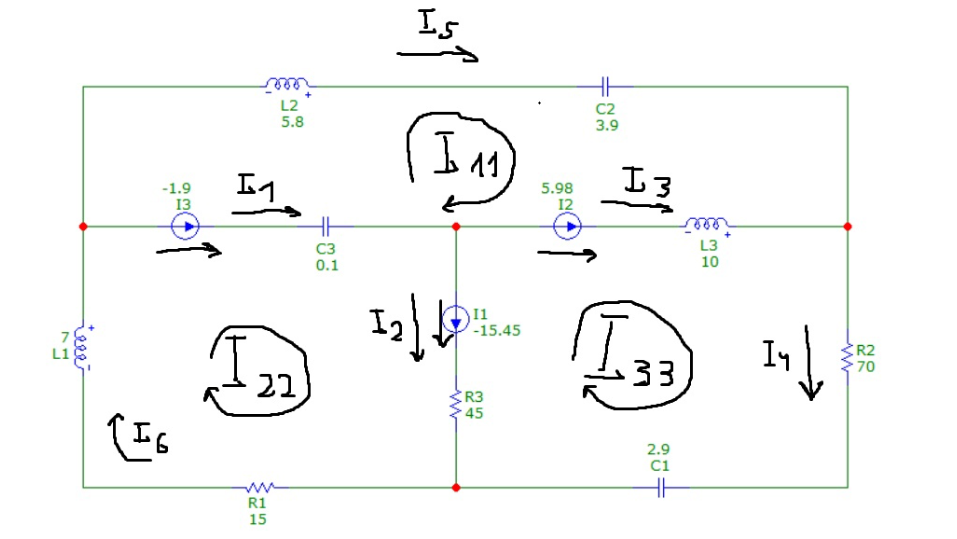


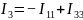
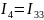

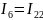
1ый контур:
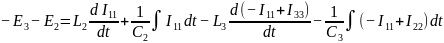
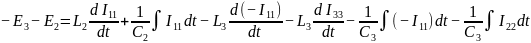
2ой контур:


3ий контур:


Матрицы коэффициентов:
1)
1 |
0 |
0 |
0 |
1 |
1 |
-1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
-1 |
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
0 |
0 |
|
0 |
|
|
|
0 |
0 |

2)
|
|
|
|
|
|
|
|
|
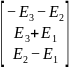
1.3.Анализ цепи при гармонических функциях источника в комплексной области
1.3.1. Перевести схему цепи из временной области в комплексную. Привести рисунок схемы в соответствующих обозначениях.

 Ом
Ом
 Гн
Гн
 МкФ
МкФ
F = 420 Гц
 Ом
Ом
 Ом
Ом
 Ом
Ом
 Ом
Ом
 Ом
Ом
 Ом
Ом
Сопротивление узлов:
|
|
|
|
|
26486.46j Ом |
|
|
|
|
|
|
|
|
|
|
|
|
1.3.2. Перевести, полученные матричные уравнения в предыдущем пункте для метода уравнений Кирхгоффа и метода контурных токов, в комплексную форму
По Киргхофу
-
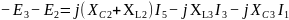
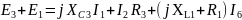

По контурным токам

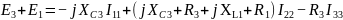

1.3.3. Составить необходимое и достаточное число уравнений по методу узловых потенциалов в комплексном виде.
Допустим
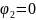



 .
.

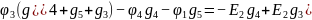
1.3.4. Записать все три системы уравнений в матричной форме.


Киргхоф
Z=
E=
Метод контурных токов
Z=
E=
Метод узловых потенциалов
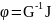
G= (столб
1-
(столб
1- ,
2-
,
2-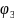 ,3-
,3- )
)
J=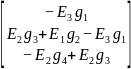
1.3.5. Решить две любые из систем. На основе полученного решения провести полный анализ схемы (определение токов всех ветвей и напряжений на всех элементах).
1)


2)



1.3.6. Перевести результаты анализа во временную форму.
Результаты в экспоненциальной форме:





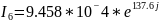


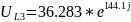
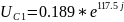



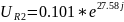

Результаты во временной форме











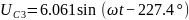
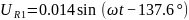


1.3.7. Построить на комплексной плоскости векторную диаграмму напряжений путём обхода контура (по выбору студента) и убедиться в выполнении 2-го закона Кирхгоффа.



1.3.8. Определить сопротивления ветвей этого контура и построить их на комплексной плоскости в виде векторных диаграмм.
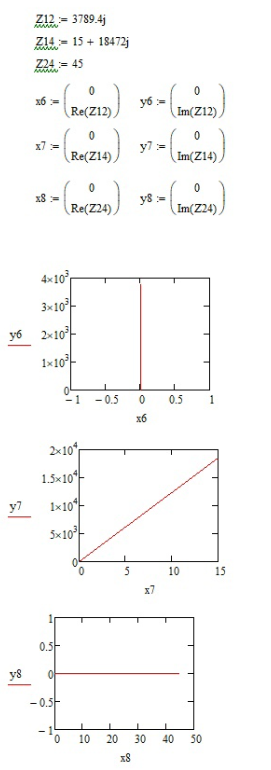
1.4. ПОСТРОЕНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ВХОДНОГО СОПРОТИВЛЕНИЯ И ПЕРЕДАТОЧНОЙ ФУНКЦИИ
1.4.1. ПРЕОБРАЗОВАТЬ исходную схему электрической цепи
1.4.1.1 - исключить источники напряжения e1(t), e2(t), e3(t)

1.4.1.2 - преобразовать в схеме «звезду» в «треугольник».


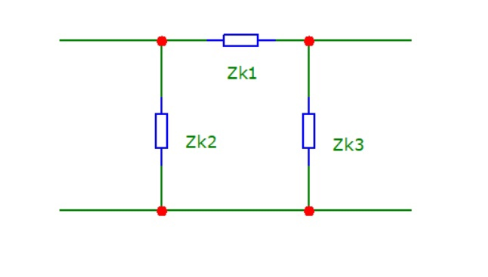

1.4.2. Получить формулы для входного сопротивления со стороны узлов 1, 4, а также выражение для передаточной функции на узлах 3,4.
Получение этих выражений следует провести с помощью пакета MATHCAD.
Входное сопротивление
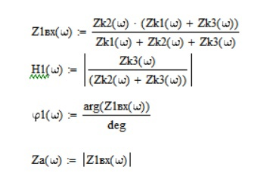
Выражение для передаточной функции
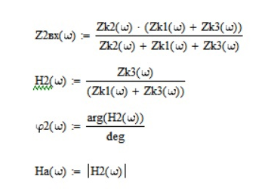
1.4.3. Построить частотные характеристики по полученным выражениям входного сопротивления и передаточной функции в указанном пакете программ.
Первый диапазон частот брать от нуля до до 5000 рад/с. Провести уточнение диапазона частот каждому студенту индивидуално с целью представления частотных характеристик наиболее информативно.
Графики АЧХ и ФЧХ делать в едином масштабе для совмещения и изучения хода кривых в локальных экстремумах.
Входное споротивление


Передаточная функция
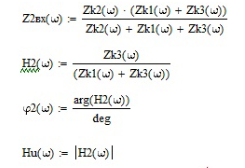
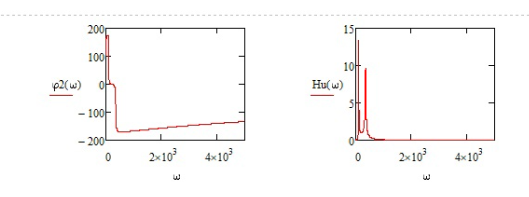
1.4.2. Проверить частотные характеристики входного сопротивления и передаточной функции, используя программу схемотехнического моделирования micro-cap.
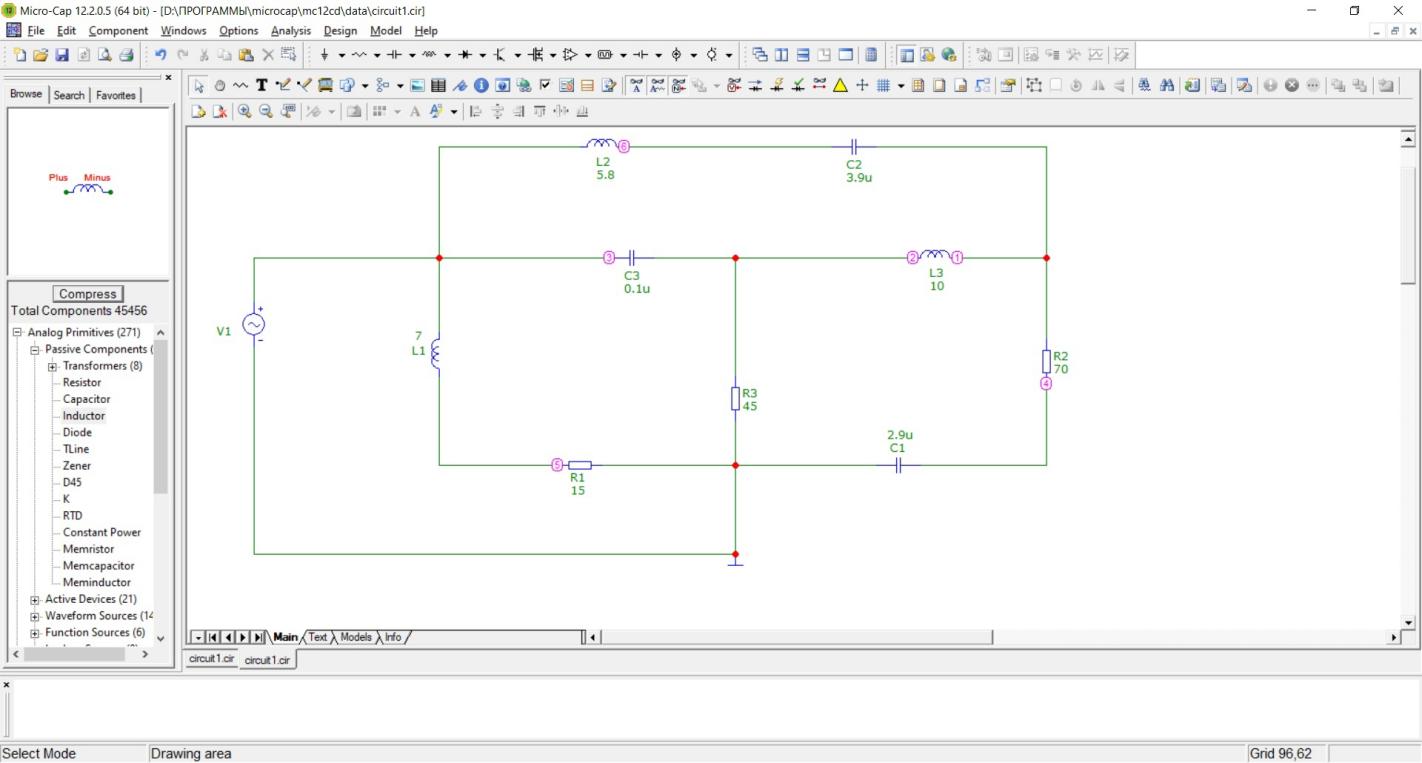
Входное
сопротивление
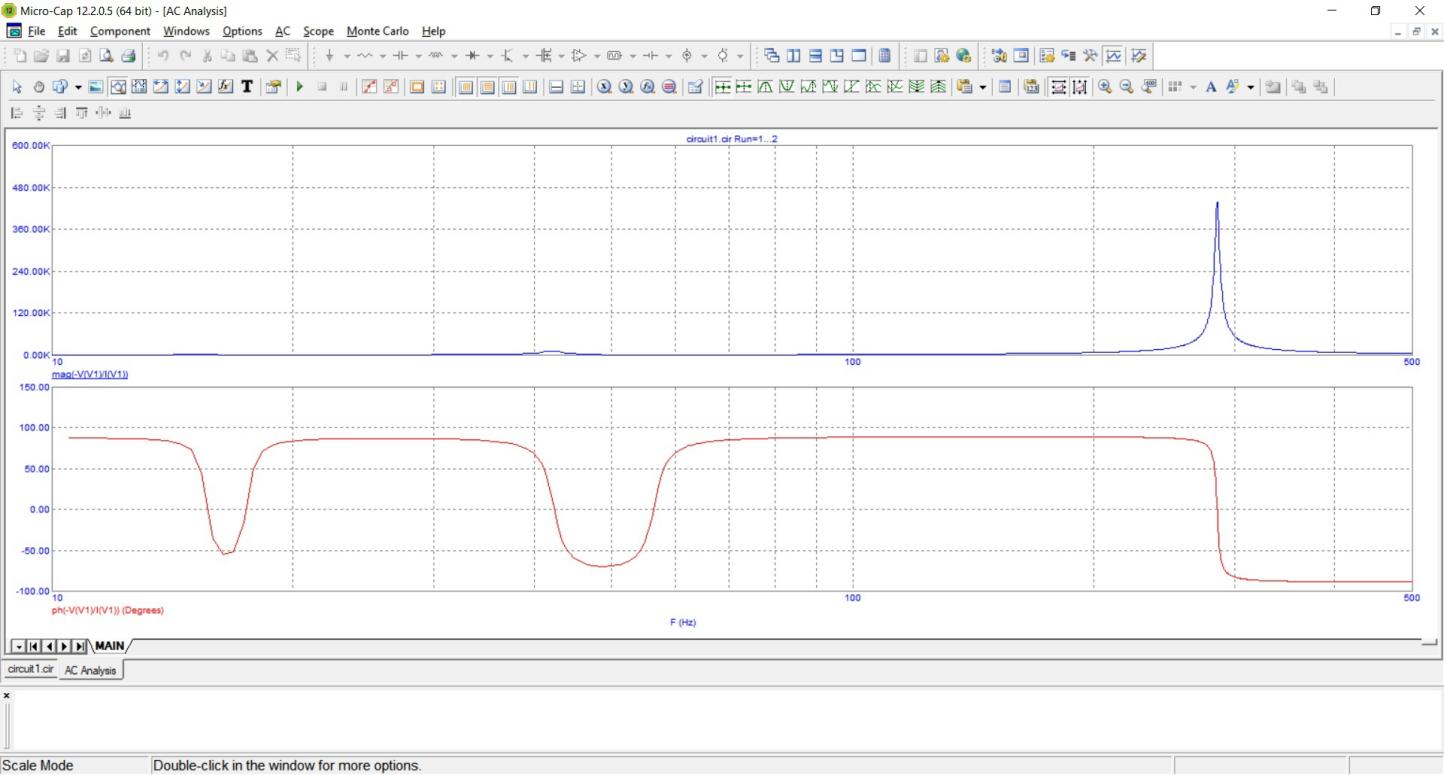
Передаточная функция

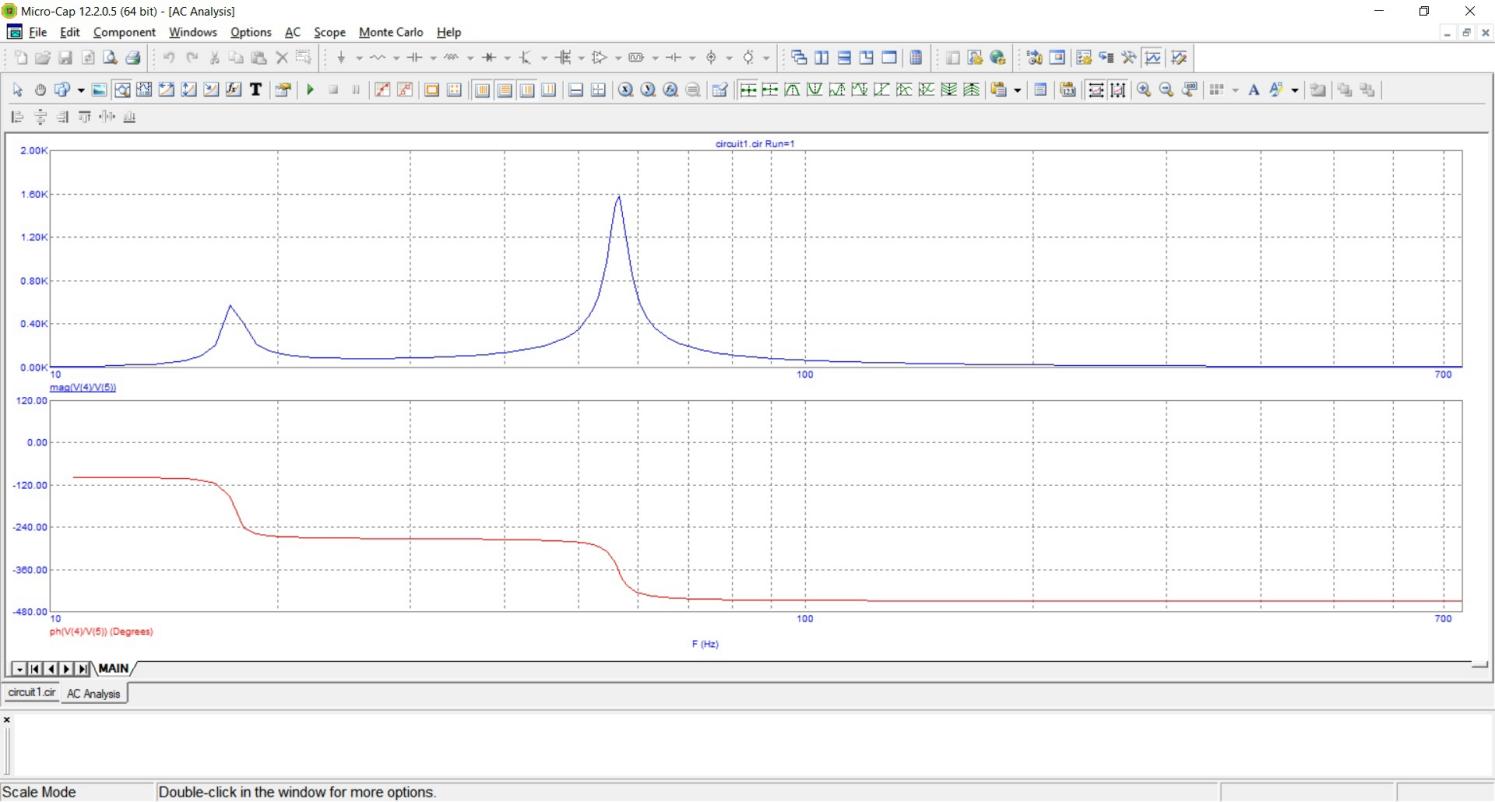
3.Вывод
Таким образом, в данной курсовой работе был проведен анализ электрической цепи.
Анализ электрической цепи включал в себя анализ цепи по постоянному току, в результате которого были приведены эквивалентные схемы цепи постоянного тока в двух случаях. Также был проведен анализ цепи при гармонических функциях источников во временной области путем приведения электрической цепи во временную область, вместе с тем и составления уравнений по методу уравнений Кирхгоффа и методу контурных токов. Следом, провели анализ цепи при гармонических функциях источников в комплексной области, который заключался в переводе схемы цепи из временной области в комплексную и, соответственно, матричных уравнений по методу уравнений Кирхгоффа и методу контурных токов. Также были составлены уравнения по методу узловых потенциалов в комплексном виде и решены две системы уравнений, одной из которых является система уравнений по методу уравнений Кирхгоффа, другой – система уравнений по методу контурных токов. Все результаты анализа были переведены во временную форму, на основе которых была построена векторная диаграмма напряжений путем обхода контура на комплексной плоскости. С помощью этого были определены сопротивления ветвей контура, построены на комплексной плоскости в виде векторных диаграмм.
В завершении данной курсовой работы является построение частотных характеристик входного сопротивления и передаточной функции в указанном пакете программ – Mathcad, MicroCap.
4.Список используемых источников
Крейнделин В.Б., Григорьева Е.Д., Степанова А.Г. Теоретические основы электротехники: учебно–методическое пособие. – М.: Московский технический университет связи и информатики, 2021. – 68 c.
Добротворский И. Н. Теория электрических цепей: Учебник для техникумов — М.: Радио и связь, 1989. - 472 с: ил.


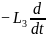
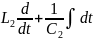
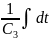





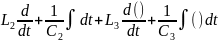






 j
Ом
j
Ом
 )
)

 +
+ Ом
Ом

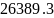 j
Ом
j
Ом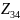
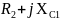
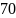 +
+ j
Ом
j
Ом
 Ом
Ом