Добавил:

VadoZ хачю сдать сессию Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский технический университет связи и информатики

Предмет:

Численные методы

Файл:

ЧМ пособие

.pdf

Скачиваний:

Добавлен:

01.06.2024

Размер:

2.37 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

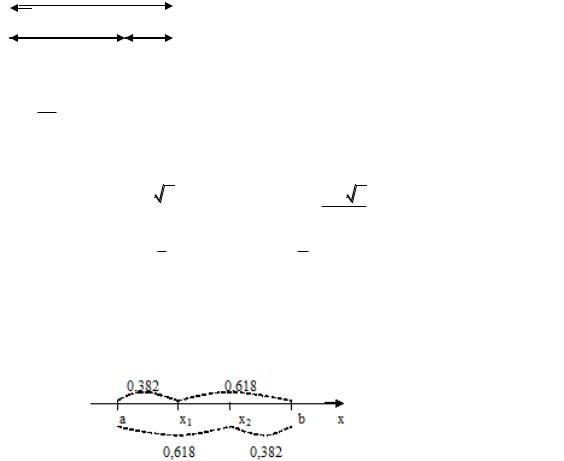
Метод прост, но достаточно трудоемок. Более эффективными являются другие методы одномерного поиска, в частности, метод дихотомии и метод золотого сечения и метод средней точки.

7.3. Метод дихотомии

Пусть дана функция f(x), унимодальная на отрезке [a;b]. Обозначим a0=a

и b0 = b.
Выберем на отрезке		[a0;b0] две точки симметричные относительно
середины отрезка:
α	a0 b0	δ	и β	a0 b0	δ,	0 δ	b a	,
α		δ	и β		δ,	0 δ		,
1	2		1	2		2
	2			2		2

где - параметр метода, истинную величину которого определим ниже. Вычислим и сравним значения функций f( 1) и f( 1). В силу

унимодальности функции можно провести сокращение отрезка неопределенности по следующему правилу:

Еслиf( 1) f( 1), то x* [a0; 1] ; Если f( 1) >f( 1), то x* [ 1;b0].

а)	b)
	Рис. 7.3-1

Если описанную процедуру принять за одну итерацию, то алгоритм поиска минимума можно описать следующим образом. Опишем (k+1)-ю итерацию, исходя из того, что k-й отрезок неопределенности найден [ak;bk]:

1.	Вычисляются α		ak bk	δ	и β		ak bk	δ.
1.	Вычисляются α			δ	и β			δ.
	k 1	2			k 1	2
		2				2
2.	Находят значения f( k+1) и f( k+1).
					61

3. Находят k+1-й отрезок неопределенности по правилу:

если f( k+1) > f( k+1), то x* [ k+1;bk], если f( k+1) f( k+1), то x* [ak; k+1]).

Сокращение отрезка					проводятся до тех пор, пока не выполнится
неравенство
	b a		ε ,			bn 1 an 1	δ,
n		n		n
	n				2

где n– длина n-го отрезка неопределенности.

От итерации к итерации n убывает и при n стремится к величине 2 . При некотором значении n выполняется условие bn-an<ε. Следовательно, достичь заданной точности можно лишь выбирая 0< /2.Таким образом, величина достаточно мала, и можно сказать, что на каждой итерации длина отрезка неопределенности сокращается практически в два раза.

Длину конечного интервала неопределенности, обеспечивающего заданную величину , можно вычислить по формуле

	0	2δ	2δ.
			2δ.

n		n
		2

Положив n= , можно определить соответствующее количество итераций:

n log	0	2δ	.


2	ε 2δ

Пример 7.3-1. Найти минимум функции f(x)=x3-x+e-х на отрезке [0;1]c точностью и вычислить количество итераций, требуемое для

обеспечения точности.

Выберем =0.001 и положим a = 0;b = 1;																		Δ0 1 0 1:
									1 0.002
1)		Если		ε 0.1,	то n log2											3.348				n 4.
1)		Если		ε 0.1,	то n log2											3.348				n 4.
									0.1			0.002
Длина				интервала				1 0.002					0.002 0.064375.
Длина				интервала		4	24						0.002 0.064375.
						4	24
												1 0.002
2)		Если		ε 0.01,		то n log2											6.963				n 7.
2)		Если		ε 0.01,		то n log2											6.963				n 7.
										0.01 0.002
Длина				интервала		7	1 0.002							0.002 0.009797.

							7
							2
																						Таблица 7.3-1
	n			an-1		bn-1					a1					b1			f(a1)			f(b1)	n
	1		0		1				0.499							0.501			0.23239			0.23067	0.501
	1		0		1				0.499							0.501			0.23239			0.23067	0.501
	2		0.499		1				0.7485							0.7505			0.14392			0.14435	0.2515
	2		0.499		1				0.7485							0.7505			0.14392			0.14435	0.2515
															62

	3	0.499		0.7505	0.62375	0.6257		0.15486		0.15413		0.12675
	3	0.499		0.7505	0.62375	0.6257		0.15486		0.15413		0.12675
	4	0.62375		0.7505	0.68613	0.6881		0.14040		0.14023		0.06437
	4	0.62375		0.7505	0.68613	0.6881		0.14040		0.14023		0.06437
	…	…..		…..	…..	….		…..		…..		….
	…	…..		…..	…..	….		…..		…..		….

	7	0.701719		0.71931	0.70951	0.7115		0.13954		0.13959		0.00979
	7	0.701719		0.71931	0.70951	0.7115		0.13954		0.13959		0.00979
При		= 0.1	x*=0.7183		f(x*)=0.1399,		а при		= 0.01		x*=0.7066

f(x*)=0.13951.

7.4. Метод золотого сечения

В основу метода положено разбиение отрезка неопределенности [a;b] в соотношении золотого сечения, такого, что отношение длины его большей части ко всей длине отрезка равно отношению длины его меньшей части к длине его большей части:

l


l	l	l2								l1
		l2								l1
										l l	l									l .
2	1	,где												,			и		l
		,где												,			и		l
l	l									1		2							2	1
l	l
	2
Положим l =1,			тогда l22 = 1 - l2 , а										l22 + l2 -1= 0, откуда
		l		1				5		0.618,	l	l l					3	5	0.382 ,
		l								0.618,	l	l l			2				0.382 ,
		2				2					1				2		2
						2											2
				k			l		0.382,			k			l	0.618,
				k			1		0.382,			k			2	0.618,
							1								2
					1		l						2		l
							l								l

где k1, k2 - коэффициенты золотого сечения.

В методе золотого сечения каждая точка (х1 и х2)осуществляет золотое сечение отрезка.

x		a	5 1			(b a) a k (b a),
x	1	a				(b a) a k (b a),
	1		2				1
			2
x		a	3	5			(b a) a k		(b a),
x	2	a	2				(b a) a k	2	(b a),
	2							2

k	1	0.382,		k	2		0.618,
	1				2

x		a 0.382(b a)
1
x	2	a 0.618(b a)
	2

или

x	1	a k (b a)
		1
x	2	a k	2	(b a)

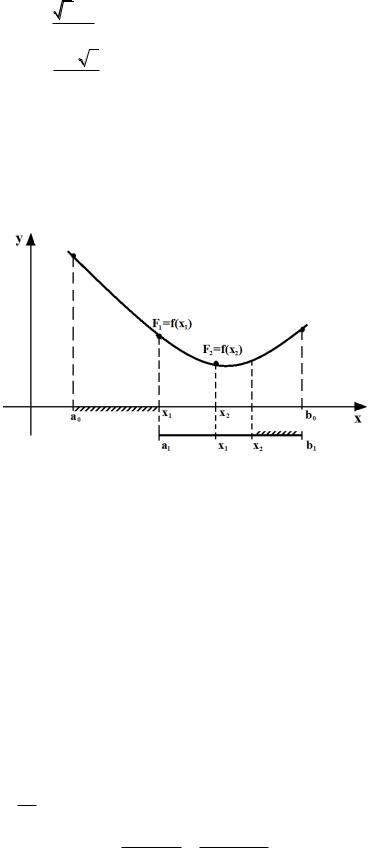
Геометрическая интерпретация метода золотого сечения приведена на рис. 7.4-1.

Рис. 7.4-1.

Нетрудно проверить, что точка х1 осуществляет золотое сечение не только отрезка [a;b], но и отрезка [a;х2]. Точно так же точка х2осуществляет золотое сечение не только отрезка [a;b], но и отрезка [х1;b]. Это приводит к тому, что значение целевой функции на каждой итерации (кроме первой) вычисляется один раз.

После каждой итерации длина отрезка неопределенности сокращается в 1.618 раза. Длина конечного отрезка неопределенности n = 0.618n 0, где

0= (b-a) – начальная длина отрезка.
Условие окончания процесса итераций		n . Отсюда можно найти
количество итераций, необходимое для достижения точки минимума:
	n
n	0.618	0

Отсюда 0.618n n ,

поэтому, логарифмируя, получим

n	lg(ε /	0	)	lgε lg	0	.
n						.

	lg0.618			lg0.618

Пример 7.4-1. Пусть минимум функции f(x) = x3 – x + e-x отделен на отрезке [0;1]. Определить количества итераций и конечные длины

отрезков неопределенности, необходимые для достижения заданных точностей =0.1 и =0.01.

				ε 0.1				n			lg0.1/1			1	4.76			n 5,
				ε 0.1				n			lg0.618		0.21		4.76			n 5,
											lg0.618		0.21
							0.618		5		0.618	5	1 0.0901 0.1;
					n		0.618				0.618		1 0.0901 0.1;
					n
			ε 0.01					n			lg0.01/1			2		9.52		n 10,
			ε 0.01					n			lg0.618			0.21		9.52		n 10,
											lg0.618			0.21
				n 0.61810							0.61810		1 0.0081 0.01.
																			Таблица 7.4-1
	N	a					b				x1			x2			f(x1)		f(x2)	n
	1	0				1				0.38196			0.61803				0.35628		0.15704	0.61803
	2	0.38196				1				0.61803			0.76393				0.15704		0.14772	0.382
	3	0.61803				1				0.76393			0.85410				0.14772		0.19462	0.236
	4	0.61803				0.85410				0.70820			0.76393				0.13953		0.14772	0.146
	5	0.61803				0.76393				0.67376			0.70820				0.14188		0.13953	0.090
При = 0.1			x*=0.718847,								f(x*)=0.139925.
При = 0.01			x=0.704139, f(x)=0.139516.

7.5. Метод средней точки

Алгоритм метода средней точки основан на сокращении длины текущего отрезка неопределенности [a;b], путем отбрасывания его части, не содержащей точки минимума. Как известно, для того чтобы на отрезке [a;b] существовал минимум, необходимо, чтобы первая производная на нем была неубывающей. Выбирается пробная точка, принадлежащая отрезку (как правило, середина


отрезка c=(a+b)/2), и если	f (c) 0	, то в следствии унимодальности функции

точка минимума не может лежать левее точки с, а если			f (c) 0	, то не может

лежать правее точки с.

Пусть на отрезке [a;b] отделен единственный минимум функции f(x). Требуется определить значение точки минимума с заданной точностью .

Рассмотрим алгоритм поиска минимума по шагам:

					f			) 0
1.	Положим i=0, ai=a, bi=b причем				f	(a		) 0	, а		)	0 .
1.	Положим i=0, ai=a, bi=b причем						i		, а	f (bi	)	0 .
2.	Вычислим	c	ai bi
		c
		2		и f (c) .
		2
3.
3.	Если f (c) , то поиск закончен и следует перейти к шагу 4.

4. Если f (c) 0 , то положить ai+1=с, bi+1=bi, i=i+1 и перейти к шагу 2.

Если	f (c) 0	, то положить

шагу 2.
5. Вычислить X min			ai bi	и	f min

		2


bi+1=с,		ai+1=ai, i=i+1 и перейти к
f ( X	min		)	.

Поскольку на каждой итерации отрезок унимодальности сокращается в два раза, то очевидно, что после некоторой n-й итерации длина отрезка [a;b]

вычисляется как

	n

		b a
		2	n

. Однако этот метод имеет существенный недостаток

- вычисление производной от целевой функции.

Пример 7.5-1. Выполнить две итерации по нахождению минимума

функции	f (x) 2x	2	16

			x

отрезке [1;5].

1-я итерация:

методом средней точки, если минимум отделен на

1.	a0=1, b0=5,							16		,	f		12	и	f		19.36
									2
						f (x) 4x		x	2			(1)				(5)
								x
2.	c		a		b	1 5	3.
2.	c			0	0		3.
				0	0
					2	2
3.	f				10.22 0		, следовательно, a1=a0=1; b1=c=3.
3.	f	(3)			10.22 0		, следовательно, a1=a0=1; b1=c=3.

2-я итерация:

2.	c	a	b	1 3	2.
2.	c	1	1		2.
		1	1
			2	2

f (2)

, следовательно, a2=a1=1; b2=c=2.

Тема 8. Многомерная оптимизация

8.1. Постановка задачи и основные определения

Задача, требующая нахождения оптимального значения функции m переменных f(Х)=f(x1, x2, …, xm), называется задачей многомерной оптимизации. Так же, как и для случая одномерной оптимизации, задача нахождения максимума функции сводится к задаче нахождения минимума путем замены целевой функции f на -f.

Пусть функция f(Х) = f(x1, x2, …, xm) определена на некотором множестве Х Rm. Если Х=Rm (т.е. ограничения на переменные x1, x2, …, xm отсутствуют), принято говорить о задаче безусловной минимизации. В противном случае, когда Х Rm, говорят о задаче условной минимизации.

Методы решения задачи безусловной минимизации являются основой для перехода к изучению более сложных методов решения задач условной минимизации.

В постановке задачи безусловной оптимизации для f(Х)=f(x1, x2, …, xm) требуется найти хотя бы одну точку минимума Х* и вычислить f*=f(Х*).Точка Х* Rm называется точкой глобального минимума функции fна множестве Х, если для всех Х Rm выполняется неравенство f(Х*) f(Х). В этом случае значение f(Х*) называется минимальным значением функции на Rm.

Точка Х* Rm называется точкой локального минимума функции, если существует такая - окрестность U этой точки ( >0), что для всех Х Х =Х U выполняется неравенство f(X*) f(X).

Подавляющее большинство методов решения задачи безусловной минимизации в действительности являются методами поиска точек локальных минимумов, среди которых затем выделяют глобальный минимум, являющийся наименьшим. Этот способ очень трудоемок, поэтому чаще используют другой: местоположение точки глобального минимума определяют в ходе анализа решаемой задачи, а затем для его уточнения с заданной точностью применяют один из методов поиска точки локального минимума. Рассмотрим функцию нескольких переменных и введем для нее основные определения.

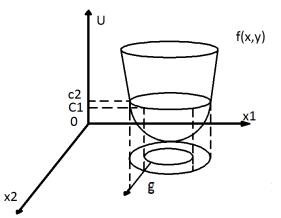
Множество точек, для которых целевая функция принимает постоянное значение f(x1, x2, …, xm) = c, называется поверхностью уровня. Для функции двух переменных (m = 2) это множество называется линией уровня.

Функция f(x1,x2) задает в трехмерном пространстве некоторую поверхность U= f(x1,x2) (рис. 8.1-1), низшая точка которой и дает решение задачи минимизации. Для того чтобы изобразить рельеф этой поверхности, проведем несколько плоскостей (U = const): U=c1, U=c2, U=c3 . Проекции на плоскость Ох1х2 линий пересечений этих плоскостей с поверхностью и дают линии уровня

Рис. 8.1-1

Для дифференцируемой функции можно определить вектор из первых частных производных, который называется градиентом grad(f(x)) :



	f(x)
	x
		1
	f(x)
grad(f(x)) f '(x)	f(x)		(8.1-1)
grad(f(x)) f '(x)	x2		(8.1-1)


	...
	f(x)
	x
	x
		m

Направление вектора градиента

grad(f(x))

указывает

направление

наискорейшего возрастания функции, а его модуль (длина) равен скорости возрастания функции. Градиент нормален к линии уровня в каждой своей точке и касателен к поверхности, которую задает функция.

Вектор - grad(f(x)) называется антиградиентом и показывает направление наискорейшего убывания функции.

Равенство нулю градиента в точке Х является необходимым условием того, чтобы внутренняя для множества Хi (i = 1, 2,…m) точка Х была точкой локального минимума дифференцируемой функции f. Точка Х, для которой выполняется равенство f’(X) = 0, называется стационарной точкой функции.

Это равенство представляет собой систему из m нелинейных уравнений относительно компонент х1, х2, …, хm, вектора X, где m – количество переменных.

f(x1,x		2,...,xm ) 0
	x1
	x1

	f(x ,x		,...,x		)	0
	1	2		m		0
	x2
..............................
	f(x1, x
	f(x1, x	2,...,xm ) 0
	xm
	xm					(8.1-2)
						(8.1-2)

Для функции двух переменных Q(x, y)это условие имеет вид:

Q(x, y)
	x
	x
	Q(x, y)
	Q(x, y)
	y

(8.1-3)

Однако не всякая стационарная точка является точкой минимума. Для всякой непрерывно дифференцируемой функции f достаточным условием того,

чтобы стационарная точка Х была точкой локального минимума, является положительная определенность матрицы вторых производных (матрицы Гессе):

			2			f					2		f
			2								2
	x					2	...	x x
	x							x x
					1				1						m
			2			f					2		f
						f	...						f
G(x) f (x)	x			x			...	x			x
G(x) f (x)	x	2		x				x	2		x				m
		2				1			2						m
	...						...		...
	...						...		...
						f								f
			2			f						2		f
			2									2
	x				x		...	x				x
	x	m			x			x		m		x				m
		m				1				m						m

(8.1-4)

Согласно критерию Сильвестра, для того чтобы матрица была положительно определена, необходимо, чтобы все угловые миноры были положительны:

			a		a					...		a
				11			12							1m
A			a	21	a		22			...		a		2m
A

			... ... ... ...
			a	m1	a			m2		...		a			mm
				m1				m2							mm
	1	a			0,
	1		11
	2	a			a	22			a		a		21			0	и	т.д.
	2			11		22				12			21

(8.1-5)

Для функции двух переменных Q(x, y) матрица Гессе имеет вид:

		Q
	2
	x
		2
G(x,y)		Q
	2
	y x

	Q
2
x y
	Q
2
y
	2

(8.1-6)

а достаточное условие существования минимума:

		Q
	2
				2		0,
1	x			2
	x
			Q					Q			Q	2
	2						2			2
2	x				2		y		2			0.
	x						y			x y

(8.1-7)

Алгоритм решения задачи оптимизации функции двух переменных Q(x,y) аналитическим (классическим) методом следующий:

1. Составляется и решается система уравнений

		Q(x,y)	0;
		x	0;
		x


		Q(x,y)
		Q(x,y)	0,
		y	0,
		y

из которой находятся (x*, y*)

2. Проверяются достаточные условия существования минимума

		2
		Q(x,y)			0
			x	2	0
				2

2		2				2	2
Q(x,y)		Q(x,y)				Q(x,y)
x	2	y	2			x y	0.
	2		2

Если (x*, y*) – единственное решение и в этой точке выполняются достаточные условия, то это точка минимума. Если хотя бы в одном из неравенств получается знак ―<‖, то минимума не существует. В случае появления знака ―=‖ необходимо исследовать производные высших порядков.

Пример 8.1-1. Найти точку локального минимума функции.

f(x,y) =					x2 + y2 – 4x + 100 – 8y.
f			2x		4,
	x		2x		4,			2x 4 0,

													x	2;y	4.
	f								2y	8 0,			x	2;y	4.
	f		2y		8,				2y	8 0,
	y		2y		8,
	y

		f					f					f
	2					2					2
x		2	2;		y		2	2;			x y		0.
x					y						x y

2			0	,	2 0;						4 0 4 0.
				,	2 0;					2	4 0 4 0.
0			2		1					2
0			2

Следовательно, в точке x*=2 и y*=4 функция имеет локальный минимум.

Пример 8.1-2. Найти точку локального минимума функции f(x,y)= x2+y2–4x+10xy–8y.

f		2x 4 10y,
	x	2x 4 10y,	2x 4 10y 0,


	f			8 10x	0.
	f	2y 8 10x,	2y	8 10x	0.
	y	2y 8 10x,

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в предмете Численные методы

#
01.06.20243.75 Mб4Алгоритмы пособие.pdf
#
01.06.202429.98 Mб0ГОСТ.pdf
#
01.06.202423.44 Кб1Из ГОСТ Оформление научной работы ОТЧЕТА.docx
#
01.06.2024226.19 Кб0ЛР3 Аппрокс - МНК.docx
#
01.06.20242.37 Mб3ЧМ пособие.pdf