
ЧМ пособие
.pdf
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
Московский технический университет связи и информатики
Т.И.Семенова, О.М.Кравченко, В.Н.Шакин
Вычислительные модели и алгоритмы решения задач
численными методами
Учебное пособие
для направления
11.03.02– Инфокоммуникационные технологии
исистемы связи
Москва 2017
УДК32.973.26018.2
Семенова Т.И., Кравченко О.М., Шакин В.Н. Вычислительные модели и алгоритмы решения задач численными методами. Учебное пособие/ МТУСИ. – М., 2017. – 85с.
Учебное пособие содержит краткое теоретическое описание наиболее часто используемых в инженерной практике и в современных математических пакетах прикладных программ численных методов и методов оптимизации.
Ил. 29, табл. 18, список лит . 9 назв.
Издание утверждено советом факультета . Протокол № от
Рецензенты:
© Московский технический университет связи и информатики, 2017
2
Оглавление
Введение .................................................................................................................................. |
5 |
Тема 1. Элементы теории погрешностей ........................................................... |
5 |
1.1. Точные и приближенные числа.............................................................. |
5 |
1.2. Абсолютная и относительная погрешность....................................... |
6 |
Тема 2. Методы решения нелинейных уравнений................................... |
8 |
2.1. Постановка задачи........................................................................................ |
8 |
2.2. Отделение корней......................................................................................... |
9 |
2.2.1. Графическое отделение корней........................................................... |
10 |
2.2.2. Аналитическое отделение корней...................................................... |
11 |
2.3. Уточнение корней........................................................................................ |
12 |
2.3.1. Метод половинного деления .......................................................... |
12 |
2.3.2. Метод итерации ...................................................................................... |
13 |
2.3.3. Метод Ньютона (метод касательных) ............................................ |
17 |
2.3.4. Метод хорд................................................................................................. |
19 |
Тема 3. Интерполяция функций............................................................................. |
22 |
3.1. Постановка задачи .................................................................................... |
22 |
3.2. Интерполяционная формула Лагранжа ............................................ |
24 |
3.3. Интерполяционные формулы Ньютона ............................................. |
27 |
3.3.1. Конечные разности .................................................................................. |
27 |
3.3.2. Первая интерполяционная формула Ньютона....................... |
29 |
3.3.3. Вторая интерполяционная формула Ньютона .............................. |
31 |
3.4. Сплайн – интерполяция ........................................................................... |
33 |
Тема 4. Аппроксимация функций ......................................................................... |
34 |
4.1. Постановка задачи аппроксимации.................................................... |
34 |
4.2. Метод наименьших квадратов............................................................... |
35 |
Тема 5. Численное интегрирование .................................................................... |
40 |
5.1. Постановка задачи...................................................................................... |
40 |
5.2. Методы прямоугольников........................................................................ |
41 |
5.3. Формула трапеций ...................................................................................... |
42 |
5.4. Формула Симпсона...................................................................................... |
43 |
5.5. Оценка погрешности численного интегрирования ..................... |
44 |
Тема 6. Методы решения обыкновенных дифференциальных
уравнений.............................................................................................................................. |
47 |
6.1. Постановка задачи...................................................................................... |
47 |
6.2. Метод Эйлера ................................................................................................ |
49 |
6.3. Методы Рунге-Кутты................................................................................... |
51 |
6.4. Решение ОДУ n-го порядка..................................................................... |
55 |
|
3 |
Тема 7. Одномерная оптимизация........................................................................ |
57 |
7.1. Постановка задачи...................................................................................... |
57 |
7.2. Метод прямого перебора с переменным шагом ............................ |
60 |
7.3. Метод дихотомии ......................................................................................... |
61 |
7.4. Метод золотого сечения ........................................................................... |
63 |
7.5. Метод средней точки ................................................................................. |
65 |
Тема 8. Многомерная оптимизация ..................................................................... |
66 |
8.1. Постановка задачи и основные определения................................ |
66 |
8.2. Методы спуска............................................................................................. |
71 |
8.3. Метод градиентного спуска с дроблением шага .......................... |
72 |
8.4. Метод наискорейшего спуска................................................................ |
74 |
8.5. Метод покоординатного спуска........................................................... |
76 |
Тема 9. Методы решения систем линейных уравнений....................... |
79 |
9.1. Постановка задачи...................................................................................... |
79 |
9.2.Метод Гаусса ................................................................................................... |
80 |
9.3. Метод итераций............................................................................................ |
82 |
Список литературы.......................................................................................................... |
85 |
4
Введение
Широкое распространение персональных компьютеров и программных средств, в частности математических пакетов, позволяют решать многие трудоемкие и сложные задачи. Наличие готовых программных средств не только не снимает проблему обучения специалистов методам решения задач и обработки данных, а делает подготовку в этом направлении еще более актуальной. Это объясняется тем, что использование готовых программных средств, требует от специалиста грамотной математической постановки задачи, выбора эффективного метода решения и умения оценить погрешность результата. При решении реальных инженерных задач, когда мы имеем дело не только с приближенными результатами, но и с приближенными исходными данными, на первый план выступают не точные, а приближенные (численные) методы, которые зачастую позволяют получить решения даже в тех случаях, когда другие методы оказываются бессильны.
Тема 1. Элементы теории погрешностей
1.1. Точные и приближенные числа
Точность числа, как правило, не вызывает сомнений, когда речь идет о целых значениях данных(2 карандаша, 100 деревьев). Однако, в большинстве случаев, когда точное значение числа указать невозможно (например, при измерении предмета линейкой, снятии результатов с прибора и т.п.), мы имеем дело с приближенными данными.
Приближенным значением |
a * |
называется число, незначительно |
|
|
|
||
отличающееся от точного значения |
a |
и заменяющее его в вычислениях. Степень |
|
|
|||
отличия приближенного значения числа от его точного значения характеризуется погрешностью.
Различают следующие основные источники погрешностей:
1.Погрешности постановки задачи, возникающие в результате приближенного описания реального явления в терминах математики.
2.Погрешности метода, связанные с трудностью или невозможностью решения поставленной задачи и заменой ее подобной, такой, чтобы можно было применить известный и доступный метод решения и получить результат, близкий к искомому.
3.Неустранимые погрешности, связанные с приближенными значениями исходных данных и обусловленные выполнением вычислений над приближенными числами.
4.Погрешности округления, связанные с округлением значений исходных данных, промежуточных и конечных результатов, получаемых с применением вычислительных средств.
5

1.2. Абсолютная и относительная погрешность
Одной из основных задач теории погрешностей является оценка точности
результата на основании точности исходных данных. |
|
|
||||
Если |
a |
– точное число и |
a * |
– его приближенное значение, то |
||
погрешностью (ошибкой) приближенного значения |
a * |
является степень |
||||
близости его значения к его точному значению a . |
|
|
||||
Простейшей количественной мерой погрешности |
a * является абсолютная |
|||||
погрешность, которая определяется как |
|
|
|
|||
(a*) | a a* | .
(1.2-1)
Как видно из формулы 1.2-1, абсолютная погрешность имеет те же единицы измерения, что и величина a . Поэтому по величине абсолютной
погрешности далеко не всегда можно сделать правильное заключение о качестве приближения. Например, если (a*) 0.01 м , а речь идет о детали, вытачиваемой на станке, то измерения являются очень грубыми, а если о размере судна, то – очень точными. В связи с этим введено понятие относительной погрешности, в котором значение абсолютной погрешности отнесено к модулю приближенного значения ( a* 0 ).
δ(a*) |
| a a* | |
. |
|
| a* | |
|||
|
|
(1.2-2)
Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерений данных. Относительная погрешность измеряется в долях или процентах. Так, например,
если a* 0.3 |
,а (a*) 0.1, то |
δ(a*) 0.33 33% |
, а если |
a* 0.3 и (a*) 1.10 |
8 |
,то |
||||
|
||||||||||
тогда δ(a*) |
0.33 10 |
9 |
0.33 10 |
7 |
|
|
|
|
||
|
%. |
|
|
|
|
|||||
Чтобы численно оценить погрешность функции, требуется знать основные |
||||||||||
правила подсчета погрешности действий: |
|
|
|
|
||||||
|
при сложении и вычитании чисел абсолютные погрешности чисел |
|||||||||
|
складываются |
|
|
|
|
|
|
|||
|
|
|
|
|
|
(a b) (a) |
(b); |
|
|
|
|
при умножении и делении чисел друг на друга складываются их |
|||||||||
|
относительные погрешности |
|
|
|
|
|||||
|
|
|
|
|
|
δ(a b) δ(a) δ(b), |
|
|
|
|
δ(ba) δ(a) δ(b);
при возведении в степень приближенного числа его относительная погрешность умножается на показатель степени
δ(ak ) k δ(a).
6

Пример 1.2-1. Дана функция: y |
( |
a b |
|
) |
5 |
.Найти абсолютную |
||||||||
x(1 x) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
и относительную погрешности величины |
y |
|
(погрешность результата |
|||||||||||
выполнения арифметических операций), если значения |
(a), (b), (x) |
|||||||||||||
известны, а 1 – точное число и его погрешность равна нулю. |
|
|||||||||||||
δ(y) 5 | δ(a b) |
1 |
δ(x) δ(1 x) | 5 | |
(b) (a) |
|
1 |
|
(x) |
|
(1) (X) |
. |
||||
2 |
| a b | |
|
2 |
|
x |
| 1 x | |
||||||||
|
|
|
|
|
|
|
|
|||||||
Определив, таким образом, значение относительной погрешности, можно |
||||||||||||||
найти значение абсолютной погрешности, |
как |
(y) δ(y) y , |
где величина y |
|||||||||||
вычисляется по формуле при приближенных значениях a,b,x.
Поскольку точное значение величины a обычно неизвестно, то вычисление (a*) и δ(a*) по приведенным выше формулам невозможно. Поэтому на практике проводят оценку предельных погрешностей вида:
| a a* | (a*), |
||
| a a* | |
δ(a*), |
|
| a* | |
||
|
||
(1.2-3)
где |
(a*) и δ(a*) – |
границами абсолютной и предельная абсолютная образом, точное значение
известные величины, которые являются верхними относительной погрешностей, иначе их называют – и предельная относительная погрешности. Таким a лежит в пределах:
a * (a*) a a *
(a*)
или
a a * (a*).
Если величина |
(a*) |
величина |
δ(a*) , то |
(a*) | a* |
известна, то δ(a*) (a*) / | a* | , а если известна | δ(a*).
Предельная абсолютная погрешность функции вида
f(x ,x |
2 |
,...,x |
m |
) |
1 |
|
|
,
дифференцируемой в заданной области, при известных значениях аргументов x *1,x *2,...,x *m , а также при известных предельных абсолютных погрешностях
аргументов Δ(x*1), Δ(x*2 ), , Δ(x*m ) , вычисляется по формуле:
|
|
m |
|
|
|
||
|
|
(f ) |
|
(xi *) | |
f(x1*, x2 *,..., xm *) |, |
(1.2-4) |
|
|
x |
||||||
|
|
i 1 |
|
|
|||
|
|
|
|
|
|||
а, соответственно, предельная относительная погрешность функции
δ(f ) |
(f ) |
(1.2-5) |
| f(x1*,x2 *,...,xm *) | . |
В частном случае для функции от одной переменной (при m=1):
7

|
(f ) (x*) | f '(x*) |, |
||
|
δ(f ) |
(f ) |
. |
|
| f(x*) | |
||
|
|
|
|
Пример 1.2-2. Оценить абсолютную и относительную погрешности |
|||
приближенного числа |
e . |
|
|
Число |
e |
– |
трансцендентное |
число, |
представляется |
||||
непериодической дробью |
e 2.71828 |
. |
|
|
|
||||
|
|
|
|
|
|||||
Приближенное значение числа e* 2.7 . |
|
|
|||||||
Граница |
|
абсолютной |
погрешности |
| e e* | 0.019 |
, |
||||
погрешность числа |
δ(e*) | e e* | / | e* |, |
δ(e*) 0.007. |
|
||||||
бесконечной
относительная
Пример 1.2-3. Определить значащие цифры числа.
Значащими цифрами числа |
a * |
называют все цифры в его записи, |
начиная с первой ненулевой слева. Значащую цифру числа a * называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.
Значащие цифры чисел подчеркнуты:
Пример 1.2-4. Определить верные цифры подчеркнуть.
числа
a
356.78245
и
Если
Если
Если
Если
(a*) 0.01, то верных цифр в числе 5: |
a 356.78245. |
|
(a*) 0.3 ,то верных цифр в числе 4: |
a 356.78245. |
|
(a*) 0.0001, то верных цифр в числе 7: |
a 356.78245. |
|
(a*) 0.000001, то верных цифр в числе 8: |
a 356.78245. |
|
Тема 2. Методы решения нелинейных уравнений
2.1. Постановка задачи
Одной из важнейших и наиболее распространенных задач математического анализа является задача определения корней уравнения с одним неизвестным, которое в общем виде можно представить как f(x) = 0. В зависимости от вида функции f(x)различают алгебраические и трансцендентные уравнения. Алгебраическими уравнениями называются уравнения, в которых значение функции f(x) представляет собой полином n-й степени:
f(x) = Р(х) = anxn + a2x2 + …+ a1x + a0 = 0. |
(2.1-1) |
8 |
|

Всякое неалгебраическое уравнение называется трансцендентным уравнением. Функция f(x)в таких уравнениях представляет собой хотя бы одну из следующих функций: показательную, логарифмическую, тригонометрическую или обратную тригонометрическую.
Решением уравнения f(x)=0называется совокупность корней, то есть такие
|
|
|
|
|
|
|
|
|
значения независимой переменной x , |
при которых уравнение обращается в |
|||||||
тождество f(x) 0 . |
|
|
|
|
||||
Задача нахождения корня уравнения с заданной точностью |
ε |
(ε >0) |
||||||
считается решенной, если вычислено |
приближенное значение |
x |
, которое |
|||||
отличается от точного значения корня ξ |
не более чем на значение |
|
|
|
||||
|
|
|
|
|
||||
| ξ x | ε. |
|
(2.1-2) |
||||||
Процесс нахождения приближенного корня уравнения состоит из двух |
||||||||
этапов: |
|
|
|
|
||||
1) отделение корней (локализация корней); |
|
|
|
|||||
2) уточнение корней. |
|
|
|
|
||||
На этапе отделения корней решается задача отыскания возможно более узких отрезков [α;β] , в которых содержится один и только один корень уравнения.
Этап уточнения корня имеет своей целью вычисление приближенного значения корня с заданной точностью. При этом применяются итерационные методы вычисления последовательных приближений к корню: x0, x1, ..., xn, …, где каждое последующее приближение xn+1вычисляется на основании предыдущего xn. Каждый шаг называется итерацией. Если последовательность x0, x1, ..., xn, …при n имеет предел, равный значению корня ξ , то говорят, что итерационный процесс сходится.
2.2. Отделение корней
Этап отделения корней основан на теореме Коши: если функция на концах отрезка имеет разные знаки, то на этом отрезке содержится, по крайней мере, один корень.
Корень ξ уравнения f(x)=0считается отделенным (локализованным) на отрезке [α;β] , если на этом отрезке данное уравнение не имеет других корней. Чтобы отделить корни уравнения, необходимо разбить область допустимых значений функции f(x) на отрезки, в каждом из которых содержится только один корень. Существуют графический и аналитический способы отделения корней.
9
2.2.1. Графическое отделение корней
Графическое отделение корней основано на графическом способе решения уравнений – отыскании точек, в которых функция f(x)пересекает ось 0Х.
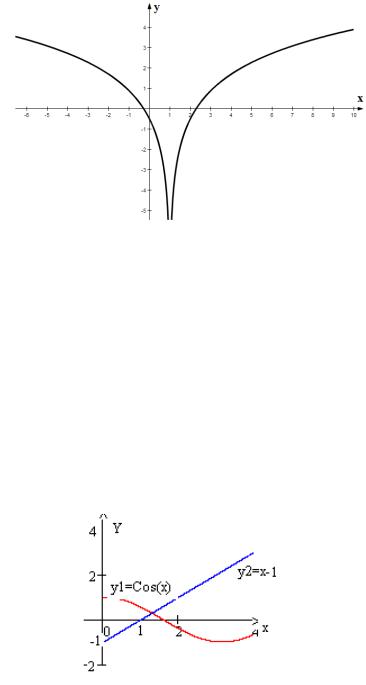
Пример 2.2-1.Отделить корни уравнения ln (x-1)2 – 0.5 = 0.
На рис. 2.2-1 изображен график функции y = ln (x-1)2 – 0.5, из которого следует, что уравнение имеет два действительных корня ξ1 [-1;0] и ξ2 [2;3].
Рис.2.2-1
В некоторых случаях удобно вначале представить функцию f(x) в виде f(x)=g1(x) - g2(x), из которого, при условии f(x)=0, следует, что g1(x)=g2(x).
Абсциссы точек пересечения графиков y1=g1(x)и y2=g2(x) являются значениями корней уравнения.
Пример 2.2-2. Отделить корни уравнения сos(x) – x + 1 = 0.
Приведем исходное уравнение к виду сos(x) = x – 1. Построив графики функций y1 = сos(x) и y2 = х – 1 (рис. 2.2-2), выделим отрезок, содержащий
корень
ξ
[1;2].
Рис. 2.2-2
10
