f (x)
где
при
m1и M1
x [a, b]
– соответственно, наименьшее и наибольшее значения
.
В случае, если M1<2m1, то для оценки погрешности метода может быть использована формула
| xn-xn-1| .
2.2.Алгоритмы методов интерполяции функции
2.2.1. Метод Лагранжа
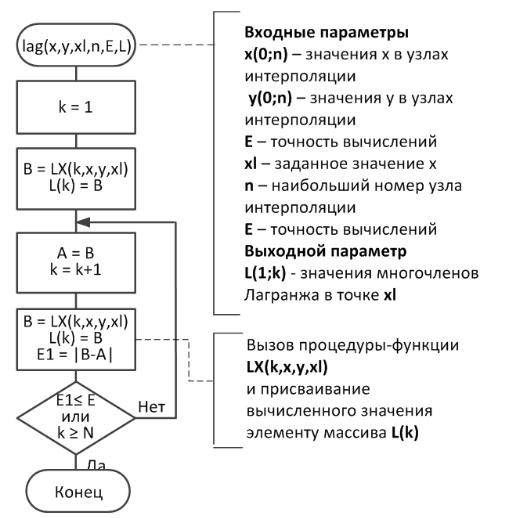
Схемы алгоритмов, используемые при вычислении значения функции по формуле Лагранжа, представлены на рис.2.2-1 и 2.2-2.
Рис.2.2-1. Алгоритм интерполяции функции с заданной точностью
18
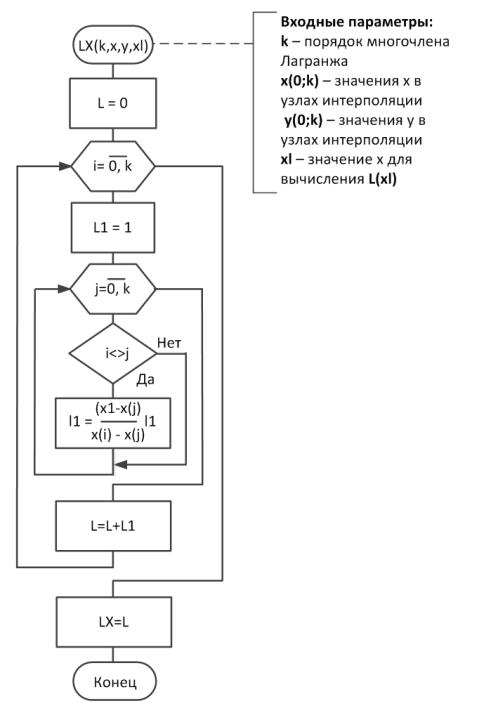
Рис.2.2-2. Алгоритм интерполяции функции с заданным количеством узлов
При интерполяции по методу Лагранжа функция f(x) может быть задана в (n+1)узлах, произвольно расположенных на отрезке [a;b]: y0 = f(x0), y1 = f(x1), … yn = f(xn).
Общий вид интерполяционной формулы[3]
n |
(x x0 )(x x1)...(x i 1)(x xi 1)...(x xn ) |
|
|
||||||||||||||||
Ln (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi |
(x |
|
x |
|
)(x |
|
x )...(x |
|
x |
|
)(x |
|
|
)...(x |
|
x |
|
) |
||
i 0 |
i |
0 |
i |
i |
i 1 |
i |
i |
n |
|
||||||||||
|
|
|
1 |
|
|
i 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|