
Временные диаграммы



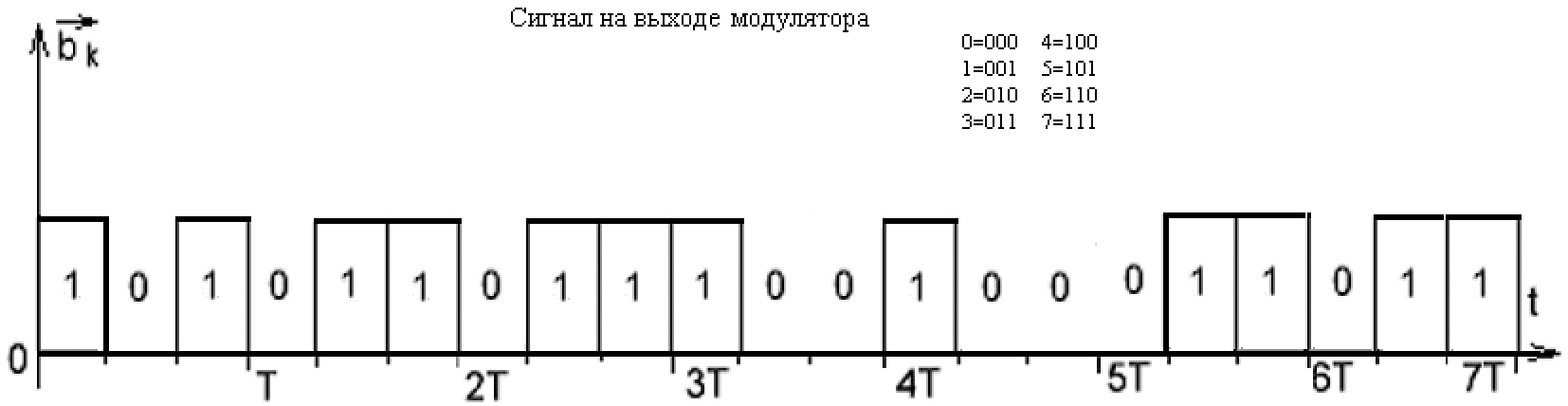
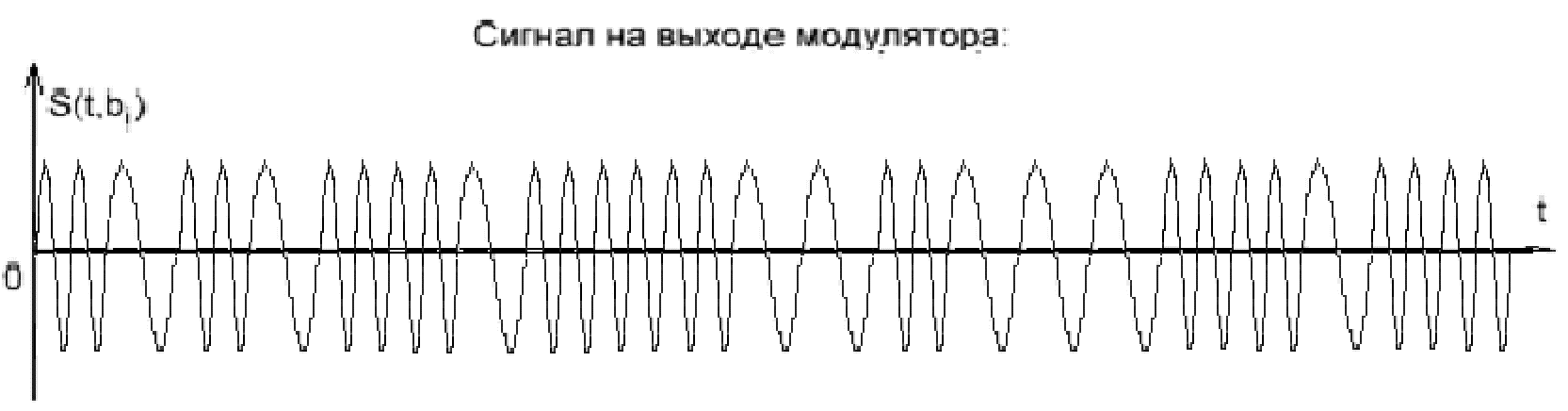




Выполнение задания
2. По заданной функции корреляции исходного сообщения:
2. а) Рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра
2. б) Построить в масштабе графики функции корреляции и спектра плотности мощности, отметив на них найденные в 2. а) параметры
Найдем интервал корреляции:

Это плотность мощности сообщения.
Построим энергетический спектр. т.е. спектр плотности мощности сообщения:

Рисунок 2 – График энергетического спектра
Графически найдем максимальное значение энергетического спектра:

Спектр плотности мощности сообщения:

Рисунок 3 – График спектра мощности
Функция корреляции сообщения:
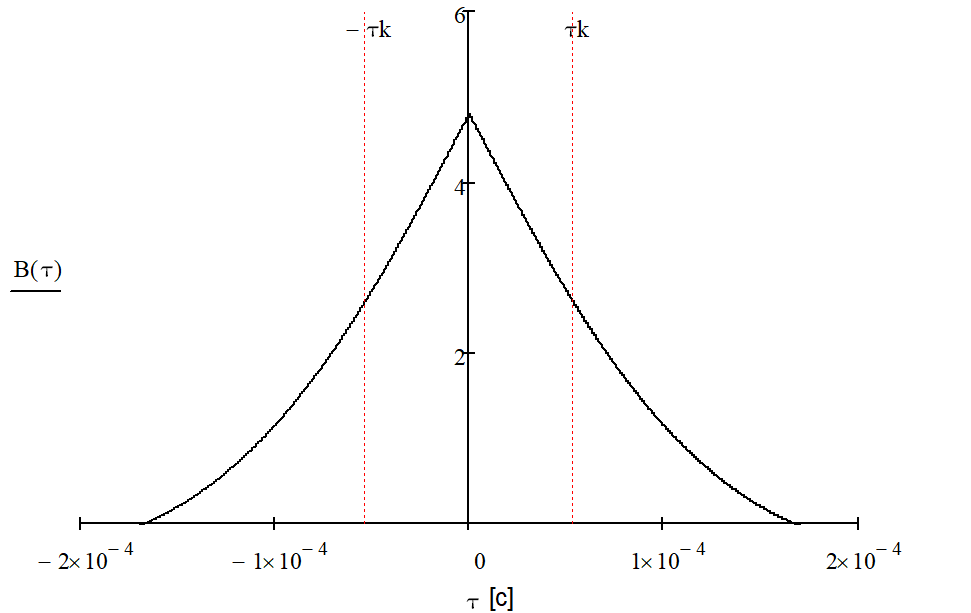
Рисунок 4 – График функции корреляции
3. Исходное сообщение воздействует на идеальный фильтр нижних частот с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения.
3. а) Рассчитать среднюю квадратичную погрешность фильтрации (СКПФ) сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ.
Средняя квадратическая погрешность фильтрации

Найдем среднюю мощность отклика ИФНЧ:

Рассчитаем частоту и интервал временной дискретизации отклика ИФНЧ:
![]()
![]()
Интервал временной дискретизации

4. Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования, найти:
4. а) интервал квантования, пороги и уровни квантования, среднюю квадратическую погрешность квантования (СКПК)
![]()
Пороги квантования:
![]()
Таблица 2 – Значения порогов квантования
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
h(n), B |
-5.642 |
-3.762 |
-1.881 |
0 |
1.881 |
3.762 |
5.642 |
Уровни квантовани:
![]()
Таблица 3 – Значения уровней квантования
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
x(n), B |
-6.583 |
-4.702 |
-2.821 |
-0.94 |
0.94 |
2.821 |
4.702 |
6.583 |
Вычислим среднеквадратическую погрешность квантования:

Таблица 4 – Значения ФПВ для различных значений порогового квантования
h(n), B |
-5.642 |
-3.762 |
-1.881 |
0 |
1.881 |
3.762 |
5.642 |
|
0.00236 |
0.02871 |
0.12866 |
0.21212 |
0.12866 |
0.02871 |
0.00236 |

Таблица 5 - Таблица значений для расчета выходного сигнала квантователя
|
43.331 |
22.108 |
7.959 |
0.884 |
0.884 |
7.959 |
22.108 |
43.331 |
p(n) |
0.00132 |
0.0214 |
0.1359 |
0.34134 |
0.34134 |
0.1359 |
0.0214 |
0.00132 |
4. Построим характеристику квантования:
Характеристика квантования:
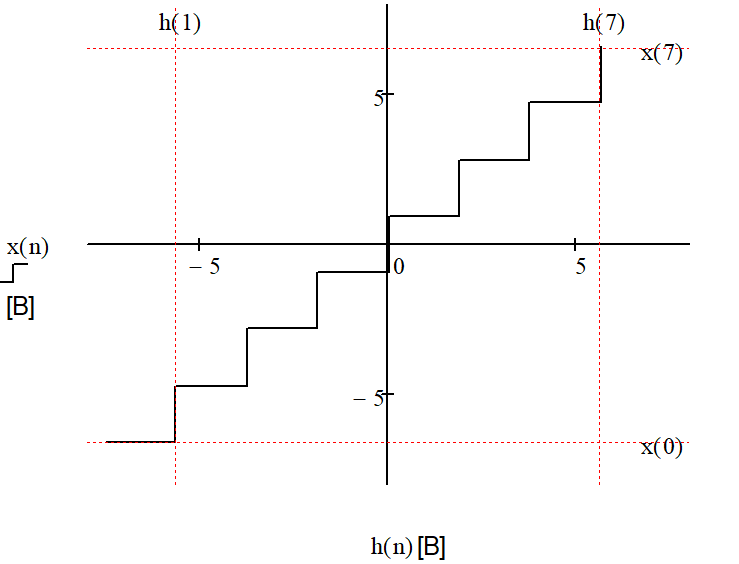
Рисунок 5 – График характеристики квантования
5.а) Рассмотрим отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи.
5.б) Рассчитать закон и функцию распределения вероятности квантованного сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника.

Производительность или скорость ввода информации в ДКС определяется соотношением:

5.б) Построить в масштабе графики рассчитанных законах и функции распределений вероятностей:

Рисунок 6 – График закона распределения вероятности

Таблица 6 – Значения функции распределения вероятностей квантового сигнала
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
f(n) |
0.0013 |
0.0227 |
0.1586 |
0.5 |
0.8413 |
0.9772 |
0.9986 |
1 |

Рисунок 7 – График функции распределения вероятности
6. Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний:
Таблица 7 – Результат кодирования дискретного сигнала
|
0 |
000 |
|
1 |
001 |
|
2 |
010 |
|
3 |
011 |
|
4 |
100 |
|
5 |
101 |
|
6 |
110 |
|
7 |
111 |
Таблица 8 – Таблица кодовых расстояний
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
000 |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
001 |
1 |
0 |
2 |
1 |
2 |
1 |
3 |
2 |
010 |
1 |
2 |
0 |
1 |
2 |
3 |
1 |
2 |
011 |
2 |
1 |
1 |
0 |
3 |
2 |
2 |
1 |
100 |
1 |
2 |
2 |
3 |
0 |
1 |
1 |
2 |
101 |
2 |
1 |
3 |
2 |
1 |
0 |
2 |
1 |
110 |
2 |
3 |
1 |
2 |
1 |
2 |
0 |
1 |
111 |
3 |
2 |
2 |
1 |
2 |
1 |
1 |
0 |
6.а) Рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ.
Так как среднее число нулей и единиц в сигнале ИКМ одинаково (это справедливо для гауссовского сообщения и данного способа кодирования), то и вероятности их появления одинаковы: P0=0.5; P1=0.5
Найдем начальную ширину спектра сигнала ИКМ:

7. Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС)
Используется гармонический переносчик:
а) Рассчитать нормированный к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра.
б) Построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра.
Двоичные кодовые символы сигнала ИКМ передаются с помощью ДЧМ.


Таблица 9 – Значения нормированного спектра сигнала дискретной модуляции


Рисунок 8 – График нормированного спектра сигнала дискретной модуляции
8. Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот,
равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:
8.а) Рассчитать приходящий в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи

Пропускная способность НКС характеризует максимально возможную скорость передачи информации по данному каналу
![]()
8.б) Построим в масштабе 4 графика ФПВ мгновенных значений и огибающей УГП и суммы УГП и гармонического сигнала
УГП-узкополосная гуассовская помеха

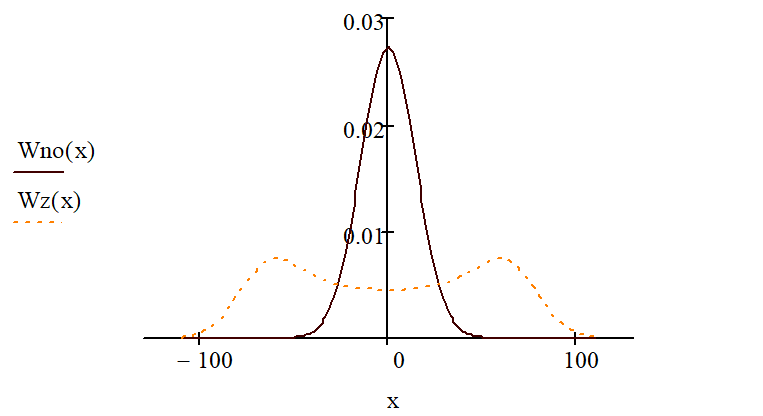
Рисунок 9 – График ФПВ мгновенных значений УГП и суммы гармонического сигнала с УГП


Рисунок 10 – График огибающей гауссовской помехи и огибающей суммы гармонического сигнала с УГП
9. С учетом заданного вида приема сигнала дискретной модуляции:
9. а) Рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС:

9.б) Изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы. Пояснить случаи, когда он выносит ошибочные решения.

Рисунок 11 – Схема приемника сигналов дискретной модуляции
Частотный детектор, представляющий собой нелинейный преобразователь и ФНЧ, выделяет огибающую принимаемого сигнала ДЧМ, прошедшего полосовой фильтр с эффективной полосой пропускания, равной ∆fsдчм. К дискретизатору проводятся отклик детектора U(t) и последовательность дискретизирующих импульсов δτи (t) с периодом τи, которые необходимы для взятия отсчета в середине посылки длительностью τи. В РУ (решающем устройстве) отсчеты Uk сравниваются с пороговым напряжением α_0и принимается решение – передана 1, если Uk≥α0, или передан 0, если Uk<α0. Под действием помех в канале связи частота сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0.
10. Рассматривая отклика декодера ПРУ как случайный дискретный сигнал на выходе L-ичного ДКС
10.а) Рассчитать распределение вероятностей дискретного сигнала на выходе детектора, скорость передачи информации по L-ичному ДКС, относительные потери в скорости передачи информации по L-ичному ДКС
10.б) Построить в масштабе график закона распределения вероятностей отклика декодера

Графики закона распределения вероятностей отклика декодера и закона распределения вероятностей отклика квантователя совпадают:
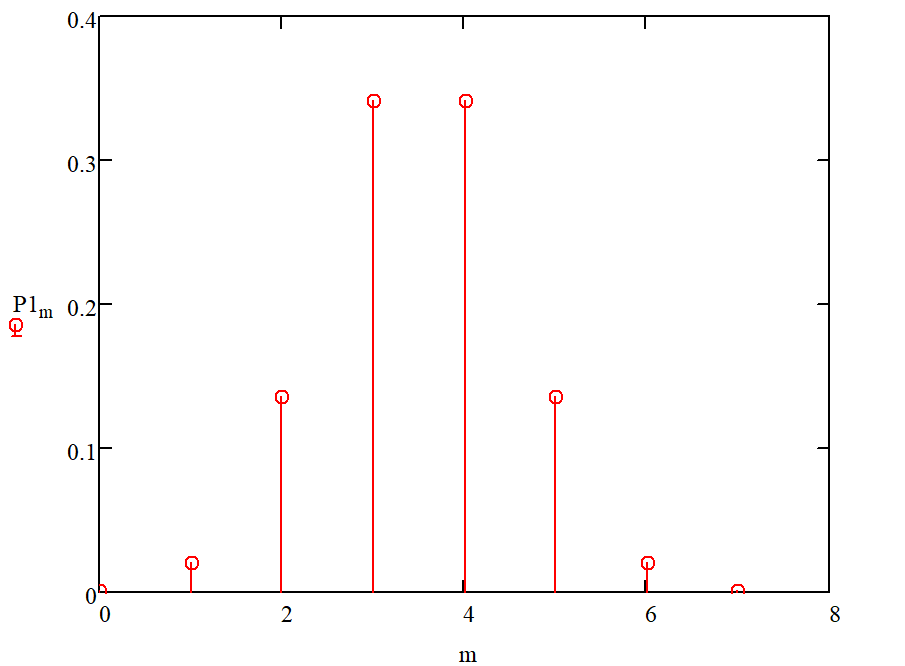
Рисунок 12 - Закона распределения вероятностей отклика декодера
Рисунок 13 – График закона распределения вероятности

11. Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:
11.а) Рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПК), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП)



 ,
,








