
Slinkina_Mekh_i_mol_fiz_2
.pdf
|
m |
|
i |
RdT + pdV |
|
|
|
|
|
|
|
|
|
|
|
= m |
|
i |
T |
dT |
V |
mRdV |
|
||
|
µ 2 |
|
|
|
||||||||
1) ∆S1 = ∫ |
|
|
R ∫2 |
+ ∫2 |
= |
|||||||
|
|
|
T |
|
T |
µV |
||||||
|
|
|
|
µ |
2 |
T |
V |
|
||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
=m i R ln T2 + m R ln V2 .
µ2 T1 µ V1
V2 ,
V1
Отношение |
|
T2 |
|
при изобарическом процессе равно отношению |
||||||||||||||||
|
T |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆S |
|
m |
|
i |
R ln |
V |
|
m |
R ln |
V |
|
m |
R ln |
V |
i |
|
|
|||
= |
µ |
|
|
|
2 |
+ |
µ |
2 |
= |
µ |
2 |
|
|
+1 |
= |
|||||
2 |
|
|
||||||||||||||||||
1 |
|
|
|
|
|
V |
|
|
V |
|
|
V |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
= |
|
2 10−3 |
8,31 ln3 |
3,5 |
=3,1 |
Дж |
; |
|
|
|
||||
|
|
|
|
|
|
2 10−3 |
|
|
Кo |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
∆S2 |
|
pdV |
V2 |
mRdV |
|
m |
R ln |
V |
|
|
2 10−3 8,31 ln 3 |
|
Дж |
|
|||
2) |
= ∫ |
|
= ∫ |
|
|
= |
|
2 |
= |
|
|
|
=9,2 |
|
. |
|||
T |
|
µV |
µ |
|
2 10−3 |
Кo |
||||||||||||
|
|
|
V |
|
|
|
V |
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
96
5 . РЕАЛЬНЫЕ ГАЗЫ. ЖИДКОСТИ
Основные формулы
1. Уравнение Ван-дер-Ваальса для одного моля газа
(p +a /Vm2 )(Vm −b)= RT,
для произвольного количества вещества ν газа
(p +ν2a /V 2 )(V +νb)= νRT,
где a и b – постоянные Ван-дер-Ваальса (рассчитанные на один моль газа); V – объем, занимаемый газом; Vm – молярный объем;
р – давление газа на стенки сосуда;
p′ = |
a |
, или |
p′ = |
ν2a |
– внутренне давление, обусловленное сила- |
V 2 |
V 2 |
||||
|
m |
|
|
|
|
ми взаимодействия молекул.
2. Связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:
Vm кр =3b, pкр = a /(27b2 ), Tкр =8a(27Rb).
3. Внутренняя энергия реального газа
U = ν(CV T −a /Vm ),
где СV – молярная теплоемкость газа при постоянном объеме. 4. Поверхностное натяжение
σ = F / l,
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости, или
σ = ∆E / ∆S,
где ∆Е – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади ∆S поверхности этой пленки.
5. Формула Лапласа в общем случае записывается в виде
|
1 |
|
1 |
|
|
|
+ |
|
|||
R |
R |
||||
p = σ |
, |
||||
|
1 |
|
2 |
|
|
|
97 |
|
|
|

где р – давление, создаваемое изогнутой поверхностью жидкости; σ – поверхностное натяжение;
R1 и R2 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости, а в случае сферической поверхности
p= 2σ/ R.
6.Высота подъема жидкости в капиллярной трубке
h = 2σcos θ/(ρgR),
где θ – краевой угол;
R – радиус канала трубки; ρ – плотность жидкости;
g– ускорение свободного падения.
7.Высота подъема жидкости между двумя близкими и параллельными плоскостями
h = 2σcos θ/(ρgh),
где d – расстояние между плоскостями.
8. Расход жидкости в трубке тока: а) объемный расход QV = vS;
б) массовый расход Qm = ρvS, где S – площадь поперечного сечения трубки тока; v – скорость жидкости; ρ – ее плотность.
9. Уравнение неразрывности струи
v1S1 = v2S2 ,
где S1 и S2 – площади попереч-
ного сечения трубки тока в двух
местах;
v1 и v2 – соответствующие














 скорости течений.
скорости течений.
10. Уравнение Бернулли для идеальной несжимаемой жидкости в общем случае
p1 +ρv12 / 2 +ρgh1 = p2 +ρV22 / 2 +ρgh2 ,
где р1 и р2 – статические давления жидкости в двух сечениях трубки тока; v1 и v2 – скорости жидкости в этих сечениях;
ρv12 / 2 и ρv22 / 2 – динамические давления жидкости в этих же сечениях;
98

h1 и h2 – высоты сечений над некоторым уровнем; ρgh1 и ρgh2 – гидростатические давления.
Уравнения Бернулли в случае, когда оба сечения находятся на одной высоте (h1 = h2),
p1 +ρv12 / 2 = p2 +ρv22 / 2.
11. Скорость течения жидкости из малого отверстия в открытом широком сосуде
v = 2gh,
где h – глубина, на которой находится отверстие относительно уровня жидкости в сосуде.
Примеры решения задач
Задача 1 . Бак, имеющий форму куба, длина ребра которого l, наполнен водой. Определить силу давления на стенку бака со стороны воды, если атмосферное давление равно р0.
Дано: Решение
l, ρ, p0
F = ?
На рисунке показан график зависимости давления от глубины погружения h. Давление на боковую стенку линейно зависит от h, следовательно,
F = pср S = p1 +2 p2 l2 ,
где р1 = р0; р2 = р0 + ρgl.
Таким образом, F = p0 + 1 ρgl l2.
2
Ясно, что сила давления не будет приложена в центре грани куба, а будет несколько смещена вниз.
99
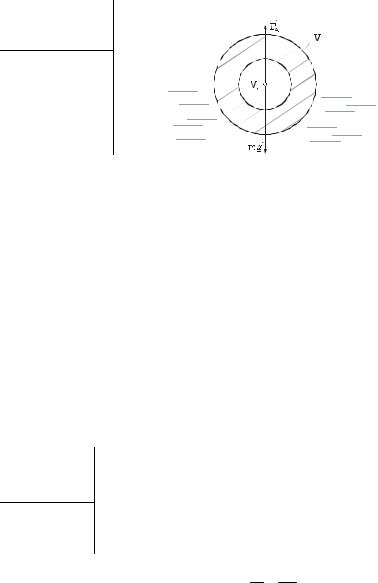
Задача 2 . Полный медный шар, наружный объем которого V, плавает в воде так, что половина его погружена в воду. Найти объем полости шара, если плотность меди ρ1, а воды – ρ2.
Дано: Решение
ρ1; ρ2; V
V0 = ?
Так как шар находится в равновесии, то FA = mg.
Масса шара m = ρ1 (V – V0).
По закону Архимеда FA = 12 ρ2 gV.
Получим уравнение
12 ρ2V g = ρ1g(V −V0 ),
откуда
|
|
|
1 |
|
ρ2 |
|
V0 |
|
− |
|
|
||
=V 1 |
2 |
ρ |
. |
|||
|
|
|
|
|
1 |
|
Задача 3 . Найти добавочное давление, обусловленное поверхностным натяжением, внутри шаровой капли радиусом R. Коэффициент поверхностного натяжения жидкости равен σ.
Дано:
σ; R
∆р = ?
Решение
Рассечем мысленно каплю диаметральной плоскостью на две половинки. Вследствие поверхностного натяжения обе половинки притягиваются друг к другу с силой F = σl = σ 2πR. Эта сила прижимает друг к другу оба полушария по поверхности S = πR2, поэтому
∆p = FS = 2Rσ.
100

Задача 4 . Найти массу воды, поднявшейся по стеклянной капиллярной трубке диаметром 0,5 мм, если коэффициент поверхностного натяжения воды 7,2 ·10–2 Н/м.
Дано:
σ = 7,2 ·10–2 Н/м d = 0,5 ·10–3 м
т = ?
Решение
Сила поверхностного натяжения, действующая по краю мениска жидкости, направлена вверх и уравновешивает силу тяжести столбика жидкости.
2πRσ = mg, σπd = mg,
откуда
m = πdgσ =1,2 10−5 кг.
Задача 5 . Из трубы сечением S1 бьет вертикально вверх струя воды. Найти сечение струи на высоте h над отверстием трубы. Расход воды из трубы равен Q.
Дано: |
|
Решение |
|||
S1; h; Q |
Уравнение Бернулли для данного случая: |
||||
|
|
v2 |
v2 |
||
S2 = ? |
|
||||
|
ρ |
1 |
=ρ |
2 |
+ρgh, |
|
2 |
2 |
|||
|
|
|
|
||
где v1 – скорость воды в сечении S1;
v2 – скорость в сечении струи S2 на высоте h. Уравнение неразрывности
S1v1 = S2 v2 = Q.
Отсюда находим v1 и v2 и подставляем в уравнение Бернулли:
Q2 = Q2 + 2gh,
S12 S22
откуда
S2 = |
Q S1 |
. |
|
Q2 −2ghS 2 |
|||
|
|
||
|
1 |
|
101
КОНТРОЛЬНАЯ РАБОТА № 2
Студент-заочник должен решить семь задач того варианта, номер которого совпадает с третьей цифрой справа его шифра.
Пример. Номер шифра (номер зачетной книжки) 13799. Студент решает седьмой вариант.
Вариант |
|
|
Номера задач |
|
|
||
0 |
3 |
15 |
21 |
34 |
42 |
53 |
62 |
1 |
7 |
12 |
27 |
40 |
44 |
58 |
65 |
2 |
5 |
19 |
30 |
33 |
48 |
51 |
67 |
3 |
10 |
16 |
22 |
35 |
46 |
59 |
61 |
4 |
6 |
11 |
26 |
38 |
43 |
54 |
64 |
5 |
8 |
20 |
29 |
31 |
49 |
56 |
68 |
6 |
1 |
14 |
23 |
36 |
47 |
60 |
69 |
7 |
9 |
17 |
25 |
37 |
45 |
52 |
63 |
8 |
4 |
13 |
24 |
32 |
50 |
57 |
66 |
9 |
2 |
18 |
28 |
39 |
41 |
55 |
70 |
1.Открытую стеклянную трубку длиной l = 1 м наполовину погружают в ртуть. Затем трубку закрывают пальцем и вынимают. Какой длины останется в трубке столбик ртути? Атмосферное давление равно 750 мм рт. ст.
2.Посередине откачанной и запаянной с обоих концов горизонтальной трубки длиной L = 1 м находится столбик ртути высотой h = 20 см. Если трубку поставить вертикально, столбик ртути сместится на l = 10 см. До
какого давления была откачана трубка? Плотность ртути ρ = 1,36 ·104 кг/м3.
3.Два баллона соединены трубкой с краном. В первом находится газ при давлении 105 Па, во втором – при давлении 0,6 ·105 Па. Объем первого баллона V1 = 1 л, второго – V2 = 3 л. Какое давление установится
вбаллонах, если открыть кран? Температура постоянная. Объемом трубки можно пренебречь.
4.Три баллона емкостью V1 = 3 л, V2 = 7 л и V3 = 5 л наполнены соответственно кислородом (р1 = 2 ·105 Па), азотом (р2 = 3 ·105 Па) и углекислым газом (р3 = 0,6 ·105 Па) при одной и той же температуре. Баллоны соединяют между собой, причем образуется смесь той же температуры. Каково давление смеси?
102
5. Дан график изменения состояния идеального газа в координатах р, V. Представить этот цикл в координатах р, T и V, Т.
p
1 
 2
2
4 
 3
3
 V
V
6. В цилиндре, площадь основания которого равна S = 100 см2, находится воздух при температуре 12 °С. Атмосферное давление 105 Па. На высоте h = 60 см от основания цилиндра расположен поршень. На сколько опустится поршень, если на него поставить гирю массой т = 100 кг, а воздух в цилиндре при этом нагреть до 27 °С? Трение поршня о стенки цилиндра и вес самого поршня не учитывать.
7.Из баллона со сжатым водородом емкостью V = 10 л вследствие
неисправности вентиля утекает газ. При температуре t1 = 7 °С манометр показывал р = 5 ·106 Па. Через некоторое время при температуре t2 = 17 °С манометр показал такое же давление. Сколько утекло газа?
8.Сколько молекул воздуха выходит из комнаты объемом V0 = 120 м3 при повышении температуры от t1 = 15 °С до t2 = 25 °С? Атмосферное давление р0 = 105 Па.
9.При какой температуре кислород (О2), находясь под давлением 0,2 ·106 па, имеет плотность 1,2 кг/м3?
10.В сосуде при температуре t = 100 °С и давлении р = 4 ·105 Па находится 2 м3 смеси кислорода О2 и сернистого газа SO2. Определить парциальное давление компонентов, если масса сернистого газа 8 кг.
11.В баллоне емкостью 0,05 м3 находятся 0,12 кмоль газа при давлении 0,6 ·107 Па. Определить среднюю кинетическую энергию теплового движения молекул газа.
12.Найти средние квадратичные скорости молекул азота и кислорода при температуре 27 °С.
13.Найти импульс молекулы водорода при температуре 20 °С. Скорость молекулы считать равной средней квадратичной скорости.
14.В сосуде объемом 5 л находится 20 г кислорода под давлением 105 Па. Найти: 1) среднюю квадратичную скорость молекул газа; 2) число молекул, находящихся в сосуде; 3) плотность газа.
15.Средняя квадратичная скорость молекул некоторого газа равна 500 м/с. Давление газа равно 5 ·104 Па. Найти плотность газа при этих условиях.
16.Средняя квадратичная скорость молекул некоторого газа при нормальных условиях равна 461 м/с. Какое количество молекул содержится в 1 г этого газа?
103
17.Чему равна энергия вращательного движения молекул, содержащихся в 1 кг азота при температуре 7 °С?
18.Чему равна энергия теплового движения молекул двухатомного
газа, заключенного в сосуд объемом 2 л и находящегося под давлением в
1,5 ·105 Па?
19.1 кг двухатомного газа находится под давлением 8·104 Па и имеет плотность 4 кг/м3. Найти энергию теплового движения молекул газа при этих условиях.
20.Какое число молекул двухатомного газазанимаетобъем V = 10 см3 при давлении 40 мм рт. ст. и при температуре 27 °С? Какой энергией теплового движения обладают эти молекулы?
21.Кинетическая энергия поступательного движения молекул азота, находящегося в баллоне объемом 0,02 м3, равна 5 ·103 Дж, а средняя квадратичная скорость его молекул равна 2 ·103 м/с. Найти: 1) количество азота в баллоне; 2) давление, под которым находится азот.
22.Смесь состоит из двух молей одноатомного газа и одного моля
двухатомного газа. Определить мольные теплоемкости CµV и Cµ p смеси.
23.Вычислить теплоемкость при постоянном объеме двухатомного газа, заключенного в сосуд V = 10 л при нормальных условиях.
24.Разность удельных теплоемкостей некоторого двухатомного га-
за ср – сV = 2,08 кДж/кг ·К. Определить молярную массу µ газа и его удельные теплоемкости ср и сV.
25.Каковы удельные теплоемкости ср и сV смеси газов, содержащей кислород массой т1 = 10 г и азот массой т2 = 20 г?
26.Определить удельную теплоемкость сV смеси газов, содержащей V1 = 5 л водорода и V2 = 3 л гелия. Газы находятся при одинаковых условиях.
27.В баллоне находятся аргон и азот. Определить удельную тепло-
емкость сV смеси газов, если массовые доли аргона и азота одинаковы и равны 0,5.
28.Вычислить удельные теплоемкости ср и сV газов: 1) гелия; 2) углекислого газа.
29.Для некоторого двухатомного газа удельная теплоемкость при постоянном давлении равна 840 Дж/кг· К. Чему равна масса одного моля этого газа?
30.Чему равны удельные теплоемкости ср и сV некоторого двухатомного газа, если плотность этого газа при нормальных условиях равна
1,43 кг/м3?
104
31.Найти среднюю длину свободного пробега молекул азота при температуре 17 °С и давлении 104 Па.
32.Найти среднюю длину свободного пробега атомов гелия в условиях, когда плотность гелия 2,1 ·10–2 кг/м3.
33.Найти среднее число столкновений в 1 с молекул азота при t = 27 °С и давлении р = 0,5 ·105 Па.
34.Найти среднюю длину свободного пробега молекул воздуха
при нормальных условиях. Диаметр молекул воздуха условно принять равным 3 ·10–10 м.
35.В колбе объемом 100 см3 находится 0,5 г азота. Найти среднюю длину свободного пробега молекул азота при этих условиях.
36.Найти коэффициент внутреннего трения азота при нормальных
условиях, если коэффициент диффузии для него при этих условиях равен
0,142 см2/с.
37.Найти диаметр молекулы кислорода, если известно, что для кислорода коэффициент внутреннего трения при 0 °С равен 18,8 ·10–6 Н·с/м2?
38.Найти коэффициент диффузии и коэффициент внутреннего
трения воздуха при давлении 105 Па и температуре 10 °С. Диаметр молекулы воздуха принять равным 3 ·10–10 м.
39.Найти коэффициент диффузии гелия при нормальных условиях.
40.Какая часть молекул водорода при температуре 0 °С обладает скоростями от 2000 м/с до 2100 м/с.
41.Один киломоль воздуха при давлении р1 = 106 Па и температуре Т1 = 390 °К изохорически изменяет давление так, что его внутренняя энергия изменяется на ∆U = –71,7 кДж, затем изобарически расширяется
исовершает работу А = 745 кДж. Определить параметры воздуха (считать
сV = 721 Дж/кг ·К = const).
42.При изобарическом сжатии азота была совершена работа, равная 12 кДж. Определить затраченное количество теплоты и изменение внутренней энергии газа.
43.Определить работу расширения 7 кг водорода при постоянном давлении и количество теплоты, переданное водороду, если в процессе
нагревания температура газа повысилась на 200 °С.
44. В цилиндре диаметром 20 см и высотой 42 см с подвижным поршнем находится газ под давлением 12 ·105 Па при температуре 300 °С. Определить работу, совершаемую газом при снижении температуры до 10 °С при постоянном давлении.
105
