Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский государственный университет науки и технологий им. академика М.Ф. Решетнева

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Slinkina_Mekh_i_mol_fiz_2

.pdf

Скачиваний:

Добавлен:

17.03.2015

Размер:

1.07 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

7. Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле

A = ∫ pdV ,

где V1 – начальный объем газа;

V2 – его конечный объем.

Работа газа при изобарическом процессе (р = const):

A = p (V2 −V1 );

при изотермическом процессе (Т = const):

A = (m / µ)RT ln (V2 /V1 );

при адиабатическом процессе:

RT1

v−1

A =

CV (T1 −T2 ) или

A =

− V

γ −1

где Т1 – начальная температура газа; Т2 – его конечная температура.

8. Уравнение Пуассона (уравнение газового состояния при адиабатическом процессе)

pV γ = const.

9. Связь между начальным и конечным значениями параметров состояний газа при адиабатическом процессе:

γ−1

(γ−1)/ γ

;

= V

10. Первое начало термодинамики в общем случае записывается в

виде

Q = ∆U + A,

где Q – количество теплоты, сообщенное газу;

∆U – изменение его внутренней энергии;

A – работа, совершаемая газом против внешних сил.

Первое начало термодинамики при изобарическом процессе:

Q = ∆U + A = mµ CV ∆T + mµ R∆T = mµ Cp∆T;

при изохорическом процессе (А = 0):

Q = ∆U = (m / µ)CV ∆T;

при адиабатическом процессе (Q = 0):

A= −∆U = −(m / µ)CV ∆T.

11.Термический коэффициент полезного действия (КПД) цикла в общем случае

η= (Q1 −Q2 )/ Q1 ,

где Q1 – количество теплоты, полученное рабочим телом (газом) от нагревателя;

Q2 – количество теплоты, переданное рабочим телом охладителю. КПД цикла Карно

η= (Q1 −Q2 )/ Q1; или η= (T1 −T2 )/ T1 ,

где Т1 – температура нагревателя; Т2 – температура охладителя.

12. Изменение энтропии

B	dQ	,
∆S = ∫	T	,
A	T

где А и В – пределы интегрирования, соответствующие начальному и конечному состояниям системы.

Так как процесс равновесный, то интегрирование проводится по любому пути.

13. Формула Больцмана

S = k ln W ,

где S – энтропия системы;

W – термодинамическая вероятность ее состояния; k – постоянная Больцмана.

Примеры решения задач

Задача 1 . В вертикальном цилиндре под тяжелым поршнем находится кислород массой т = 1 кг. Для повышения температуры кислорода на ∆Т = 10 °К ему было сообщено количество теплоты Q = 9,1 кДж. Найти удельную теплоемкость кислорода, работу, совершаемую им при расширении, и увеличение его внутренней энергии.

Дано:

m = 1 кг

µ = 32 ·10–3 кг/моль Q = 9,1·103 Дж

∆Т = 10 °К

cр = ? А = ?

∆U = ?

Решение

Так как поршень в любой момент находится в равновесии, то во время нагревания кислорода его давление р остается также постоянным. Тогда удельная теплоемкость при постоянном давлении

cp =	Q	= 910	Дж	.
	m ∆T
			кг К

Работа расширения при постоянном давлении

A = p (V2 −V1 ),

где V1 и V2 – начальный и конечный объем газа. Уравнение состояния газа до и после нагревания

pV = m RT			(1)
1	µ	1
и
pV = m RT .			(2)
2	µ	2
Вычитая из выражения (2) выражение (1), найдем
p (V −V )	= mR (T −T ),
2 1	µ	2	1

следовательно,

A = mµ R ∆T = 2,6 кДж.

Подводимое к газу количество теплоты идет на увеличение его внутренней энергии ∆U и на совершение работы А:

Q = ∆U + A,

отсюда

∆U = Q − A = 6,5 кДж.

Задача 2 . В цилиндре с площадью основания 100 см2 находится воздух при температуре 17° С. На высоте 50 см от основания цилиндра расположен легкий поршень, на котором лежит гиря весом 50 кГ. Какую работу совершит газ при расширении, если его нагреть на 50 °С? Атмосферное давление 760 мм рт. ст.

Дано:

S = 100 см2 = 0,01 м2

Т1 = 290 °К h = 0,5 м

Р0 = 150 кГ = 1470 Н рА = 760 мм рт. ст. = 1·105 Па ∆Т = 50 °К

А = ?

Решение

В процессе нагревания газ расширяется и совершает работу по преодолению веса груза и силы атмосферного давления, действующих на поршень. Так как эти силы постоянны, то при достаточно медленном нагревании газ будет расширятся изобарически и его работу можно вычислить:

A = p (V2 −V1 ).

При равновесии поршня давление р уравновешивается атмосферным давлением рА и давлением, создаваемым гирей весом Р0:

p = pA +

По закону Гей-Люссака

= V2

или

= V2

следовательно,

hS (T

−T )

= 2,1 102

A = pA +

Дж.

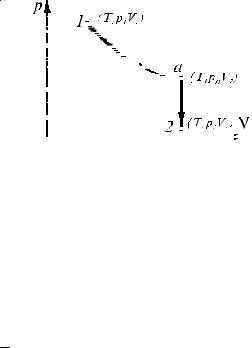
Задача 3 . Азот, занимавший при давлении р1 = 2 ·105 Па объем V1 = 5 л, расширяют до объема 8 л, при этом давление падает до значения р2 = 105 Па. Процесс происходит сначала по изотерме, затем – по изохоре. Определить работу сил давления газа, изменение внутренней энергии и количество поглощенной теплоты при этом переходе.

Дано:

Решение

= 2·105 Па

= 5

л = 5·10–3 м3

= 8

л = 8·10–3 м3

µ = 28·10–3 кг/моль

р2

= 105 Па

i = 5

Q12 = ? ∆U12 = ?

А12 = ?

При переходе из состояния 1 в состояние 2 надо рассмотреть каждый из указанных процессов отдельно, тогда

A12 = A1a + Aa2 ; Q12 = Q1a +Qa2 .

(1)

Изменение внутренней энергии не зависит от процесса и в любом

случае

∆U	12	=	i		m	R (T −T ).		(2)

		2		µ		2	1

Используя уравнение Менделеева–Клапейрона для состояний 1 и 2, получим

∆U = 2i (p2V2 − p1V1 )= −500 Дж.

Работа газа при изотермическом расширении

A	=	m	RT	ln	V2	= p V	ln	V2	= 470 Дж.
					V			V
1a	µ 1					1 1
					1			1

Учитывая, что Аа 2 = 0, находим А12 = А1а = 470 Дж. Для изотермического процесса (участок 1–а)

Q1a = A1a = 470 Дж; ∆U1a = 0 .

Для изохорического процесса (участок а–2)

Qa2 = ∆Ua2 = ∆U12 = −500 Дж.

Общее количество теплоты

Q12 = Q1a +Qa2 = 470 +(−500)= −30 Дж.

Знак минус показывает, что газ отдавал теплоту окружающим телам.

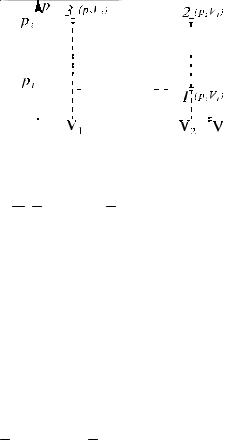
Задача 4 . Некоторая масса азота при давлении 1 атм имела объем 5 л, а при давлении 3 атм – объем 2 л. Переход от начального к конечному состоянию был сделан в два этапа: сначала по изохоре, а затем по изобаре. Определить изменение внутренней энергии, количество теплоты и произведенную работу.

Дано:

Решение

i = 5

Покажем графически, как происходил пере-

р1 = 1 атм = 105 Па

ход газа от первого состояния ко второму:

V1 = 5 л = 5·10–3 м3

р2 = 3 атм = 3·105 Па

V2 = 2 л = 2·10–3 м3

µ = 32·10–3 кг/моль

∆U = ?

Q = ?

A = ?

1) При изохорном процессе вся теплота идет только на изменение внутренней энергии, работа при изохорном процессе не совершается, т. е.

Q1−2 = ∆U1−2 = mµ 2i R∆T1−2 = 2i V1 (p2 − p1 ),

A1−2 = 0.

2) При изобарном процессе на основе I начала термодинамики теплота идет как на изменение внутренней энергии, так и на работу:

Q2−3 = ∆U2−3 + A2−3 ; A2−3 = p2 (V2 −V1 );

∆U

−3

R∆T

−3

−V );

−3

= p

−V )

+1 .

За оба процесса:

∆U = ∆U1−2 + ∆U2−3 = 2i V1(p2 − p1 )+ 2i p2 (V2 −V1 )= 2,5 102 Дж,

A = A2−3 = p2 (V2 −V1 )= 6,5 102 Дж,

Q =Q1−2 +Q2−3 = 2i V1(p2 − p1 )+ 2i +1 p2 (V2 −V1 )=9 102 Дж.

Задача 5 . Определить отношение γ = Ср для смеси 3 молей ар-

Сv

гона и 5 молей кислорода.

Дано:

ν1 = 3 моля

ν2 = 5 молей

µ1 = 40·10–3 кг/моль µ2 = 32·10–3 кг/моль

i1 = 3 i2 = 5

γ = ?

Решение

По определению молярные теплоемкости Cµp и CмV соответственно равны:

Cмp = нQ∆T = ∆нU∆+TA ;

CмV = нQ∆T = н∆∆UT .

Общее количество теплоты, затраченное на нагревание смеси из аргона и кислорода, найдем как сумму теплоты, затраченной на нагревание каждого газа в отдельности, а число молей смеси – как сумму молей аргона и кислорода, тогда

Cµ p =

Q1 +Q2

∆U1 + A1 +∆U2 + A2

(н

+ н

)∆T

(н + н

)∆T

R∆T +(p∆V ) + н

R∆T +(p∆V )

1 2

(н1 + н2 )∆T

R∆T + н R∆T + н

R∆T + н

R∆T

1 2

(н1 + н2 )∆T

+ н

+1 R

;

н1 + н2

CмV =

Q1′ +Q2′

∆U1 + ∆U2

(н + н

)∆T

(н

+ н

)∆T

R∆T

+ н

R∆T

н1

н2

;

(н1 + н2 )∆T

н1 + н2

+1 н

γ =

=1,47.

+ н

1 2

Ответ: 1,47.

Задача 6 . Температура пара, поступающего в паровую машину, t1 = 130 °С; температура в конденсаторе t2 = 25 °С. Определить теоретически максимальную работу при затрате количества теплоты Q = 5,1 кДж.

Дано:	Решение
T1 = 403 °К	Коэффициент полезного действия					цикла
Т2 = 298 °К	Карно
Q1 = 5,1·103 Дж	η =	T1 −T2			.	(1)

А = ?		T1
	КПД любого теплового двигателя
	η=		A	,		(2)


			Q
	1

где А – полезная работа, совершаемая двигателем;

Q1 – количество теплоты, полученное рабочим телом от нагревателя. Приравнивая правые части равенств (1) и (2), получим

A = T1 −T2 ,

Q1 T1

откуда

A = Q1 (T1 −T2 )=1,3 кДж. T1

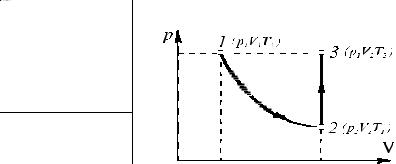
Задача 7. Кислород, масса которого т = 160 г при температуре t1 = 27 °С расширяется изотермически, а затем изохорно нагревается до t2 = 127 °С. Найти изменение энтропии, если известно, что начальное и конечное давления одинаковы.

Дано: Решение

т = 1,16 кг µ = 32·10–3 кг/моль i = 5

Т1 = 300 °К Т2 = 400 °К

S3 – S1 = ?

Для процессов 1–2–3 изменение энтропии

1 2

3 dQ

−S =

∫

V ,

(1)

где dQ = dA = p dV ,

= m C

dT.

Подставляя выражения dQT и dQV в выражение (1) и учитывая, что

при изотермическом процессе

p =

p1V1

mRT1

, получим:

µV

−S =

2 dV

3 dT

R ln

∫

2 .

1 V

Учитывая, что р1 / р2 = V2 / V1 (для процесса 1–2) и р1 / р2 = T2 / T1 (для процесса 2–3), получим V2 / V1 = T2 / T1, тогда

S		− S	=	m		i + 2	R ln	T2	= 41,9	Дж	.
S		− S	=	µ			R ln	T2	= 41,9		.
	3	1		µ	2			T		К
								1

Задача 8 . 14 г азота адиабатически расширяются так, что давление уменьшается в 5 раз, а затем изотермически сжимаются до первоначального давления. Найти приращение энтропии при этих процессах.

Дано:			Решение
dQ1 = 0	Приращение энтропии можно найти по фор-
т = 1,4·10–4 кг	мулам
µ = 28·10–3 кг/моль			∆S = ∫ dQ			;
р1/р2 = 5			∆S = ∫ dQ			;
Т2 = соnst				T
Т2 = соnst			∆S = ∆S1 + ∆S2 ;
∆S = ?			∆S = ∆S1 + ∆S2 ;
	∆S =	∫	dQ1 ;	∆S	2	=	∫	dQ2 ,
	∆S =		dQ1 ;	∆S		=		dQ2 ,
	1		T					T
								2

где ∆S1 – приращение энтропии при адиабатическом процессе; ∆S2 – приращение энтропии при изотермическом процессе.

Так как dQ1 = 0 по условию задачи, то и ∆S1 = 0. Чтобы найти ∆S2 запишем, чему равно количество теплоты dQ2, которое при изотермическом процессе полностью расходуется на работу, т. е. dQ2 = pdV. Отсюда

∆S2 = ∫	p dV	.	Используя уравнение Менделеева-Клапейрона выразим

	T
	2

давление через температуру и объем и подставим вместо р под интеграл. Тогда

mRdV

=5,7 102

Дж

∆S2 = ∫

R ln

µV

∆S = ∆S2.

Задача 9 . Найти приращение энтропии ∆S при расширении 2 г водорода от V1 = 1,5 л до V2 = 4,5 л, если процесс расширения происходит: 1) при постоянном давлении; 2) при постоянной температуре.

Дано:

i = 5

т = 2·10–3 кг

µ = 2·10-3 кг/моль V1 = 1,5·10–3 м3 V2 = 4,5·10–3 м3

1)р = соnst

2)Т = соnst

∆S1 = ? ∆S2 = ?

Решение

Используя формулу для приращения энтропии ∆S = ∫ dQT , найдем ∆S1 и ∆S2 , выра-

зив dQ из I начала термодинамики сначала для изобарического, а затем для изотермического процессов:

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025233.98 Кб0Seti_1.doc
#
22.11.2019141.82 Кб5shpory_po_BUDIS.doc
#
22.11.2019171.01 Кб5shpory_po_ekonomike.doc
#
17.03.2015344.58 Кб9ShPOR_FILOSOFIYa_33 (1).doc
#
17.03.20151.51 Mб58Slinkina_Mekh_i_mol_fiz_1.pdf
#
17.03.20151.07 Mб78Slinkina_Mekh_i_mol_fiz_2.pdf
#
16.09.2019286.39 Кб4SODERZhANIE_PRIChIN_ALKOGOLYa (1).docx
#
17.03.2015247.25 Кб6sotsiаlynаya_filosofiya.pdf
#
01.03.202510.24 Mб0Spetsglavy_2_redakt.doc
#
01.05.2025298.67 Кб0SRO_po_mikrobiologii_docx_izm.docx
#
22.07.2019249.46 Кб1StudentBank.ru_29836.rtf