
Slinkina_Mekh_i_mol_fiz_2
.pdf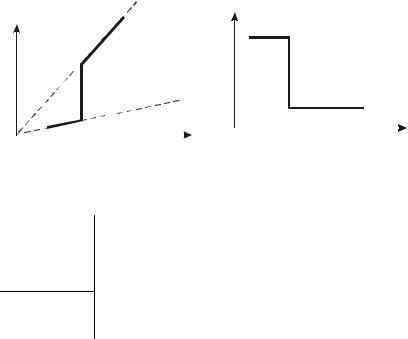
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
m2 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
µ |
µ |
2 |
|
RT |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
V = |
|
|
1 |
|
|
|
|
|
, |
|
|
|
|
||||
и тогда |
|
|
|
|
|
|
|
|
|
|
pсм |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
(m1 +m2 )pсм |
|
|
|
(4 10−3 |
|
|
|
10−3 )9,31 104 |
|
|
||||||||||||||
|
|
|
|
|
+32 |
3 |
|
||||||||||||||||||
ρсм |
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0,48 |
кг/м |
. |
m m |
|
|
|
4 10−3 |
|
32 |
10−3 |
|
|||||||||||||||||
|
|
|
1 |
+ |
2 |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
8,31 280 |
|
|
|
|
|
|
µ1 |
|
RT |
|
|
|
2 10 |
−3 |
32 |
10 |
−3 |
|
|
|
|
||||||||
|
|
|
|
µ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Задача 3 . Дан график зависимости объема идеального газа от температуры. По этой известной зависимости построить графики в осях
р – Т.
Расшифруем, графики каких процессов показаны на осях: 1—2 – изобарический процесс (р1 = const);
2—3 – изотермический процесс;
3—4 – изобарический процесс (р2 = const, но р2 < p1). Вычертим графики этих же процессов на других осях:
|
4 |
|
|
|
|
V |
p |
1 |
2 |
|
|
|
|
|
|
||
|
3 |
|
|
|
|
1 |
2 |
|
3 |
4 |
T |
T |
|
||||
|
|
|
|
||
|
|
|
|
|
Задача 4 . Открытый сосуд с газом нагрели от 27 °С до 127 °С. Определить, как изменилась масса газа в сосуде. Изменением размеров сосуда при нагревании пренебречь.
Дано:
Т1 = 300 °К
Т2 = 400 °К
V1 = V2 = V0
m2 =? m1
Решение
При нагревании открытого сосуда с газом в сосуде остаются постоянными давление и объем сосуда. Процесс перехода газа из одного состояния в другое является изобарным, но воспользоваться уравнением ГейЛюссака нельзя, так как меняется масса газа. Поэтому запишем уравнение Менделеева-Клапейрона (уравнение
76
состояния) для двух состояний газа:
p V = m1 |
RT , |
p V = |
m2 |
RT . |
||||||
|
||||||||||
0 |
0 |
|
µ |
1 |
|
0 |
0 |
µ |
2 |
|
откуда |
|
|
|
|
|
|
T1 |
|
|
|
m2 |
= |
T1 |
, |
m |
= m |
= 0,75 m . |
||||
m |
|
T |
|
2 |
|
1 |
T |
|
|
1 |
1 |
|
2 |
|
|
|
|
2 |
|
|
|
Задача 5 . В закрытом баллоне объема V1 = 2 л находится воздух, давление которого р1 = 0,53·105 Па при комнатной температуре. Затем баллон опускают в воду той же температуры и на глубине h = 1,2 м открывают. Какой объем воды V войдет в баллон, если атмосферное давле-
ние р0 = 0,99·105 Па?
Дано: |
|
|
|
|
|
|
|
|
Решение |
|
|
|
р1 = 0,53·105 Па |
|
|
|
|
Здесь имеет место изотермический процесс |
|||||||
V1 = 2 л = 2–3 м3 |
|
сжатия воздуха в баллоне. По закону Бойля- |
||||||||||
р0 = 0,99·105 Па |
|
Мариотта |
|
|
|
|
|
|
||||
h = 1,2 м |
|
|
|
|
|
|
|
|
p1V1 = p2V2 , |
|
|
|
ρ = 103 кг/м3 |
|
|
|
|
|
|
|
|
|
|
||
V = ? |
|
где р2 – давление на глубине h. |
|
|
|
|||||||
|
|
|
p |
2 |
= p +ρgh =1,10 105 Па. |
|
|
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
p1V1 |
|
|
|
|
−3 |
3 |
|
||
|
|
|
|
p1 |
|
|
||||||
V =V1 −V2 =V1 |
− |
|
|
|
=V1 1− |
|
|
=1,045 10 |
|
м =1,045 дм |
. |
|
|
p2 |
|
|
|||||||||
|
|
|
|
|
p2 |
|
|
|
|
|||
3 . 2 . ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Основные формулы
1. Распределение Больцмана (распределение частиц в силовом поле)
n = n0e−U kT ,
kT ,
где п – концентрация частиц;
U – их потенциальная энергия;
п0 – концентрация частиц в точках поля, где U = 0; k – постоянная Больцмана;
77

T – термодинамическая температура;
е– основание натуральных логарифмов.
2.Барометрическая формула (распределение давления в однородном поле силы тяжести)
p = p e−mgh /(kT ), или |
p = h e−µgh /(RT ), |
0 |
0 |
где р – давление газа; т – масса частицы; µ – молярная масса;
h – высота точки по отношению к уровню, принятому за нулевой; р0 – давление на этом уровне;
g – ускорение свободного падения;
R– универсальная газовая постоянная.
3.Вероятность того, что физическая величина х, характеризующая молекулу, лежит в интервале значений от х до х + dх, равна
dW (x)= f (x)dx,
где f (х) – функция распределения молекул по значениям данной физической величины х (плотность вероятности).
4. Количество молекул, для которых физическая величина х, характеризующая их, заключена в интервале значений от х до х + dх,
dN = NdW (x)= N f (x)dx.
5. Распределение Максвелла (распределение молекул по скоростям) выражается двумя соотношениями:
а) число молекул, скорости которых заключены в пределах от v до
v + dv,
|
m 3/ 2 |
−mv2 /(2kT ) |
|
2 |
|
||
dN(v)= N f (v)dv = 4πN |
|
|
e |
|
v |
|
dv, |
|
|
|
|||||
|
2πkT |
|
|
|
|
|
|
где f (v) – функция распределения молекул по абсолютным значениям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от v до v + dv, к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале;
N – общее число молекул; т – масса молекулы;
б) число молекул, относительные скорости которых заключены в пределах от и до и + dи,
dN(u)= N f (u)du = |
4 |
Ne−u2 u2du, |
|
π |
|
78 |
|
|
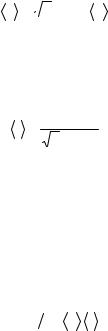
где u = v / vв – относительная скорость, равная отношению скорости v к
наивероятнейшей скорости vв;
f (и) – функция распределения по относительным скоростям.
6.Среднее число соударений, испытываемых одной молекулой газа
вединицу времени,
z =  2 πd 2n v ,
2 πd 2n v ,
где d – эффективный диаметр молекулы; п – концентрация молекул;
v – средняя арифметическая скорость молекул.
7. Средняя длина свободного пробега молекул газа
l = |
1 |
2 πd 2n . |
8. Импульс (количество движения), переносимый молекулами из одного слоя газа в другой через элемент поверхности,
dp = η(dv / dz)∆ S dt,
где η – динамическая вязкость газа;
dv / dz – градиент (поперечный) скорости течения его слоев; ∆S – площадь элемента поверхности; dt – время переноса.
9. Динамическая вязкость
η=1 3ρ v l ,
где ρ – плотность газа (жидкости);
v – средняя скорость хаотического движения его молекул;l – их средняя длина свободного пробега.
10. Закон Ньютона
F = dp / dt = η(dv / dz)∆S,
где F – сила внутреннего трения между движущимися слоями газа. 11. Закон Фурье
∆Q = −K (dT / dx)S ∆t,
где ∆Q – теплота, прошедшая посредством теплопроводности через сечение площадью S – за время ∆t;
К – теплопроводность; dT/dx – градиент температуры.
79

12. Теплопроводность (коэффициент теплопроводности) газа
K =1 3cV ρ v l , или K =1 6 kn v l ,
где сV – удельная теплоемкость газа при постоянном объеме; ρ – плотность газа;
v – средняя арифметическая скорость его молекулы;l – средняя длина свободного пробега молекул.
13. Закон Фука
∆m = −D (dn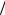 dx)m1S ∆t ,
dx)m1S ∆t ,
где ∆т – масса газа, перенесенная в результате диффузии через поверхность площадью S за время ∆t;
D – коэффициент диффузии;
dn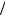 dx – градиент концентрации молекул; т1 – масса одной молекулы.
dx – градиент концентрации молекул; т1 – масса одной молекулы.
14. Коэффициент диффузии
D = 13 v l .
80
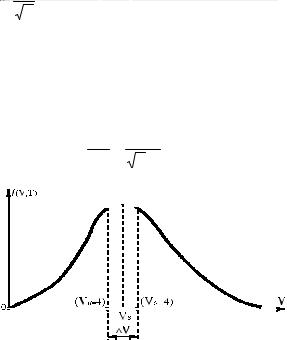
Примеры решения задач
Задача 1 . Какая часть молекул кислорода, находящегося при температуре Т = 300 °К, обладает скоростями, отличающимися от наиболее вероятной скорости не свыше, чем на 4 м/с.
Дано: |
|
|
|
|
|
|
Решение |
|
|
∆v = 8 м/с |
|
|
Закон распределения молекул по скоростям (закон |
||||||
Т = 300 °К |
|
Максвелла): число молекул ∆N, относительные скорости |
|||||||
|
|
|
которых лежат в интервале от u до u + ∆u, равно |
|
|||||
∆N |
=? |
|
|
||||||
|
|
|
|
|
|
∆N = N f (u) ∆u. |
|
||
N |
|
|
|
|
|
|
|
(1) |
|
|
Здесь N |
– полное число молекул газа, |
|
||||||
|
|
4 |
e |
−u2 |
u |
2 |
– функция распределения Максвелла, |
|
|
|
f (u)= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
u = v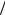 vв,
vв,
где v – данная скорость;
vв – наиболее вероятная скорость.
Уравнение (1) справедливо при условии ∆u << u. По условию задачи v = vв, следовательно, u = v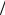 vв =1 и уравнение (1) примет вид
vв =1 и уравнение (1) примет вид
∆N |
= |
|
4 |
∆u. |
|||||
N |
|
|
|
π e |
|
||||
|
|
|
|
|
|
|
|
|
|
Сначала убедимся, что ∆u << u. Так как u = v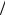 vв, то
vв, то
∆u = |
∆v . |
(2) |
|
vв |
|
81 |
|
|
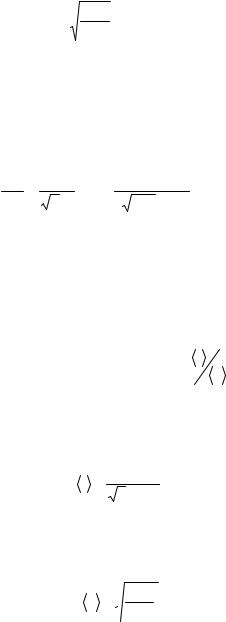
Определим теперь наиболее вероятную скорость
vв = |
2RT |
= 3,95 102 м/с. |
|
µ |
|
Подставляя это значение vв в (2) и имея ввиду, что ∆v = 8 м/с, поскольку в задаче идет речь о скоростях, лежащих в интервале от
(vв – 4) м/с до (vв + 4) м/с, получим
|
|
∆u = |
8 |
|
= 2,02 10−2 |
, |
|
|
3,95 102 |
||||
|
|
|
|
|
||
т. е. ∆u << u. |
|
|
|
|
|
|
∆N |
= |
4 |
∆u = |
4 2,02 10−2 |
|
|
N |
|
|
= 0,017. |
|||
|
π e |
|
3,14 2,7 |
|
||
Задача 2 . Найти среднюю продолжительность свободного пробега молекул кислорода при давлении 2 мм рт. ст и температуре 27 °С.
|
Дано: |
Решение |
|
р = 2 мм рт. ст. = 266 Па |
Средняя продолжительность свобод- |
||
Т = 300 °К |
|
|
ного пробега молекул равна отношению |
µ = 32 ·10–3 кг/моль |
l |
||
–10 |
м (из таблицы) |
||
σ = 2,9 ·10 |
|
v , |
|
τ = ? |
|
|
|
|
|
|
|
где l – средняя длина свободного пробега молекул;v – средняя арифметическая скорость молекул.
Среднюю длину свободного пробега молекул газа можно вычислить по формуле
l = |
kT |
, |
|
2πσ2 p |
|
где σ – эффективный диаметр молекул; k – постоянная Больцмана.
Средняя арифметическая скорость формуле
v =  8πµRT
8πµRT
молекул газа вычисляется по
.
82
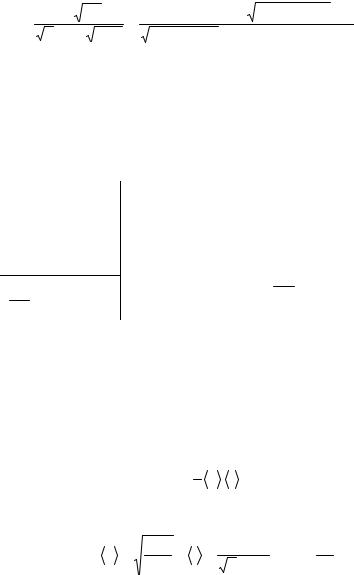
Тогда
τ = |
kT πµ |
= |
1,39 10−23 300 3,14 32 10−3 |
−8 |
c. |
|
2πσ2 p 8RT |
16 8,31 300 3,14 266 (2,9 10−10 )2 |
= 9,3 10 |
|
|||
Ответ: τ = 9,3 ·10–8 с.
Задача 3 . Пространство между двумя большими параллельными пластинами заполнено гелием. Расстояние между пластинами ∆l = 50 мм. Одна пластина поддерживается при температуре Т1 = 293 °К, другая при температуре Т2 = 313 К. Вычислить поток тепла q, приходящейся на единицу площади пластин, если давление в газе 760 мм рт.ст.
Дано:
∆l = 5 ·10–2 м
T1 = 293 °К
T2 = 313 К р = 105 Па
∆qS = ?
Решение
Из закона Фурье количество теплоты, прошедшее посредством теплопроводности через площадь ∆S за время ∆t, равно
Q= −K ∆T ∆S ∆t.
∆l
Поток тепла представляет собой количество тепла, прошедшее через площадь ∆S за единицу времени, поэтому
q |
|
Q |
|
− K |
∆T |
∆S ∆t |
|
ДT |
|
|
|
∆l |
= −K |
||||||
|
= |
|
= |
|
|
|
. |
||
∆S |
∆S ∆t |
|
∆S ∆t |
Дl |
|||||
Коэффициент теплопроводности
K = 1 |
v l ρ c , |
3 |
V |
|
где ρ – плотность гелия;
v = |
8RT |
; |
l = |
kT |
; cV = iR . |
|
πµ |
|
|
2πσ2 p |
2µ |
Плотность гелия при данных условиях можно найти, пользуясь уравнением Менделеева–Клапейрона
83
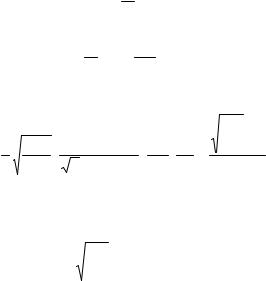
pV = mµ RT,
откуда
Vm =ρ = RTpµ .
Подставив выражения для v , l , cV и ρ выразим К:
|
|
|
|
|
|
|
iR |
|
RT |
iR |
K = |
1 |
8RT |
|
RT |
|
pµ |
= |
πµ |
, |
|
|
3 |
πµ |
|
2 πσ2 pN A |
|
RT |
2µ |
3 |
πσ2 N A |
|
где T =T1 +T2 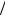 2.
2.
Тогда поток тепла через единичную площадь будет равен
|
|
iR |
RT |
(T −T ) |
||||
q |
= |
|
πµ |
2 |
1 |
= 20 |
Bт |
. |
|
|
3 πσ2 N A ∆l |
|
|
||||
∆S |
|
|
|
|
м2 |
|||
84
4. ТЕРМОДИНАМИКА
4 . 1 . ФИЗИЧЕСКИЕ ОСНОВЫ ТЕРМОДИНАМИКИ
Основные формулы
1. Связь между молярной (Сµ) и удельной (с) теплоемкостями газа
Cµ = cµ,
где µ – молярная масса газа.
2. Молярные теплоемкости при постоянном объеме и постоянном давлении соответственно равны
CV = iR / 2, Cp = (i + 2)R / 2,
где i – число степеней свободы;
R– универсальная газовая постоянная.
3.Удельные теплоемкости при постоянном объеме и постоянном давлении соответственно равны:
cV = 12 µR , cp = i +22 µR .
4. |
Уравнение Р. Майера |
|
|
|
|
||
|
|
|
|
Cp −CV |
= R. |
|
|
5. |
Показатель адиабаты |
|
|
|
|
||
|
γ = c |
p |
c , или |
г =C |
p |
C , или |
γ = i +2 . |
|
|
V |
|
V |
i |
||
|
|
|
|
|
|
|
|
6. Внутренняя энергия идеального газа
U = N ε , или U = нCV T,
где ε – средняя кинетическая энергия молекулы; N – число молекул газа;
ν – количество вещества.
∆U = 2i mµ R (T2 −T1 ) – изменение внутренней энергии.
85
