Шаг 1: Формулировка основной и альтернативной гипотезы
Нулевая гипотеза (H0) – утверждение о параметре генеральной совокупности (параметрах генеральных совокупностей) или распределении, которое необходимо проверить.
Альтернативная гипотеза (HA) – утверждение, противоположное нулевой гипотезе. Выдвигается, но не проверяется
H0: мужчины и женщины пользуются интернетом с одинаковой частотой.
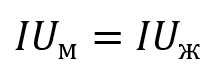
HА: мужчины и женщины пользуются интернетом с разной частотой.
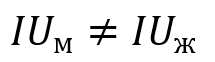
Виды альтернативных гипотез
• Односторонняя: H1 утверждает, что разница или эффект существует в определенном направлении (например, больше, меньше).
• Двусторонняя: H1 утверждает, что разница или эффект существует в любом направлении (например, отличается).
Шаг 2: Выбор уровня значимости
Уровень значимости (α) – вероятность отвергнуть верную нулевую гипотезу. Нулевая гипотеза всегда проверяется на определенном уровне значимости. Например, если мы проверяем нулевую гипотезу на уровне значимости 5%, это означает, что если мы будем проводить аналогичные исследования 100 раз и проверять на основе имеющихся данных интересующую нас нулевую гипотезу, в 5 случаях из 100 мы отвергнем нулевую гипотезу, хотя она будет верной.
β – вероятность того, что ложная нулевая гипотеза будет принята.
Уровни значимости, принятые в маркетинговых исследованиях:
α – уровень значимости
0,01 (1%)
0,05 (5%)
(1-α) – уровень доверия (доверительная вероятность)
0,99 (99%)
0,95 (95%)
Шаг 3: Определение статистического критерия
Критерий χ2 (хи-квадрат) используется для проверки статистической значимости взаимосвязей между переменными, наблюдаемых в перекрестных таблицах. Он помогает нам определить, являются ли различия между наблюдаемыми и ожидаемыми данными случайными или они указывают на наличие статистически значимой разницы.
H0: взаимосвязи между переменными нет
Тест χ2 проверяет равенство частотных распределений:
fо – ожидаемые частоты (расчётные значения), которые бы стояли в ячейках, в случае когда связи между переменными нет.
fн – реально наблюдаемые частоты, т.е. значения, которые стоят в составленной нами таблице
Расчёт χ2 следует производить только на основе абсолютных значений частот. Если исходные данные представлены в процентах, то их необходимо пересчитать а абсолютные частоты.
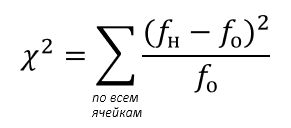
В нашем примере:
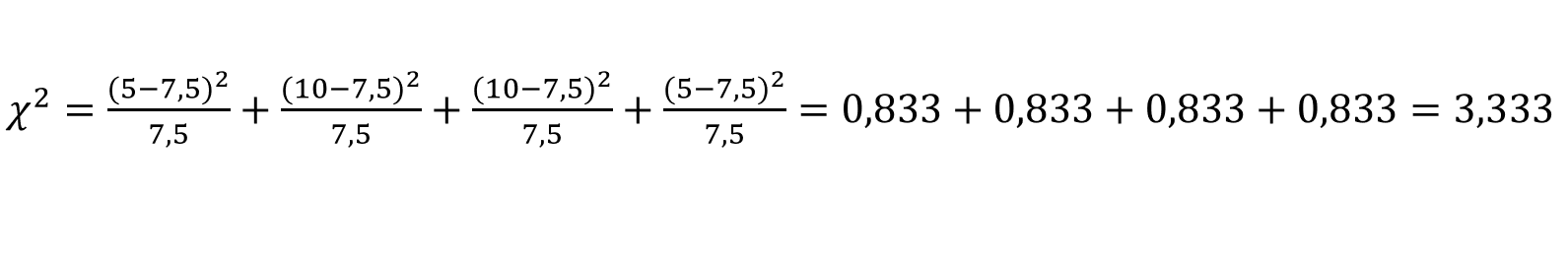
Шаг 4: Формулировка правила принятия решения
Kн – наблюдаемое (расчётное) значение статистического критерия.
Kкрит– критическое значение статистического критерия для заданного уровня значимости.
Если Kн меньше уровня значимости (α), то H0 надо отклонить.
Если Kн больше критического значения (Kкрит), то H0 принимается.
Таблица критических значений χ2 для различных α
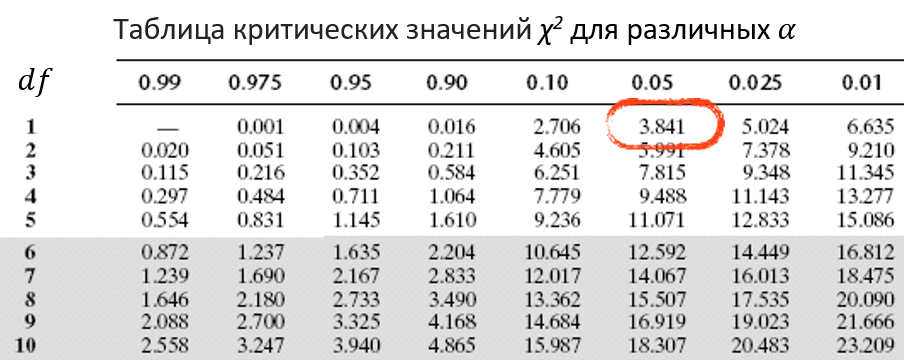
df=(r-1)(c-1)
df - количество степеней свободы r – количество строк c – количество столбцов
df=(2-1)(2-1)=1
H0 не может быть отклонена
Шаг 5: Принятие решения
Нашлись ли доказательства? Что из этого следует?
- H0 отсутствия различий не может быть отклонена
- Различия не являются статистически значимыми на уровне 0,05
- Полученные на выборке результаты не могут быть обобщены на генеральную совокупность
Пол и частота пользования интернетом
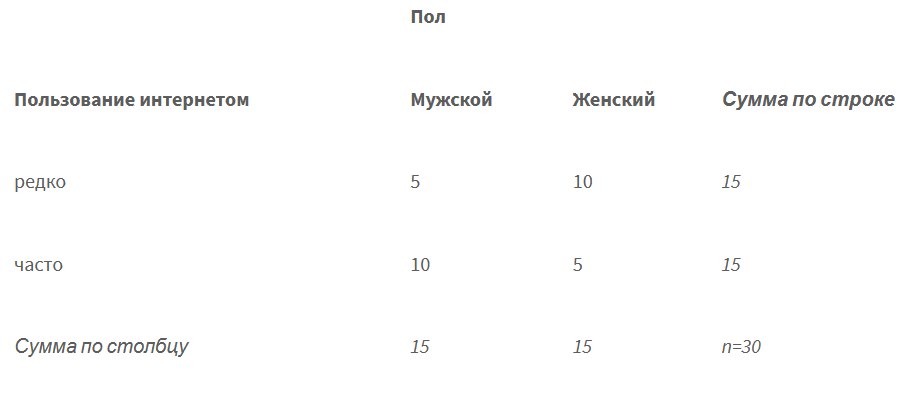
Можем ли мы на основании этой выборки утверждать, что во всем населении среди мужчин больше активных интернет пользователей, чем среди женщин?
Ответ:
Данная выборка не дает оснований для таких утверждений. Если выборка была произведена должным образом, то мы можем с 95% доверительной вероятностью констатировать, что взаимосвязи между полом и частотой пользования интернетом нет. В противном случае – мы не знаем ответа.