10. Определение корреляции в данных. Свойства коэффициента корреляции. Формула для нахождения коэффициента корреляции.

Корреляция — это мера взаимосвязи между двумя величинам.

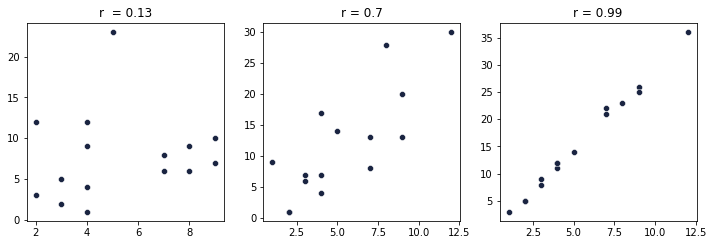
Если два признака линейно взаимосвязаны, то мы говорим, что они коррелируют. Например, чем больше студент посещает лекции — тем выше у него будет оценка за дисциплину. Значит, признак «посещаемость лекций» будет коррелировать с признаков «оценка за дисциплину». Сила корреляции (взаимосвязи) выражается числом, которое называется коэффициентом корреляции. Например, на данных рисунках можно видеть линейную, квадратичную и кубическую взаимосвязи:

Свойства коэффициента корреляции

1. Изменяется от −1 до 1 (чем ближе коэффициент корреляции по модулю к 1, тем сильнее связь.)

Ориентировочно можно делать выводы согласно классификации, которую предложил математик Чеддок: слабая — от 0.1 до 0.3; умеренная — от 0.3 до 0.5; заметная — от 0.5 до 0.7; высокая — от 0.7 до 0.9; весьма высокая (сильная) — от 0.9 до1.0. Отрицательная корреляция означает, что две переменные изменяются в противоположных направлениях: при увеличении одной переменной другая уменьшается, и наоборот. Примеры отрицательной корреляции: Уровень образования и преступность: чем выше уровень образования, тем ниже уровень преступности в данном регионе.

Визуально можно примерно определить, сильная или слабая связь по тому, насколько точки на диаграмме рассеяния стремятся выстроиться в одну линию. При отсутствии корреляции точки представляют собой просто неупорядоченное хаотичное множество, при более сильной уже видна тенденция на линейную взаимосвязь, а при сильной — уже выстраивается практически четкая линия из точек.

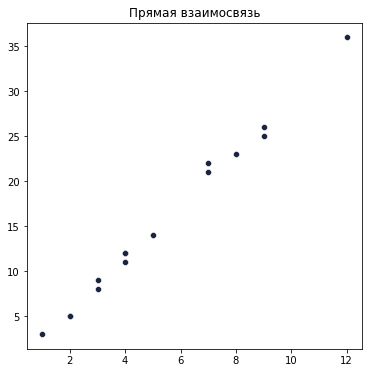
2. Положительный коэффициент корреляции свидетельствует о прямой зависимости.

По мере увеличения роста человека обычно увеличивается и его вес. То есть, когда значение одного признака увеличивается, то значение другого тоже увеличивается.

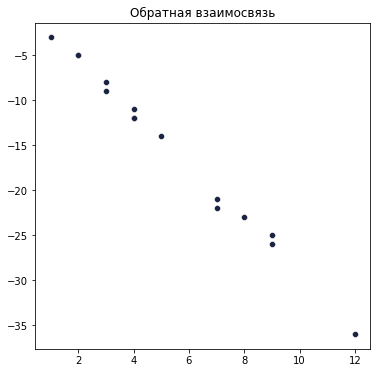
3. Отрицательный коэффициент корреляции свидетельствует об обратной зависимости.

Обратную зависимость можно наблюдать между количеством работы и количеством сна. Чем больше количество работы — тем меньше количество сна. И чем больше количество сна — тем меньше количество работы. То есть, когда значение одного признака увеличивается, то значение другого уменьшается:

Для того чтобы оценить силу и направление линейной взаимосвязи, мы будем рассчитывать коэффициент корреляции Пирсона (обычно его обозначают маленькой буквой r) по следующей формуле:

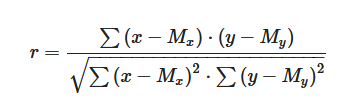
(Для запоминания: в числителе сумма произведений, в знаменателе произведение суммы каждая из которых в квадрате и под корнем)

Пусть у нас есть две переменные Х и У, для которых мы хотим вычислить коэффициент корреляции:

X	Y
2	6
4	8
1	1
3	7
5	3

Вычислим среднее значение для переменной X:

(2+4+1+3+5)/5=3

Теперь из каждого значения X вычтем среднее значение и возведем полученную разность в квадрат:

X	X−Mx	(X−Mx)2
2	2 - 3 = -1	1
4	4 - 3 = 1	1
1	1 - 3 = -2	4
3	3 - 3 =0	0
5	5 - 3 =2	4

Сумма разностей значений X и средних в квадрате равна:

1+1+4+0+4=10

Теперь вычислим среднее значение для переменной Y:

(6+8+1+7+3)/5=5

Теперь из каждого значения Y вычтем среднее значение и возведем полученную разность в квадрат:

Y	Y−MY	(Y−MY)2
6	6 - 5 = 1	1
8	8 - 5 = 3	9
1	1 - 5 = -4	16
7	7 - 5 = 2	4
3	3 - 5 = -2	4

Сумма разниц в квадрате равна:

1+9+16+4+4=31

Перемножим значения двух столбцов с разницами:

X−Mx	Y−MY	(X−Mx)⋅(Y−y)
-1	1	-1
1	3	3
-2	-4	8
0	2	0
2	-2	-4

Теперь сложим все произведения:

−1+3+8+0–4=6

Вычисляем коэффициент корреляции. В числителе у нас будет сумма произведений, которую мы посчитали в строке выше (то есть, 6). А в знаменателе будет корень из произведения суммы квадратов ( 10 и 31). То есть, корень из 310. Получаем:

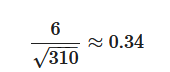
Итак, мы вычислили, что коэффициент корреляции между двумя признаками равен примерно 0.34, если округлять до сотых. То есть, между этими двумя признаками есть умеренная положительная связь. При корреляционном анализе мы оцениваем общую тенденцию, поэтому при изменениях одной из переменной, которые не влияют на общий паттерн, коэффициент корреляции не будет меняться.