4. Визуализация данных. Линейный график, столбчатые диаграммы, гистограммы, диаграммы рассеяния. Изобразить графически, описать суть графиков.

Визуализация данных - это представление данных в виде, который обеспечивает наиболее эффективную работу человека по их изучению.

Линейный график

Линейная диаграмма или линейный график, также известный как кривая диаграмма - тип диаграммы, которая отображает информацию в виде ряда точек данных, называемых "маркерами", соединенных отрезками прямой линии.

Линейный график (или линейная диаграмма) показывает динамику по одному либо нескольким показателям. Его удобно применять, когда нужно сравнить, как меняются с течением времени разные наборы данных.

Столбчатая диаграмма - диаграмма, представленная прямоугольными зонами, высоты или длины которых пропорциональны величинам, которые они отображают. Прямоугольные зоны могут быть расположены вертикально или горизонтально. Столбчатая диаграмма отображает сравнение нескольких дискретных категорий.

Столбчатые диаграммы используются для отображения результатов сравнения одного показателя в разных условиях (например, результатов социологических опросов).

Столбчатые диаграммы необходимо представлять в виде отдельных столбиков одинаковой ширины, поскольку они представляют дискретные данные, и никогда не должны связываться линией.

Гистограмма - способ представления табличных данных в графическом виде - в виде столбчатой диаграммы. Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны.

Гистограммы используют для представления числовых данных одной категории и их изменения с течением времени. Пример — изменение численности населения страны за конкретный период.

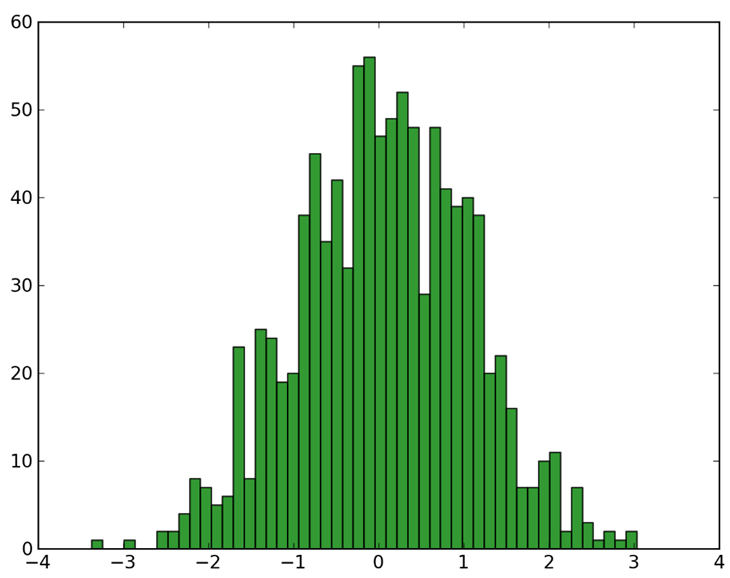
Различия между Линейный график и полигон частот:

• Линейный график показывает тенденции и закономерности, а полигон частот подчеркивает форму распределения.

Различия между Гистограмма и столбчатая диаграмма:

• Гистограмма используется для непрерывных данных, разбитых на интервалы, а столбчатая диаграмма — для категориальных данных.

• Прямоугольники в гистограмме не имеют промежутков между ними, а столбцы в столбчатой диаграмме имеют промежутки.

Диаграммы рассеяния (другие названия – диаграмма разброса, диаграмма рассеивания, поле корреляции) - Математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. Могут использоваться и полярные координаты.

Диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.

В зависимости от наличия или отсутствия предполагаемых причинно-следственных связей при помощи диаграммы рассеяния можно анализировать зависимость:

•между влияющим фактором (причиной) и характеристикой (следствием);

•между двумя характеристиками;

•между двумя факторами.

5. Меры вариативности. Перечислить основные типы, написать формулу для нахождения. Какие меры вариативности подвержены выбросам в данных? Подтвердите выводы на примере.

Классный тест по вопросу по ссылке

Меры вариативности (разброса) - количественные меры, выражающие различия между значениями в распределении. Более формально — это степень индивидуальных отклонений значений от центральной тенденции. Вариативность также помогает нам понять, насколько типичной для распределения является случайно взятая оценка. Если вариативность маленькая — то значения больше похожи друг на друга.

Рассчитаем меры вариативности для переменной X= [3,5,6,7,4,6,5,4,6]:

Размах (range) - это разность между максимальным и минимальным значением признака:

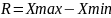
R = 7 - 3 = 4. Таким образом мы отразим максимальную разницу в значениях среди нашей выборки. На основании размаха мы можем судить о близости имеющихся значений или наличии выбросов.

Квартили — это значения, которые делят распределение на четверти.

• Первый квартиль (еще его называют нижним) — отделяет первые 25% значений от следующих 75%.

• Второй квартиль (он же медиана) — делит выборку пополам (50% и 50%).

• Третий квартиль (еще его называют верхним) — отделяет первые 75% выборки от следующих 25%.

• Четвертый квартиль по сути уже не делит выборку — ниже него располагается 100% значений.

Возможно, вы еще встречали такое понятие как персентиль или процентиль — это такое значение переменной ниже которого находится определенный процент наблюдений в наших данных. Если указано, что нужно попасть в 95-й персентиль – это значит, что ваш балл за тест должен быть лучше, чем у 95% сдававших в этот год.

Интерквартильный размах — интервал значений признака, содержащий центральные 50% наблюдений распределения, то есть интервал между первым и третьим квартилем: 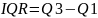Он показывает диапазон, в который попадает средняя половина данных.

X=[3,5,6,7,4,6,5,4,100]. Мы уже работали с этим примером и видели, что простой размах получается для нее не очень релевантным.

1. Отсортируем данные в порядке возрастания: [3, 4, 4, 5, 5, 6, 6, 7, 100]

3. Нижний квартиль (Q1) - это медиана нижней половины данных. Нижняя половина: [3, 4, 4, 5]. Медиана нижней половины равна 4.

4. Верхний квартиль (Q3) - это медиана верхней половины данных. Верхняя половина: [6, 6, 7, 100]. Медиана верхней половины равна 6,5.

Интерквартильный размах (IQR) = Q3 - Q1 = 6,5 - 4 = 2,5

Дисперсия - это мера того, насколько сильно значения в наборе данных разбросаны относительно среднего значения. Дисперсия показывает, насколько в среднем все значения выборки отклоняются от среднего значения по выборке.

Формула дисперсии.

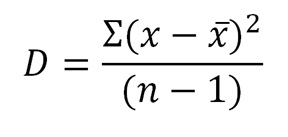
Мы видим, что в числителе стоит сумма отклонений каждого из наблюдений (х-x̅) (само число – среднее значение) еще и возведенная в квадрат, а в знаменателе — количество этих самых наблюдений.

Дисперсия характеризует то, насколько индивидуальные значения отклоняются от среднего. Но в силу того, что она всегда представляет собой квадрат нужных нам единиц, оперировать ей не так удобно как стандартным отклонением.

Значит сейчас надо просто найти корень из того, что получилось. Таким образом мы получим стандартное отклонение (оно же среднеквадратичное). Если бы мы работали с генеральной совокупностью, оно называлось бы сигмой (σ).

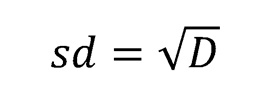
Стандартное отклонение (standart deviation) - это число, на которое отличаются все индивидуальные значения от среднего арифметического в выборке.