3. Частотные распределения. Разница между нормальным и равномерным распределением. Приведите пример визуализации графика распределения для своего набора данных.
Частотное распределение — метод статистического описания данных (измеренных значений, характерных значений). Частотное распределение можно представить не только в виде таблицы, но и визуализировать его. Для этого есть два типа диаграмм: гистограмма и полигон.
Гистограмма (очень простыми словами) - ряд прямоугольников, которые показывают, сколько наблюдений попадает в каждый интервал.
Для построения гистограммы по оси абсцисс (оси X) откладываются все возможные значения, а по оси ординат (оси Y) — частоты.
Значение |
Частота |
2 |
5 |
3 |
10 |
4 |
6 |
5 |
4 |
Однако важно помнить, что ее можно построить только для количественных данных.
Полигон (очень простыми словами) - линия, которая соединяет точки данных и показывает общую форму распределения.
Для этого нам необходимо отметить точки на области построения, которые соответствуют высоте столбца (как если бы мы строили гистограмму) и соединяем точки.
Гистограмма отлично подходит для визуализации количественных данных, но нам важно уметь в аналогичном виде представлять распределение частот для порядковых и номинальных данных. Аналогом гистограммы для качественных данных является столбчатая диаграмма. Для ее построения нужны ровно те же действия, что и для гистограммы, но визуально она немного отличается: между столбцами для разных категорий есть расстояние.
Нормальное распределение – это такое распределение, в котором крайние значения некоторого признака – наименьшее и наибольшее – появляются редко; чем ближе значение признака к математическому ожиданию (сумма произведений значения на его вероятность), тем чаще оно встречается.
Он имеет следующие свойства:
• Симметричный
• Колоколообразный
Равномерное распределение — это такое распределение вероятностей, при котором каждое значение в интервале от a до b равновероятно.
Он имеет следующие свойства:
•Симметричный
•прямоугольной формы
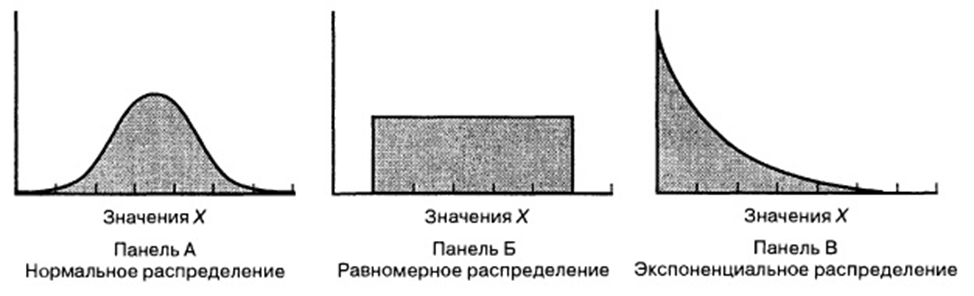
Нормальное распределение и равномерное распределение имеют следующее сходство:
• Оба распределения симметричны. левая и правая стороны распределения были бы идеально зеркальны друг другу
Однако эти два дистрибутива имеют следующее различия:
• Распределения имеют разную форму.
• Нормальное распределение имеет колоколообразную форму, что означает, что значения вблизи центра распределения более вероятны, чем значения в хвостах распределения.
• Равномерное распределение имеет прямоугольную форму, что означает, что каждое значение в распределении встречается с одинаковой вероятностью.
В равномерном вероятность попасти на любой участок равной меры (длины, площади итд) - одинакова, в нормальном - вероятность больше около центра, по мере удаления - быстро убывает.
Нормальное распределение используется для моделирования явления, которое имеет тенденцию следовать форме «колоколообразной кривой». Например, что вес новорожденных при рождении обычно распределяется со средним значением около 7,5 фунтов. Гистограмма массы тела при рождении новорожденных в США имеет колоколообразную форму, которая обычно имеет нормальное распределение:
Большинство младенцев, вероятно, будут весить около 7,5 фунтов, при этом немногие весят менее 7 фунтов, а немногие - более 8 фунтов.
И наоборот, равномерное распределение используется для моделирования сценариев, в которых каждый потенциальный результат равновероятен.
Классический пример — бросание игральной кости. Если вы бросаете игральную кость один раз, вероятность того, что она выпадет на число от 1 до 6, будет равномерно распределена, потому что все числа выпадут с одинаковой вероятностью.
Например, существует 6 возможных чисел, на которые может выпасть кубик, поэтому вероятность того, что выпадет 1 и другие варианты = 1/6.