26. Алгоритм knn. Для решения каких задач применяется алгоритм? Формула нахождения Евклидового расстояния. Опишите порядок действий при работе алгоритма.

К-ближайших соседей (K-Nearest Neighbors или просто KNN) — алгоритм классификации и регрессии, основанный на гипотезе компактности, которая предполагает, что расположенные близко друг к другу объекты в пространстве признаков имеют схожие значения целевой переменной или принадлежат к одному классу.

• В случае использования метода для классификации объект присваивается тому классу, который является наиболее распространённым среди k соседей данного элемента, классы которых уже известны.

• В случае использования метода для регрессии, объекту присваивается среднее значение по k ближайшим к нему объектам, значения которых уже известны.

На интуитивном уровне суть метода проста: посмотри на соседей вокруг, какие из них преобладают, таковым ты и являешься. Формально основой метода является гипотеза компактности: если метрика расстояния между примерами введена удачно, то схожие примеры гораздо чаще лежат в одном классе, чем в разных.

• Евклидова метрика (евклидово расстояние) – это наиболее простая и общепринятая метрика, которая определяется как длина отрезка между двумя объектами a и b в пространстве с n признаками и вычисляется по формуле: Проще говоря, это наименьшее возможное расстояние между точками A и B.

Хотя евклидово расстояние полезно для малых измерений, оно не работает для больших измерений и для категориальных переменных. Недостатком евклидова расстояния является то, что оно игнорирует сходство между атрибутами. Каждый из них рассматривается как полностью отличный от всех остальных.

Формула вычисления евклидова расстояния:

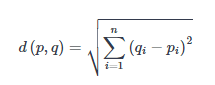
• Другой важной составляющей метода является нормализация. Разные атрибуты обычно обладают разным диапазоном представленных значений в выборке. К примеру, атрибут А представлен в диапазоне от 0.01 до 0.05, а атрибут Б представлен в диапазоне от 500 до 1000). В таком случае значения дистанции могут сильно зависеть от атрибутов с бо́льшими диапазонами. Поэтому данные в большинстве случаев проходят через нормализацию. При кластерном анализе есть два основных способа нормализации данных: MinMax-нормализация и Z-нормализация.

Порядок действий при работе алгоритма:

• Инициализируйте k путем выбора оптимального числа соседей.

• Для каждого образца в данных:

1. Вычислите расстояние между примером запроса и текущим примером из данных.

2. Добавьте индекс образца в упорядоченную коллекцию, как и его расстояние.

• Отсортируйте упорядоченную коллекцию расстояний и индексов от наименьшего до наибольшего, в порядке возрастания.

• Выберите первые k записей из отсортированной коллекции.

• Итоговым прогнозом среди выбранных k-ближайших образцов будет мода в случае классификации и среднее арифметическое в случае регрессии;

27. Алгоритм Random Forest. Для решения каких задач применяется алгоритм? Формула итогового классификатора. Порядок действий в алгоритме. Назовите критерии расщепления. Назовите важные параметры для работы алгоритма и объясните их суть.

Случайный лес — это алгоритм обучения с учителем. Он имеет два варианта: один используется для задач классификации, а другой — для задач регрессии. Он создает деревья решений на основе заданных выборок данных, получает прогноз от каждого дерева и выбирает лучшее решение посредством голосования. Алгоритм случайного леса объединяет несколько деревьев решений, в результате чего образуется лес деревьев. В классификаторе случайных лесов чем больше деревьев в лесу, тем выше точность.

Алгоритм Random Forest работает аналогично:

1. Он создает множество "деревьев решений", которые являются схожими деревьями решений. Каждое дерево обучается на разных подмножествах ваших данных и с использованием разных наборов признаков.

2. Когда вам нужно принять решение, каждое дерево "голосует" за лучший вариант на основе своих знаний.

3. Алгоритм объединяет голоса всех деревьев, чтобы определить окончательное решение.

Работу алгоритма Random forest можно разделить на 2 этапа

На первом этапе мы действуем следующим образом:

• Случайным образом выберите k объектов из общего числа m объектов, где k < m.

• Среди функций «k» вычислите узел «d», используя лучшую точку разделения.

• Разделите узел на дочерние узлы, используя наилучшее разделение.

• Повторяйте шаги от 1 до 3, пока не будет достигнуто количество узлов l.

• Постройте лес, повторяя шаги с 1 по 4 n количество раз, чтобы создать n деревьев.

На втором этапе мы делаем прогнозы, используя обученный алгоритм случайного леса.

• Мы берем функции теста и используем правила каждого случайно созданного дерева решений для прогнозирования результата и сохраняем прогнозируемый результат.

• Затем мы подсчитываем голоса для каждой прогнозируемой цели.

• Наконец, мы рассматриваем предсказанную цель с наибольшим количеством голосов как окончательный прогноз алгоритма случайного леса.

Преимущества алгоритма случайного леса заключаются в следующем:

• Она считается очень точной и надежной моделью, поскольку для прогнозирования использует большое количество деревьев решений.

• Случайные леса принимают среднее значение всех прогнозов, сделанных деревьями решений, что нивелирует предвзятости. Таким образом, он не страдает от проблемы переобучения.

• Классификатор случайного леса может обрабатывать пропущенные значения. Есть два способа обработки пропущенных значений. Во-первых, использовать медианные значения для замены непрерывных переменных, а во-вторых, вычислить средневзвешенное по близости отсутствующих значений.

• Для выбора признаков можно использовать случайный классификатор леса. Это означает выбор наиболее важных функций из доступных функций набора обучающих данных.

Недостатки алгоритма случайного леса перечислены ниже:

• Самым большим недостатком случайных лесов является их вычислительная сложность. Случайные леса очень медленно делают прогнозы, поскольку для прогнозирования используется большое количество деревьев решений. Все деревья в лесу должны сделать прогноз для одного и того же входного сигнала, а затем провести по нему голосование.

• Модель сложна для интерпретации по сравнению с деревом решений.

Формула итогового классификатора:

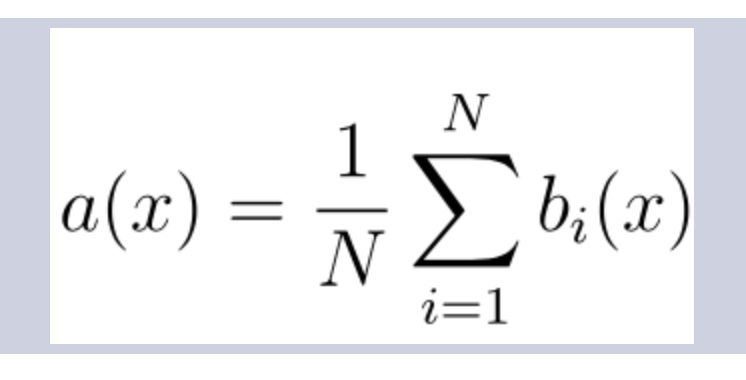
• N – количество деревьев;

• i – счетчик для деревьев;

• b – решающее дерево;

• x – сгенерированная нами на основе данных выборка.

Стоит также отметить, что для задачи классификации мы выбираем решение голосованием по большинству, а в задаче регрессии – средним.

Необходимые параметры алгоритма

Число деревьев – n_estimators

Чем больше деревьев, тем лучше качество, но может сказаться на производительности.

Критерий расщепления – criterion

Также один из самых важных параметров для построения, но без значительной возможности выбора. В библиотеке sklearn для задач классификации реализованы критерии gini и entropy. Они соответствуют классическим критериям расщепления: джини и энтропии.

В свою очередь, для задач регрессии реализованы два критерия (mse и mae), которые являются функциями ошибок Mean Square Error и Mean Absolute Error соответственно. Практически во всех задачах используется критерий mse.

Простой метод перебора поможет выбрать, что использовать для решения конкретной проблемы.

Число признаков для выбора расщепления – max_features

При увеличении max_features увеличивается время построения леса, а деревья становятся похожими друг на друга. В задачах классификации он по умолчанию равен sqrt(n), в задачах регрессии – n/3.

Минимальное число объектов для расщепления – min_samples_split

Второстепенный по своему значению параметр, его можно оставить в состоянии по умолчанию.

Ограничение числа объектов в листьях – min_samples_leaf

Аналогично с min_samples_split, но при увеличении данного параметра качество модели на обучении падает, в то время как время построения модели сокращается.

Максимальная глубина деревьев – max_depth

Чем меньше максимальная глубина, тем быстрее строится и работает алгоритм случайного дерева.

При увеличении глубины резко возрастает качество как на обучении модели, так и на ее тестировании. Если у вас есть возможность и время для построения глубоких деревьев, то рекомендуется использовать максимальное значение данного параметра.

Неглубокие деревья рекомендуется использовать в задачах со значительным количеством шумовых объектов (выбросов)