23. Машина опорных векторов. Для решения каких задач применяется алгоритм? Объясните смысл алгоритма. Понятие гиперплоскости. Напишите наиболее распространенные ядерные функции.

Машины опорных векторов (Support Vector Machine, SVM) широко используется для решения различных задач классификации и регрессии. Он основан на идее поиска оптимальной границы между двумя классами данных, которая максимизирует расстояние до ближайших точек каждого класса.

Смысл алгоритма:

SVM находят гиперплоскость (это многомерная прямая, которая разделяет пространство на две части. В случае двоичной классификации SVM находит гиперплоскость, которая разделяет точки данных двух классов с максимальным отступом (расстоянием). Обобщением понятия плоскости трехмерного пространства на случай n -мерного пространства является понятие гиперплоскости), которая разделяет данные на два класса с максимальным **отступом**. Отступ - это расстояние от гиперплоскости до ближайших точек данных (опорных векторов).

Основная идея метода заключается в отображение векторов пространства признаков, представляющих классифицируемый объекты, в пространство более высокой размерности. Это связано с тем, что в пространстве большей размерности линейная разделимость множества оказывается выше, чем в пространстве меньшей размерности. Причины этого интуитивно понятны: чем больше признаков используется для распознавания объектов, тем выше ожидаемое качество распознавания.

После перевода в пространство большей размерности, в нём строится разделяющая гиперплоскость. При этом все векторы, расположенные с одной «стороны» гиперплоскости, относятся к одному классу, а расположенные с другой — ко второму. Также, по обе стороны основной разделяющей гиперплоскости, параллельно ей и на равном расстоянии от неё строятся две вспомогательные гиперплоскости, расстояние между которыми называют зазор.

Задача заключается в построении разделяющей гиперплоскость таким образом, чтобы максимизировать зазор — область пространства признаков между вспомогательными гиперплоскостями, в которой не должно быть векторов. Предполагается, что разделяющая гиперплоскость, построенная по данному правилу, обеспечит наиболее уверенное разделение классов и минимизирует среднюю ошибку распознавания.

Векторы, которые попадут на границы зазора (т.е. будут лежать на вспомогательных гиперплоскостях), называют опорными векторами

Наиболее распространенные ядерные функции:

Ядерная функция преобразует исходные данные в более высокоразмерное пространство, где их можно разделить линейной гиперплоскостью. Наиболее распространенные ядерные функции:

• Линейная: K(x, y) = x^T * y

• Полиномиальная: K(x, y) = (x^T * y + c)^d

• Радиальная базисная функция (RBF): K(x, y) = exp(-γ ||x - y||^2)

• Гиперболический тангенс: K(x, y) = tanh(α x^T*y + c)

• Т (транспонирование),

• x представляет собой вектор-столбец из n элементов

• y представляет собой вектор-столбец из m элементов

24. Алгоритм решающего дерева. Для решения каких задач применяется алгоритм? Объясните смысл алгоритма. Из чего состоит дерево решений? Формула прироста информации. Напишите формулы для критериев информативности при решении задачи классификации. Какая функция потерь чаще всего используется при решении задачи регрессии.

Алгоритм решающего дерева - это алгоритм машинного обучения, который используется для решения задач классификации и регрессии. Он создает древовидную структуру, которая разветвляется на основе значений признаков в данных.

Основные задачи, которые дерево решений решает в машинном обучении, анализе данных и статистике:

• Классификация — когда нужно отнести объект к конкретной категории, учитывая его признаки.

• Регрессия — использование данных для прогнозирования количественного признака с учетом влияния других признаков.

Смысл алгоритма:

• Решающее дерево — это древовидная структура, где каждый внутренний узел представляет собой признак, а ветви представляют собой возможные значения признака.

• Дерево строится сверху вниз, начиная с корневого узла, который представляет собой весь набор данных.

• На каждом узле алгоритм выбирает лучший признак для разделения данных на основе критерия информативности.

• Разделение продолжается рекурсивно, пока не будут достигнуты узлы-листья, представляющие окончательные предсказания.

Из чего состоит дерево решений:

• Корневой узел: Представляет весь набор данных.

• Внутренние узлы: Представляют признаки, используемые для разделения данных.

• Листья (узлы-листья): Представляют окончательные предсказания или классы.

• Ветви: Представляют возможные значения признаков, используемых для разделения данных.

Формула прироста информации:

Прирост информации измеряет, насколько хорошо условие разделяет данные. Он рассчитывается как разность энтропии данных до и после разделения:

Прирост информации = Энтропия(до) - Энтропия(после)

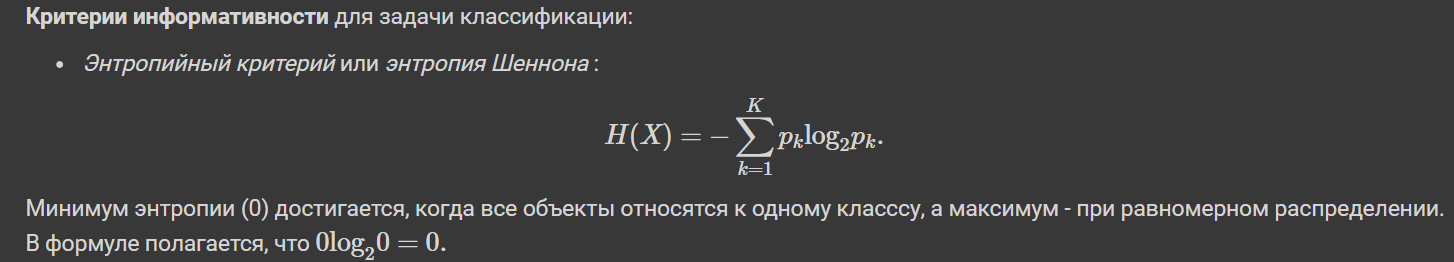
Энтропия - это мера неопределенности в данных. Чем выше энтропия, тем более неопределенны данные. Проще: это то, как много информации, значимой для принятия решения, мы не знаем.

Индекс Джини измеряет вероятность неправильной классификации случайного экземпляра из набора данных. Индекс Джини равен 0, если все экземпляры в наборе данных принадлежат одному классу, и он равен 1, если вероятности всех классов равны. Чем выше индекс Джини, тем более разные данные.

Он рассчитывается как:

Gini(S) = 1 - Σ(p_i)^2

• S: Набор данных

• p_i: Вероятность того, что экземпляр принадлежит к классу i

Индекс нечистоты измеряет степень смешения классов в наборе данных. Индекс нечистоты равен 0, если все экземпляры в наборе данных принадлежат одному классу, и он равен 1, если вероятность наибольшего класса равна 0,5. Чем выше индекс нечистоты, тем более нечистым является набор данных. Он рассчитывается как:

Impurity(S) = 1 - max(p_i)

• S: Набор данных

• p_i: Вероятность того, что экземпляр принадлежит к классу i

При решении задач регрессии в качестве функции потерь используют среднюю квадратическую ошибку (MSE). Это разница между прогнозируемым значением и истинным, возведенная в квадрат и усредненная по всему набору данных. Самая простая функция потерь в задаче классификации — точность (процент правильно угаданных меток).

25. Переобучение решающего дерева. Приведите графический пример переобучения модели. Какой результат точности обучения мы получим для переобученной модели на тестовой и валидационной выборке? Критерии останова для решающего дерева.

Переобучение - ситуация, когда модели машинного обучения показывают отличную эффективность на обучающем наборе данных, но не справляются с новыми, неизвестными данными.

Графический пример переобучения модели:

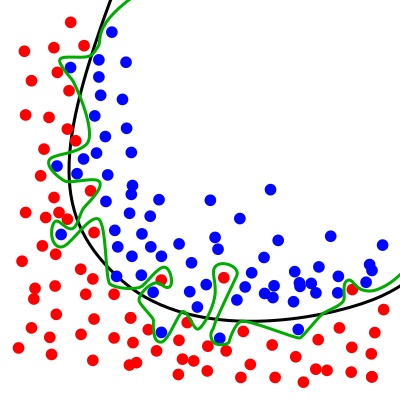
Зелёная разделительная линия показывает переобученную модель, а чёрная линия — регуляризированную модель. Зелёная линия лучше соответствует образцам, по которым проходило обучение, однако классификация по зелёной линии очень зависит от конкретных данных, и скорее всего новые данные будут плохо соответствовать классификации по зелёной линии и лучше — классификации по чёрной линии.

Для переобученной модели точность обучения будет очень высокой, близкой к 100%. Это потому, что модель слишком хорошо подстраивается под обучающие данные и начинает запоминать их особенности и шумы.

Точность на тестовой и валидационной выборке будет низкой по следующим причинам:

• Тестовая выборка - это невиданные данные, которые не использовались для обучения модели. Переобученная модель не может обобщить то, что она выучила на обучающих данных, на новые данные, поэтому ее точность на тестовой выборке будет низкой.

• Валидационная выборка похожа на обучающие данные, но она не использовалась для обучения модели. Хотя точность на валидационной выборке может быть выше, чем на тестовой выборке, она все равно будет ниже, чем точность обучения, поскольку модель все еще переобучена на обучающих данных.

Критерии останова для решающего дерева:

• Ограничение максимальной глубины дерева (Предотвращает переобучение и создание слишком сложных деревьев)

• Ограничение минимального числа объектов в листе (Предотвращает создание слишком маленьких листьев, которые могут быть чувствительны к шумам и выбросам в данных.)

• Ограничение максимального количества листьев в дереве (Контролирует размер и сложность дерева, предотвращая переобучение.)

• Останов в случае, если все объекты в вершине относятся к одному классу (Останавливает создание дерева, когда все экземпляры данных в текущем узле принадлежат одному классу)