17. Параметрические критерии. T-статистика. Напишите определение и формулу для вычисления. Понятие степеней свободы.

Параметрическими называют критерии, которые основаны на предположении, что распределение признака в совокупности подчиняется некоторому известному закону. К таким критериям относятся критерии Стьюдента, Фишера, Пирсона и т.д.

t-статистика - это параметрический критерий, который измеряет, насколько значительна разница между двумя выборочными средними по отношению к изменчивости данных (используется для проверки гипотез о среднем значении генеральной совокупности при неизвестной дисперсии). Это стандартный инструмент для оценки гипотез о значимости различий между выборками.

Формула для вычисления t-статистики:

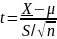
где X - выборочное среднее

μ - гипотетическое среднее

S - выборочное стандартное отклонение

n - размер выборки.

Степени свободы - это число независимых наблюдений в выборке, которые могут свободно изменяться (и говорят вам, сколько элементов может быть выбрано случайным образом, прежде чем должны быть введены ограничения). В t-статистике степени свободы равны n - 1, где n - размер выборки. Они используются для определения критического значения t-статистики и расчета p-значения.

Пример определения степеней свободы:

Рассмотрим выборку данных, состоящую из пяти натуральных чисел. Значения пяти целых чисел должны иметь среднее значение шесть. Если четыре элемента в наборе данных равны {3, 8, 5, 4}, пятое число должно быть 10. Поскольку первые четыре числа могут быть выбраны случайным образом, степень свободы равна четырем.

18. Одновыборочный и парный t-тест. Объяснить разницу. Придумать пример на тестирование гипотезы одним из тестов, вычислить t-наблюдаемое.

Одновыборочный t-тест используется для проверки гипотезы о среднем значении генеральной совокупности, когда известна ее дисперсия. Парный t-тест используется для сравнения двух средних значений, полученных из двух связанных выборок.

Чтобы было понятнее:

Одновыборочный - При выполнении этого теста среднее или среднее значение одной группы сравнивается с установленным средним значением, которое является либо теоретическим значением, либо средним значением для населения. Например, учитель хочет определить средний рост учеников 5-го класса и сравнить его с установленным значением более 45 кг.

Парный - Эта проверка гипотезы проводится, когда две группы принадлежат к одной и той же популяции или группе. Группы изучаются либо в два разных времени, либо в двух различных условиях.

Пример для одновыборочного t-теста: предположим, что средний вес яблок в магазине должен быть не менее 150 граммов. Взяв выборку из 20 яблок, мы получили средний вес 145 граммов и выборочное стандартное отклонение 10 граммов. Вычисляем t-наблюдаемое: t = (145 - 150) / (10 / √20) = -2.24. Если уровень значимости α = 0.05 (типичное значение по условие) и степени свободы 19 (20-1), то критическое значение t-статистики (табличка сделанная математиками, где значения, определяемые по уровню значимости и степеням свободы) равно ±2.093. Так как t-наблюдаемое меньше критического значения, мы отвергаем гипотезу о среднем весе яблок в магазине не менее 150 граммов.

Уровень значимости статистического теста – это вероятность отклонить нулевую гипотезу, когда на самом деле она верна.

19. Линейная регрессия. Нахождение уравнения регрессии. Напишите формулу для поиска коэффициентов линейного уравнения. Приведите практический пример и постройте график уравнения регрессии по собственным данным.

Линейная регрессия - это метод машинного обучения, который используется для построения модели, которая описывает линейную зависимость между входными признаками и выходными значениями.

y = a + bx

* y - зависимая переменная

* x - независимая переменная

* a - отрезок на оси ординат (значение y при x = 0)

* b - угловой коэффициент (наклон линии)

X	Y	X-Mx	Y-My	(X-Mx)2	(X-Mx)(Y-My)
3	6	-1	-1	1	1
5	9	1	2	1	2
1	3	-3	-4	9	12
7	10	3	3	9	9
Mx=4	My=7			Sum=20	Sum=24

Если что M – это среднее арифмическое (вроде очевидно, но мало ли что очевидно…)

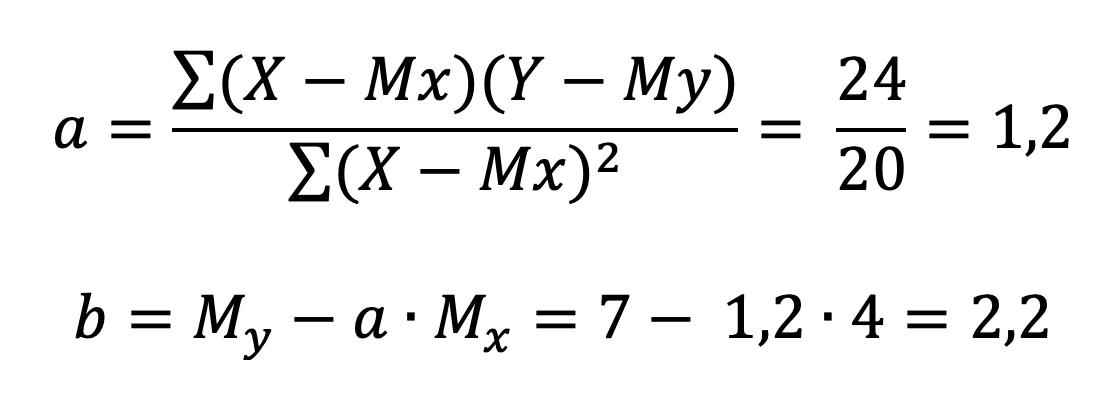
Собираем наш конструктор и получаем

Для построения графика линейной регрессии нужно провести график прямой из получившегося уравнения, а потом проставить точки на графике из имеющихся данных

В нашем случае получается:

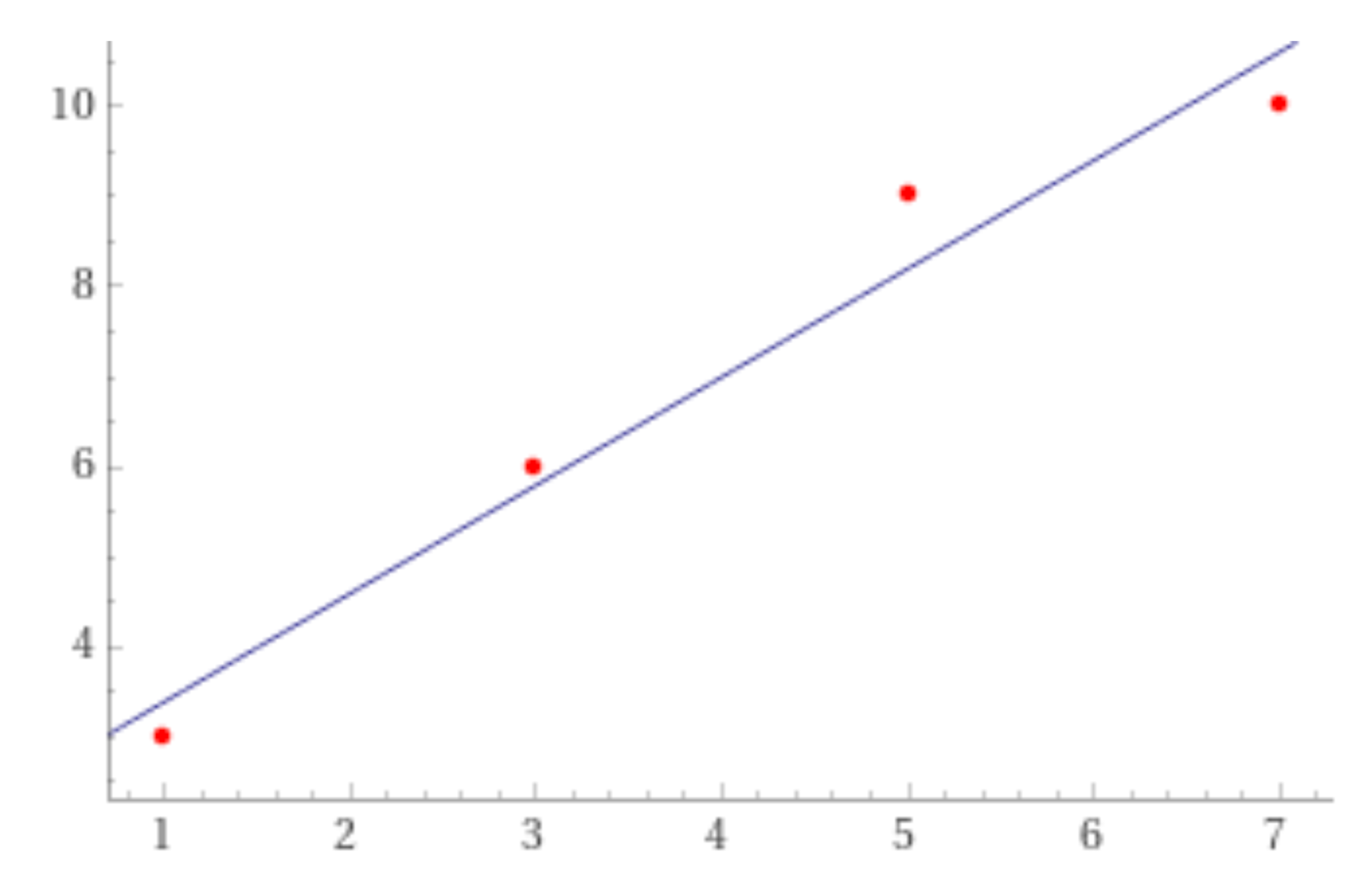
20. Оценка качества регрессии. Использование среднеквадратической ошибки. Для чего используется коэффициент детерминации R²? Приведите практический пример и найдите коэффициент детерминации для собственных данных. Сделайте вывод о разбросе данных

Для оценки качества регрессии используются различные метрики. Две из наиболее распространенных метрик - это среднеквадратическая ошибка (MSE) и коэффициент детерминации (R2).

MSE (Mean squared error) – метрика измеряет, насколько хорошо модель регрессии предсказывает значения зависимой переменной. Чем меньше значение MSE, тем лучше модель соответствует данным. MSE рассчитывается как средняя квадратичная разность между фактическими значениями и предсказанными значениями.

Простыми словами: MSE показывает, насколько предсказанные значения модели отличаются от фактических значений.

Из вопроса 20 возьмем данные и рассчитанное уравнение

Пример для первой строки

X	Y
3	6	5,8	-0,2	0,04
5	9	8,2	-0,8	0,64
1	3	3,4	0,4	0,16
7	10	10,6	0,6	0,36

Теперь считаем ср. арифм. последнего столбца

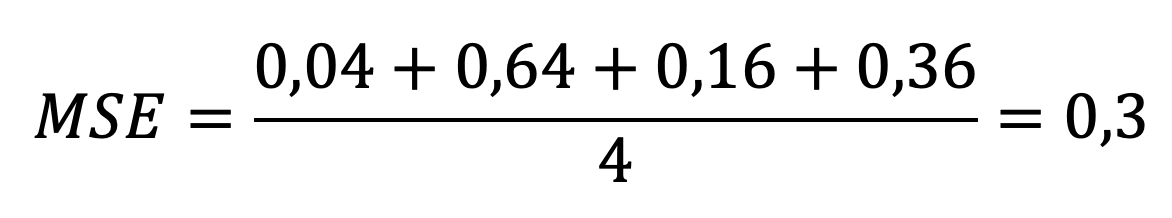
Коэффициент детерминации (R²) отражает, какой процент разброса данных мы можем объяснить нашей моделью.

Простыми словами: R2 показывает, насколько хорошо модель регрессии описывает данные. Высокое значение R2 означает, что модель хорошо улавливает тренд в данных, а низкое значение R2 означает, что модель не очень хорошо улавливает тренд.

Для того, чтобы рассчитать коэффициент детерминации, необходимо найти отклонения от среднего для целевой переменной и отклонения от среднего для предсказания целевой переменной. И после этого разделить первый результат в квадрате на второй результат в квадрате.

X	Y		Y-My		(Y-My)2
3	6	5,8	-1	-1,2	1	1,44
5	9	8,2	2	1,2	4	1,44
1	3	3,4	-4	-3,6	16	12,96
7	10	10,6	3	3,6	9	12,96
	My=7				Sum=30	Sum=28,36

Это означает, что мы можем объяснить с помощью нашего уравнения 94,5% данных

21. Логистическая регрессия. Для решения каких задач применяется алгоритм? Напишите определение шанса. Выведите логистическую функцию, постройте её график. Приведите пример нахождения оценки вероятности для своего линейного уравнения.

Логистическая регрессия — это алгоритм машинного обучения, который используется для прогнозирования. Логистическая регрессия используется для решения задач бинарной классификации, то есть разделения объектов на два класса (например, "да" или "нет", "истина" или "ложь", "заболевание" или "здоровье" и т.д.). Примеры задач, где используется логистическая регрессия, включают определение того, является ли электронное письмо спамом или не спамом, определение того, будет ли клиент покупать определенный продукт, или нет, и так далее.

Шанс - это отношение вероятности события к вероятности его невозникновения. Например, если вероятность того, что команда выиграет матч, равна 0,8, то шансы на победу будут равны 0,8 / 0,2 = 4. То есть, шансы на победу в матче для команды равны 4 к 1.

Логистическая функция, также называемая сигмоидой, определяет вероятность отнесения объекта к одному из двух классов в зависимости от значения линейной комбинации его признаков (суём в функцию число и получаем вероятность от 0 до 1 (0 - объект не принадлежит классу, 1 - объект принадлежит классу)), чтобы ее вывести, вернемся к шансу. Запишем формулу шанса наступления события

Чтобы получить вероятность p, мы решаем это уравнение относительно p:

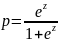
После простых алгебраических преобразований мы можем записать это выражение в виде логистической функции:

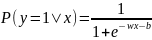
где w - вектор весов

x - вектор признаков

b - свободный член.

График этой функции выглядит как S-образная кривая, которая изменяется от 0 до 1:

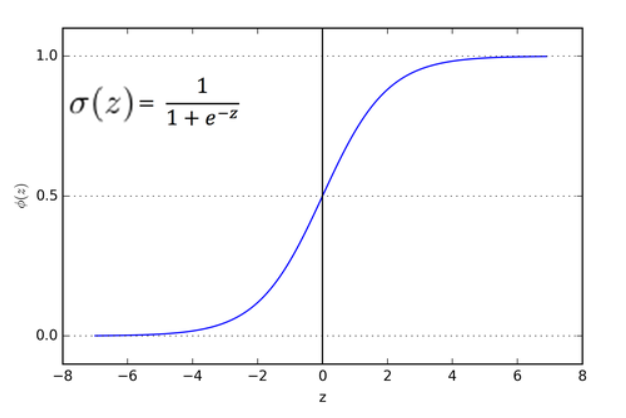
Для нахождения оценки вероятности для своего линейного уравнения необходимо подставить его в логистическую функцию и вычислить значение. Например, если линейное уравнение имеет вид y = 2x + 1, то соответствующее уравнение для логистической регрессии будет выглядеть следующим образом:

Подставляя значения признаков, можно вычислить вероятность отнесения объекта к классу 1.

22. Алгоритм Naïve Bayes. Для решения каких задач применяется алгоритм? Сформулируйте формулу теоремы Байеса. Объясните смысл составных частей. Почему алгоритм называется «наивным»? Приведите практический пример применения алгоритма Naïve Bayes для задачи фильтрации СПАМ-сообщений.

Алгоритм Naïve Bayes - это классификатор, который используется для прогнозирования вероятности принадлежности объекта к определенному классу на основе его признаков. Он применяется в следующих задачах:

• Фильтрация спама

• Распознавание текстов

• Медицинская диагностика

• Анализ финансовых данных

Теорема Байеса - это математическая формула, которая описывает вероятность наступления события A при условии наступления события B:

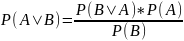
• P(A|B) - вероятность того, что событие A произойдет при условии, что событие B произошло;

• P(B|A) – условная вероятность того, что событие B произойдет при условии, что событие A произошло;

• P(A) и P(B) - априорные вероятности событий A и B.

Смысл составных частей

• P(A|B): условная вероятность события A при условии B (например, вероятность того, что электронное письмо является спамом при условии наличия определенных слов)

• P(B|A): условная вероятность события B при условии A (например, вероятность наличия определенных слов в спам-сообщении)

• P(A): априорная вероятность события A (например, вероятность того, что электронное письмо является спамом)

• P(B): вероятность события B (например, вероятность наличия определенных слов в любом электронном письме)

Суть теоремы Байеса заключается в том, что она позволяет пересчитывать вероятности на основе новой информации. Например, если мы знаем вероятность заболевания определенной болезнью, то мы можем использовать теорему Байеса, чтобы вычислить вероятность заболевания при наличии некоторых симптомов.

Алгоритм Naïve Bayes является «наивным», потому что он предполагает, что все признаки независимы друг от друга. То есть, например, в задаче классификации текстов он предполагает, что появление каждого слова не зависит от появления других слов в тексте. Это, конечно, не всегда верно, но на практике такой подход часто работает достаточно хорошо и дает высокую скорость обучения и классификации.

Преимущества:

• Высокая точность

• Малое количество обучающих данных

• Быстрая обучаемость и выполнение

Недостатки:

• Чувствительность к шуму в данных (неинформативные или дублирующие признаки)

• Может плохо работать при больших объемах размерных данных (проклятие размерности)

• Предположение о независимости признаков может быть неверным на практике

Пример: Фильтрация спама

P(Спам|Текст) = (P(Текст|Спам) * P(Спам)) / P(Текст)

Составные части:

• P(Текст|Спам): вероятность наличия конкретного текста в спам-сообщении (например, фраза «купить Виагру»)

• P(Спам): априорная вероятность того, что электронное письмо является спамом

• P(Текст): вероятность наличия конкретного текста в любом электронном письме

В задаче фильтрации СПАМ-сообщений мы можем использовать алгоритм Naïve Bayes для определения, является ли сообщение СПАМом или нет. Для этого мы обучаем модель на наборе текстовых данных, которые размечены как СПАМ или не СПАМ, и вычисляем априорные вероятности для каждого класса. Затем мы извлекаем признаки из нового сообщения, например, количество вхождений определенных слов, и используем модель, чтобы вычислить вероятности для каждого класса. Например, если вероятность, что сообщение является СПАМом, больше, чем вероятность, что оно не является СПАМом, то мы классифицируем его как СПАМ.