8. Уравнение регрессии

8.1Линейная регрессия

Пусть наблюдаемая случайная величина Y зависит от случайной величины X. Обозначим через f(x); функцию задающую зависимость среднего значения Y от значений X

M(Y=X = x) = f(x):

Уравнение y = f(x) называется уравнением регрессии.

Проведем n экспериментов, в результате которых случайная величина X примет последовательно значения x1; x2; . . . , xn; и получим соответствующие значения случайной величины Y : y1; y2; . . . , yn: Обозначим разницу между yi и ее математическим ожиданием

i = yi M(Y=X = xi) = yi f(xi):

Обычно предполагают, что i – независимы и распределены нормально с параметрами 0, 2: Требуется по значениям x1; . . . , xn и y1; . . . , yn оценить как можно точнее функцию f(x): Сначала заранее определяют вид функции f(x): Будем предполагать, что f(x) – линейная функция

f(x) = ax + b:

Оценки неизвестных параметров a и b находят с помощью метода максимального правдоподобия или метода наименьших квадратов, суть которого мы рассмотрим позже. Эти оценки выглядят следующим образом:

(Y )

a = (X)r; b = M(Y ) rM(X) (X):

Прямая

y = M(Y ) + r (X)(x M(X))

называется прямой среднеквадратической регрессии Y на X. Величина = 2(Y )(1 r2) называется остаточной дисперсией

Y на X. Она определяет величину ошибки приближенного равенства

74

Y aX + b. Если r = 1, то ошибка равна нулю, а величины Y и X связаны линейной функциональной зависимостью.

Заменяя M(X); M(Y ); (X); (Y ) и r на их точечные оценки, получаем уравнение выборочной прямой среднеквадратической регрессии Y на X:

s0(Y )

y = Y + rB s0(X)(x X):

Аналогично получается уравнение выборочной прямой среднеквадратической регрессии X на Y :

x = X + rB s0(Y )(y Y ):

8.2 Нелинейная регрессия

Рассмотрим общую постановку задачи регрессионного анализа.

Пусть имеется выборка (x; y) = ((x1; y1); (x2; y2); : : : ; (xn; yn)) из распределения случайной величины (X; Y ). И пусть известно, что случайные величины X и Y зависимы. Важное прикладное значение имеет задача о представлении одной из этих величин как функции от другой.

Проведение регрессионного анализа можно разделить на три этапа: выбор формы зависимости (типа уравнения), вычисление параметров выбранного уравнения, оценка достоверности полученного уравнения.

Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, наблюдений расположения точек (xi; yi) на плоскости и т.д.

Обозначим через f(x; ); функцию задающую зависимость среднего значения Y от значений X (здесь = ( 1; : : : ; k) - вектор параметров):

M(Y=X = x) = f(x; ):

Уравнение y = f(x; ) называется уравнением регрессии.

Для определения неизвестных параметров 1; : : : ; k можно использовать метод наименьших квадратов.

Суть этого метода состоит в том, что наилучшим считается такое положение линии регрессии, при котором сумма квадратов отклонений значений f(xi; ) от соответствующих yi минимальна. Метод состоит в минимизации функции

n

X

Q( ) = (yi f(xi; ))2:

i=1

75

8.3Построение уравнения нелинейной регрессии в Mathcad.

Пусть экспериментально получены следующие значения x и y:

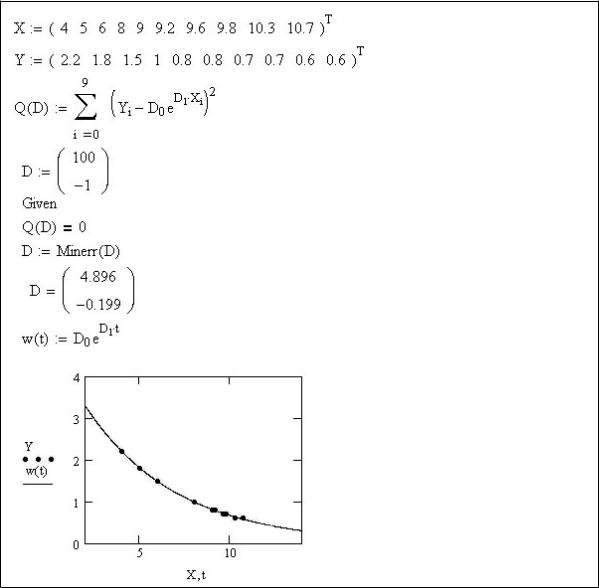
Считая справедливой зависимость y(x; D) = D0eD1x, находим неизвестные параметры D0 и D1 c помощью метода наименьших квадратов. В результате получаем уравнение регрессии y = 4:896e 0:199x:

Вводятся элементы выборки (X; Y )

Задается минимизирующая функция Q(D)

Находится вектор параметров D, при котором Q(D) достигает минимального значения.

Полученное уравнение регрессии.

На графике отображены исходные данные и линия регрессии, соответствующая полученному уравнению.

Рис. 8.1. Построение уравнения регрессии с помощью метода наименьших квадратов

76

Текст программы, реализующей построение уравнения регрессии приведен на рис. 8.1. В данной программе для минимизации функции Q(D) используется встроенная функция Minerr(). Однако минимизацию можно провести известным методом исследования функции нескольких переменных на экстремум с помощью дифференциального исчисления.

8.4Задание к лабораторной работе

1. В табл. 8.1 находятся выборка (x; y) из двумерного нормального распределения случайной величины (X; Y ). Первый столбец матрицы - значения x, второй столбец - соответствующие значения y.

На плоскости Oxy нанести элементы выборки (x; y) и построить прямую среднеквадратической регресcии Y на X, определить остаточную дисперсию Y на X. Сделать вывод о правомерности описания зависимости Y (X) линейной функцией.

2. В таблице 8.2 находится выборка (x; y).

С помощью метода наименьших квадратов построить уравнения регрессии, считая справедливыми следующие формы зависимости y от x:

а) y = a sin (bx), б) y = loga bx + c, в) y = a0 + a1x + a2x2. (Поиск минимума функции Q(D) проводить, исследуя эту функцию

на экстремум с помощью частных производных).

На одном графике изобразить исходные данные и полученные линии регрессии. Сделать вывод о том, какая из функций наилучшим образом представляет зависимость y от x.

77

Таблица 8.2.

Вариант 1

81

Вариант 14

82