Исследование_Операций_ЛР4

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н. Н. Григорьева
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №4

РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ МАТРИЧНЫХ ИГР

по курсу: ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы:

Изучить базовые сведения о задачах об антагонистических играх и таких методах их решения как аналитический, графический, понятие равновесия по Нешу, привидение к задаче линейного программирования.

Индивидуальное задание (Вариант 9):

1. Проанализировать матрицу игры, определить, имеет ли игра решение в чистых стратегиях, цену игры (или нижнюю и верхнюю цены игры).

2. Найти решение в смешанных стратегиях матричной игры 2×2 аналитически и с использованием понятия равновесия по Нэшу.

3. Провести сокращение размерности матрицы игры до формата m×2 или 2×n и найти ее решение в смешанных стратегиях графическим методом.

4. Представить задачу в виде задачи линейного программирования и решить ее с помощью MS Excel. Сравнить результаты, полученные в пунктах 3 и 4.

Данные для заданий приведены на Рисунке 1.

Рисунок 1 – Данные по задачам, вариант № 9

Ход работы:

1. Проанализирована матрица игры : ;

Минимальный выигрыш для игрока A: , нижняя цена α = 1;

Максимальный проигрыш для игрока B: , верхняя цена β = 1;

Тогда α = β → игра имеет седловую точку и два решения в чистых стратегиях: равновесные пары стратегий (А1 , В2) и (А3 , В2). Цена игры = 1.

2. Аналитический поиск решения в смешанных стратегиях матричной игры 2x2:

Дана матрица игры минимальной размерности:

Нижняя граница = 0.6; Верхняя граница = 0.8;

Можно определять вероятность одной из двух стратегий, так как:

При использовании оптимальных стратегий составлена система:

Тогда вероятности использования смешанных стратегий игрока A (x1;x2):

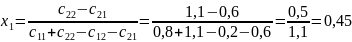
Вероятности использования смешанных стратегий игрока B (y1;y2):

Цену игры можно определить как:

Далее данная задача была решена с помощью использования понятия равновесия по Нешу.

Математическое ожидание выигрыша игрока А можно определить как:

При достижении равновесия

При использовании оптимальных стратегий достигается так равновесие по Нэшу - экстремум функции относительно всех ее переменных:

Математическое ожидание выигрыша игрока А:

Координаты точки Неша:

Тогда цена игры в точке равновесия по Нешу:

Полученные результаты совпали с результатами найденными аналитическим методом. Ответ: x1= 0,45; x2 = 0,55; y1 = 0,82; y2 = 0,18. Цена игры = 0,69.

3. Для сокращения размерности матрицы рассматриваются её выигрышные и проигрышные стратегии.

Для игрока A стратегия 3 уступает стратегии 1, поэтому от неё можно избавиться (Таблицы 1).

	B1	B2	B3	B4	B5
A1	3,0	3,8	2,6	5,0	5,8
A2	5,4	4,2	4,6	3,0	2,6
A3	1,4	3,4	2,2	1,0	5,4

Таблица 1 – Поиск невыгодных стратегий для игрока A

Для игрока B стратегия 1 дает большие проигрыши чем стратегия 3, поэтому оставляем стратегии 2,3,4 и 5 (Таблица 2).

	B1	B2	B3	B4	B5
A1	3,0	3,8	2,6	5,0	5,8
A2	5,4	4,2	4,6	3,0	2,6

Таблица 2 – Поиск невыгодных стратегий для игрока B

Матрица сокращена до размерности 2x4. Оставшиеся стратегии приведены в Таблице 3.

	B2	B3	B4	B5
A1	3,8	2,6	5,0	5,8
A2	4,2	4,6	3,0	2,6

Таблица 3 – Оставшиеся стратегии

Нижняя цена игры α = 2.6; Верхняя цена игры β = 4.2;

В соответствии с Рисунком 2, проведен поиск решения в смешанных стратегиях графическим методом.

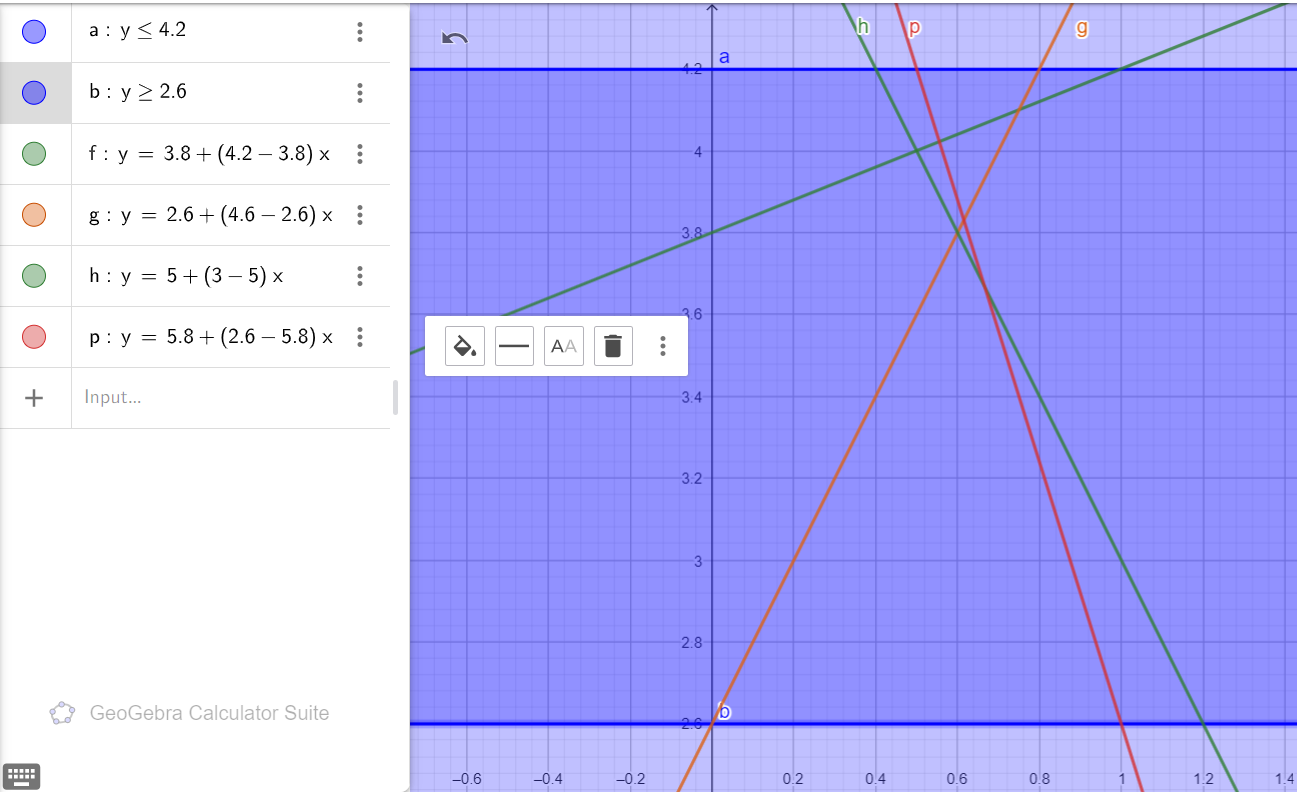
Рисунок 2 – График решений

Максимальная оптимальная стратегия для игрока А – точка пересечения функций g и h, так как их задают минимальные стратегии выигрыша игрока B: B2 (2.6) и B3 (3.0). Высота точки пересечения соответствует цене игры: v = 3.8. Для x значение в точке пересечения:

Тогда оптимальные частоты стратегий игрока A: 0,6 и 1-0.6 = 0.4. Зная цену игры и оптимальную стратегию первого игрока определены оптимальные частоты активных стратегий второго игрока:

В данном случае стратегия B1, B4 не рассматривается, так как дает больший проигрыш второму игроку.

Ответ: цена игры = 3.8; Стратегии игроков: (0.5, 0, 0.5, 0), (0.4, 0.6).

4. Задача представлена в виде задачи линейного программирования и решена в программе Excel при помощи инструмента поиск решений. Результат решения представлен на Рисунках 3-4.

В результате была найдена цена игры, соответствующая найденному значению графическим методом. Параметры поиска решений в Excel представлены на Рисунках 4 и 6.

Рисунок 3 – Таблица для поиска решений с результатами игрока А

Рисунок 4 – Параметры поиска решений

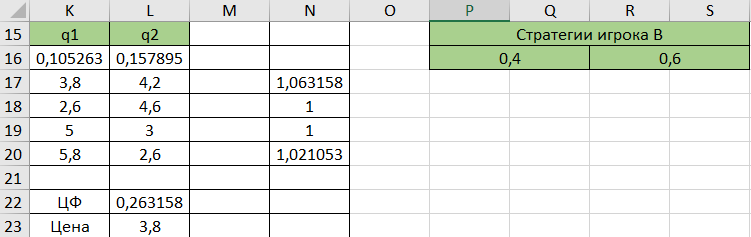
Рисунок 5 - Таблица для поиска решений с результатами игрока B

Рисунок 6 – Параметры поиска решений (Игрок B)

Вывод:

В ходе выполнения лабораторной работы изучены базовые сведения о задачах об антагонистических играх и такие методы их решения как аналитический, графический, использование понятия равновесия по Нешу, привидение к задаче линейного программирования.

В результате решено 3 задачи с использованием различных методов. Наиболее удобным способом оказалось решение задачи линейного программирования с помощью средств компьютера, так как результаты можно считать надежными и программа может обработать задачи с большим количеством данных быстрее и эффективнее человека.