
Исследование_Операций_ЛР3
.docxГУАП
КАФЕДРА № 41
ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ
ПРЕПОДАВАТЕЛЬ
Старший преподаватель |
|
|
|
Н. Н. Григорьева |
должность, уч. степень, звание |
|
подпись, дата |
|
инициалы, фамилия |
ОТЧЕТ О ПРАКТИЧЕСКОЙ РАБОТЕ №3 |
РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ БЕЗ ОГРАНИЧЕНИЙ И С ОГРАНИЧЕНИЯМИ. |
по курсу: ИССЛЕДОВАНИЕ ОПЕРАЦИЙ |
|
|
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. № |
4117 |
|
|
|
|
|
|
|
подпись, дата |
|
инициалы, фамилия |
Санкт-Петербург 2024
Цель работы:
Получение практических навыков решения задач при помощи динамического программирования.
Индивидуальное задание вариант 9:
Задание 1: решить задачу эвакуации при заданном ограничении на грузоподъемность G. Каждый из предметов – в единственном числе. Условия приведена на Рисунке 1.

Рисунок 1 – Условия первой задачи
Задание 2: решить задачу о распределении ресурсов по таблице исходных данных, представленной на Рисунке 2.
Ход работы:
Задание 1:
По задаче нужно определить, какие предметы нужно взять, чтобы получить с них наибольшую стоимость W, не превысив максимальной грузоподъемности G в 11 единиц:
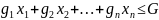
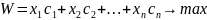
Для решения было принято использовать программу MS Excel. В Таблице 1.1 приведены исходные данные с весом и ценами предметов.
Таблица 1.1 – Исходные условия
|
П1 |
П2 |
П3 |
П4 |
П5 |
g (вес) |
2 |
4 |
4 |
6 |
7 |
C (цена) |
30 |
40 |
45 |
50 |
60 |
Для решения постепенно заполняется Таблица 1.2, в которой исходя из доступного для взятия веса определяется какие ресурсы брать (1) или нет (0). Таблица заполняется снизу вверх. В данном случае задача разбивается этапы, на каждом из которых рассматривается взятие конкретного предмета.
Вначале до S = 7 рассматривается взятие 5-го предмета, так как он весит 7 и является самым дорогим. Четвертый предмет, весом в 6, рассматривается при S = 6, так как первый и самый дорогой предмет превышает данный вес.
При S1 = 10 и 11, можно рассмотреть также взятие 3-го предмета, так как его вес <= S – 7, а стоимость больше, чем у предметов с тем же весом или меньше. Для этого выполняются вспомогательные расчеты, приведенные в Таблице 1.3, где для S = 10 и 11 w3 находится равным 95 и 105.
Аналогичным образом строятся таблицы для рассмотрения взятия 2-го и 1-го предметов, из которых в итоговую таблицу выписываются максимальные возможные стоимости на выбранном этапе. В конечном счете для S1 – начального состояния при котором доступно 11 единиц веса, рассматривается взятие 1-го предмета исходя из ранее полученных выручек при рассмотрении предыдущего состояния. Для данной задачи получается, что максимальная стоимость предметов, которые можно взять при ограничении по весу в 11 единиц составляет 115. Для этого нужно выбрать 1,2 и 3 предметы. Итоговое решение представлено в Таблице 1.6.
Таблица 1.2 – Итоговый расчет
S |
П5 |
П4 |
П3 |
П2 |
П1 |
|||||
x5 |
C5 |
x4 |
w4 |
x3 |
w3 |
x2 |
w2 |
x1 |
w1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
4 |
0 |
0 |
0 |
0 |
1 |
45 |
0 |
45 |
|
|
5 |
0 |
0 |
0 |
0 |
1 |
45 |
0 |
45 |
|
|
6 |
0 |
0 |
1 |
50 |
0 |
50 |
0 |
50 |
|
|
7 |
1 |
60 |
0 |
60 |
0 |
60 |
0 |
60 |
|
|
8 |
1 |
60 |
0 |
60 |
0 |
60 |
1 |
85 |
|
|
9 |
1 |
60 |
0 |
60 |
0 |
60 |
1 |
85 |
|
|
10 |
1 |
60 |
0 |
60 |
1 |
95 |
1 |
95 |
|
|
11 |
1 |
60 |
0 |
60 |
1 |
105 |
0 |
105 |
1 |
115 |
Таблица 1.3 – Вспомогательные расчеты для S3
S3 |
x3 |
c3x3 |
S4 |
w4 |
w3=c3x3+w4 |
10 |
0 |
0 |
10 |
60 |
60 |
1 |
45 |
6 |
50 |
95 |
|
11 |
0 |
0 |
11 |
60 |
60 |
1 |
45 |
7 |
60 |
105 |
Таблица 1.4 – Вспомогательные расчеты для S2
S2 |
x2 |
c2x2 |
S3 |
w3 |
w2=C2X2+w3 |
8 |
0 |
0 |
8 |
60 |
60 |
1 |
40 |
4 |
45 |
85 |
|
9 |
0 |
0 |
9 |
60 |
60 |
1 |
40 |
5 |
45 |
85 |
|
10 |
0 |
0 |
10 |
95 |
95 |
1 |
40 |
6 |
50 |
90 |
|
11 |
0 |
0 |
11 |
105 |
105 |
1 |
40 |
7 |
60 |
100 |
Таблица 1.5 – Вспомогательные расчеты для S1
S1 |
x1 |
c1x1 |
S2 |
w2 |
w1 |
11 |
0 |
0 |
11 |
105 |
105 |
1 |
30 |
9 |
85 |
115 |
Таблица 1.6 – Итоговое решение
|
П1 |
П2 |
П3 |
П4 |
П5 |
g (вес) |
2 |
4 |
4 |
6 |
7 |
C (цена) |
30 |
40 |
45 |
50 |
60 |
x |
1 |
1 |
1 |
0 |
0 |
Задание 2:
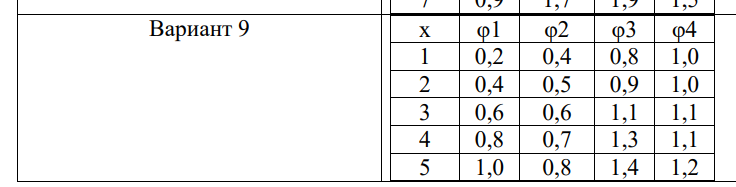
Вторая задача решается аналогичным образом, только на каждом этапе решения больше вариантов, так как для каждого рассматриваемого предприятия можно выделять разное количество ресурсов, от чего изменяется его выручка. В Таблице 2.1 приведены исходные данные по задаче: всего рассматривается 4 предприятия и ограниченным количеством ресурсов в 8 единиц.
Для состояний S3-S1 составлены вспомогательные таблицы, с поиском лучшей прибыли при каждом варианте выделенных ресурсов (от 0 до 8). При этом для S1 сразу рассматривается вариант для максимума доступных ресурсов, так как это исходное состояние. Расчеты приведены в Таблицах 2.2 – 2.4
Постепенно с записью вспомогательных таблиц по этапам, заполняется сводная Таблица 2.5, по которой в конце можно определить распределение ресурсов исходя из найденной максимальной выручки. Для данной задачи, в соответствии с Таблицей 2.6, результат распределения следующий: 5 ресурсов для первого предприятия и по 1 для оставшихся трёх, с общей выручкой в 3.2.
Таблица 2.1 – Исходные условия
X |
φ1 |
φ2 |
φ3 |
φ4 |
1 |
0,2 |
0,4 |
0,8 |
1 |
2 |
0,4 |
0,5 |
0,9 |
1 |
3 |
0,6 |
0,6 |
1,1 |
1,1 |
4 |
0,8 |
0,7 |
1,3 |
1,1 |
5 |
1 |
0,8 |
1,4 |
1,2 |
6 |
1,2 |
0,9 |
1,5 |
1,2 |
7 |
1,4 |
1 |
1,5 |
1,3 |
8 |
1,5 |
1,1 |
1,6 |
1,3 |
Таблица 2.2 – Вспомогательные расчеты для S3
S3 |
x3 |
φ3 |
S4 |
φ4 |
w3=φ3+φ4 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0,8 |
0 |
0 |
0,8 |
|
2 |
0 |
0 |
2 |
1 |
1 |
1 |
0,8 |
1 |
1 |
1,8 |
|
2 |
0,9 |
0 |
0 |
0,9 |
|
3 |
0 |
0 |
3 |
1,1 |
1,1 |
1 |
0,8 |
2 |
1 |
1,8 |
|
2 |
0,9 |
1 |
1 |
1,9 |
|
3 |
1,1 |
0 |
0 |
1,1 |
|
4 |
0 |
0 |
4 |
1,1 |
1,1 |
1 |
0,8 |
3 |
1,1 |
1,9 |
|
2 |
0,9 |
2 |
1 |
1,9 |
|
3 |
1,1 |
1 |
1 |
2,1 |
|
4 |
1,3 |
0 |
0 |
1,3 |
|
5 |
0 |
0 |
5 |
1,2 |
1,2 |
1 |
0,8 |
4 |
1,1 |
1,9 |
|
2 |
0,9 |
3 |
1,1 |
2 |
|
3 |
1,1 |
2 |
1 |
2,1 |
|
4 |
1,3 |
1 |
1 |
2,3 |
|
5 |
1,4 |
0 |
0 |
1,4 |
|
6 |
0 |
0 |
6 |
1,2 |
1,2 |
1 |
0,8 |
5 |
1,2 |
2 |
|
2 |
0,9 |
4 |
1,1 |
2 |
|
3 |
1,1 |
3 |
1,1 |
2,2 |
|
4 |
1,3 |
2 |
1 |
2,3 |
|
5 |
1,4 |
1 |
1 |
2,4 |
|
6 |
1,5 |
0 |
0 |
1,5 |
|
7 |
0 |
0 |
7 |
1,3 |
1,3 |
1 |
0,8 |
6 |
1,2 |
2 |
|
2 |
0,9 |
5 |
1,2 |
2,1 |
|
3 |
1,1 |
4 |
1,1 |
2,2 |
|
4 |
1,3 |
3 |
1,1 |
2,4 |
|
5 |
1,4 |
2 |
1 |
2,4 |
|
6 |
1,5 |
1 |
1 |
2,5 |
|
7 |
1,5 |
0 |
0 |
1,5 |
|
8 |
0 |
0 |
8 |
1,3 |
1,3 |
1 |
0,8 |
7 |
1,3 |
2,1 |
|
2 |
0,9 |
6 |
1,2 |
2,1 |
|
3 |
1,1 |
5 |
1,2 |
2,3 |
|
4 |
1,3 |
4 |
1,1 |
2,4 |
|
5 |
1,4 |
3 |
1,1 |
2,5 |
|
6 |
1,5 |
2 |
1 |
2,5 |
|
7 |
1,5 |
1 |
1 |
2,5 |
|
8 |
1,6 |
0 |
0 |
1,6 |
Таблица 2.3 – Вспомогательные расчеты для S2
S2 |
x2 |
φ2 |
S3 |
w3 |
w2=φ2+φ3 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0,4 |
0 |
0 |
0,4 |
|
2 |
0 |
0 |
2 |
1,8 |
1,8 |
1 |
0,4 |
1 |
1 |
1,4 |
|
2 |
0,5 |
0 |
0 |
0,5 |
|
3 |
0 |
0 |
3 |
1,9 |
1,9 |
1 |
0,4 |
2 |
1,8 |
2,2 |
|
2 |
0,5 |
1 |
1 |
1,5 |
|
3 |
0,6 |
0 |
0 |
0,6 |
|
4 |
0 |
0 |
4 |
2,1 |
2,1 |
1 |
0,4 |
3 |
1,9 |
2,3 |
|
2 |
0,5 |
2 |
1,8 |
2,3 |
|
3 |
0,6 |
1 |
1 |
1,6 |
|
4 |
0,7 |
0 |
0 |
0,7 |
|
5 |
0 |
0 |
5 |
2,3 |
2,3 |
1 |
0,4 |
4 |
2,1 |
2,5 |
|
2 |
0,5 |
3 |
1,9 |
2,4 |
|
3 |
0,6 |
2 |
1,8 |
2,4 |
|
4 |
0,7 |
1 |
1 |
1,7 |
|
5 |
0,8 |
0 |
0 |
0,8 |
|
6 |
0 |
0 |
6 |
2,4 |
2,4 |
1 |
0,4 |
5 |
2,3 |
2,7 |
|
2 |
0,5 |
4 |
2,1 |
2,6 |
|
3 |
0,6 |
3 |
1,9 |
2,5 |
|
4 |
0,7 |
2 |
1,8 |
2,5 |
|
5 |
0,8 |
1 |
1 |
1,8 |
|
6 |
0,9 |
0 |
0 |
0,9 |
|
7 |
0 |
0 |
7 |
2,5 |
2,5 |
1 |
0,4 |
6 |
2,4 |
2,8 |
|
2 |
0,5 |
5 |
2,3 |
2,8 |
|
3 |
0,6 |
4 |
2,1 |
2,7 |
|
4 |
0,7 |
3 |
1,9 |
2,6 |
|
5 |
0,8 |
2 |
1,8 |
2,6 |
|
6 |
0,9 |
1 |
1 |
1,9 |
|
7 |
1 |
0 |
0 |
1 |
|
8 |
0 |
0 |
8 |
2,5 |
2,5 |
1 |
0,4 |
7 |
2,5 |
2,9 |
|
2 |
0,5 |
6 |
2,4 |
2,9 |
|
3 |
0,6 |
5 |
2,3 |
2,9 |
|
4 |
0,7 |
4 |
2,1 |
2,8 |
|
5 |
0,8 |
3 |
1,9 |
2,7 |
|
6 |
0,9 |
2 |
1,8 |
2,7 |
|
7 |
1 |
1 |
1 |
2 |
|
8 |
1,1 |
0 |
0 |
1,1 |
