Исследование_Операций_ЛР2

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н. Н. Григорьева
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №2

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. ТРАНСПОРТНЫЕ ЗАДАЧИ.

по курсу: ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы:

Научиться решать транспортные задачи без ограничений и с ограничениями, применяя различные методы решения.

Индивидуальное задание:

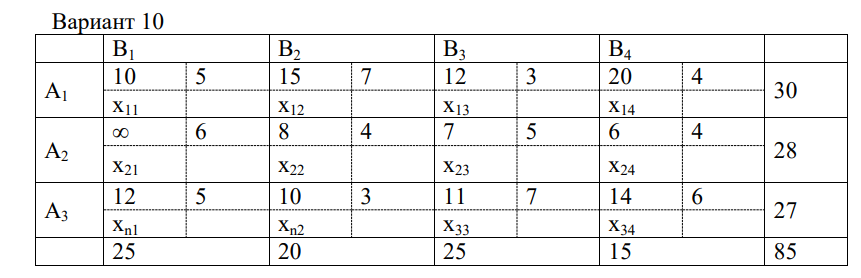
Теоретические сведения:

- Имеется n пунктов отправления некоей продукции A1, A2,… An и m пунктов получения этой продукции B1, B2,… Bm;

- В пункте отправления Ai содержится ai единиц продукции, а в пункте назначения Bj требуется bj единиц продукции;

- Между каждым пунктом отправления Ai и каждым пунктом назначения Bj существует коммуникация Ai→Bj ;

- Стоимость перевозки единицы продукции по маршруту Ai→Bj составляет Cij;

- Количество единиц продукции, отправляемой из пункта Ai в пункт Bj обозначаем xij

Ход работы:

В полученном варианте есть 3 пункта отправления и 4 пункта получения продукции. Необходимо составить такой план перевозок, чтобы вся продукция из пунктов отправления была полностью вывезена, все заявки пунктов назначения выполнены, а транспортные расходы на перевозки минимальны. В данном случае, количество продукции в пунктах назначения равняется числу продукции в пунктах отправления (85), значит это задача с правильным балансом и для неё можно сформулировать математическую постановку следующим образом:

Где целевая функция:

Исходная задача БЕЗ учета ограничений была перенесена в MS Excel, как показано на Рисунке 1.

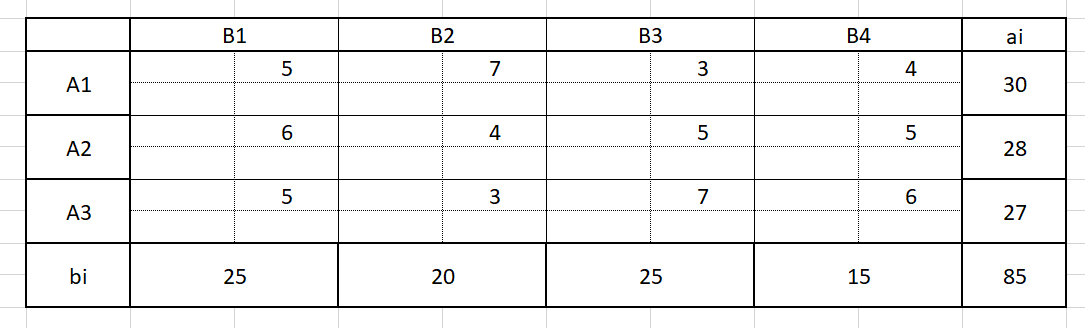
Рисунок 1 – Представление поставленной задачи в MS Excel

Далее задача была решена следующими способами:

1. Метод северо-западного угла

Работа алгоритма начинается с верхней левой клетки (северо-западной) (A1,B1). Выбрано наименьшее значение между b1 и a1. В данном случае это b1=25. Столько единиц груза выпишем через 1-ый склад. Таким образом, полностью удовлетворена заявка первого потребителя, а запас 1-ого склада необходимо скорректировать a1=30-25=5. Рассмотрение ячеек осуществляется далее со сдвигом справа и вниз, если на складе нет груза. В ячейке (A1;B2) заявка второго потребителя составляет b2=20. С 1-ого склада списано 5 оставшихся единиц. Следующие 15 единиц от заявки списаны со 2-ого склада (запас 13). Далее 3-яя заявка, со 2-ого склада списано 13 доступных единиц, оставшиеся 12 – с 3-его (запас 15). В 3-ей заявке необходимо 15 единиц, которые как раз остались на последнем складе.

Полученный таким образом план перевозок приведен в Таблице 1. Итоговая стоимость перевозок W равняется сумме произведений стоимости перевозки и количества груза в каждой ячейке, в данном случае 459.

Метод северо-западного угла
	B1		B2		B3			B4			ai
A1		5		7		3			4	30->5->0
	25		5		0		0
A2		6		4		5			5	28->13->0
	0		15		13		0
A3		5		3		7			6	27->15->0
	0		0		12		15
bj	25->0		20->15->0		25->12->0			15->0			459

Таблица 2 – Результат применения метода северо-западного угла

2. Метод Фогеля

На каждом шаге алгоритма для каждой строки и каждого столбца определяется разница между двумя минимальными стоимостями по этой строке / столбцу. На первом шаге для строк это будут значения (1, 1, 2); а для столбцов - (1, 1, 2, 1). Для заполнения выбирается строка или столбец с максимальной разницей, в данном случае это либо 3 столбец, либо 3 строка. Выбран столбец, так как в нем в ячейке (A1;B3) с такой же минимальной стоимостью (3) как и в ячейке 3 строки (A3,B2) больше груза – 25 > 20. Итак, в 3 столбце вывезен весь груз, а на складе осталось 5 единиц. Третий столбец можно вычеркнуть. Далее заново расставляются разности между стоимостями: (1,1,2) для строк и (1,1,-,1) для столбцов. Теперь выбирается минимальная стоимость в 3 строке: ячейка (A3;B2). Туда выписан весь груз 20, остаток на складе 7. Расстановка разниц: (1,1,1) для строк и (1,-,-,1) для столбцов. Нет максимальной разницы, поэтому выбирается доступная ячейка с минимальной стоимостью – (A1;B4). Туда можно выписать только 5 единиц груза из 15, ещё 10 выписываются со второго склада, так как стоимость перевозки там меньше, чем на третьем. Остался первый столбец, где 18 единиц груза уходят со второго склада, а оставшиеся 7 с третьего.

По Таблице 2 весь груз распределен, стоимость перевозок составила 348. Это значение значительно меньше, чем полученное методом С-З угла, что подтверждает большую эффективность использования метода Фогеля.

Метод Фогеля
	B1		B2			B3			B4			ai		D
A1		5			7			3			4		30->5->0		1,1,1
	0			0			25			5
A2		6			4			5			5		28->18		1,1,1
	18			0			0			10
A3		5			3			7			6		27->7		2,2,1
	7			20			0			0
bj	25		20->0			25->0			15->10->0			348
D	1,1,1		1,1			2			1,1,1

Таблица 1 – Результат применения метода Фогеля

Чтобы получить актуальное значение минимальной стоимости (348) методом С-З угла, проведена его оптимизация. Для этого использован метод “Поиск циклов с отрицательной ценой”. В Таблице 1 выделяется ячейка (A3;B4) с большой стоимостью перевозки и всем грузом заявки. Выполнено перераспределение, чтобы убрать данную перевозку:

Цена цикла:

за 15 единиц

Отрицательная цена цикла показывает, сколько будет сэкономлено на перевозке единицы груза по данному циклу. По данной перевозке можно перенести 15 единиц груза, соответственно общая стоимость уменьшится на (-2) * 15 = 30 и будет составлять 459-30 = 429. Результат улучшился, но он всё еще не оптимален. На данном шаге актуальные значения представлены в Таблице 3.

Оптимизация плана С-З угла. Переброска: 34—14—11—31
	B1		B2		B3		B4		ai
A1		5		7		3		4	30->10->0
	10		5		0		15
A2		6		4		5		5	28->13->0
	0		15		13		0
A3		5		3		7		6	27->12->0
	15		0		12		0
bj	25->15->0		20->15->0		25->12->0		15->0		429

Таблица 3 – Результат выполнения цикла с отрицательной ценой -2

Следующий цикл составлен от ячейки (A3;B3), где 12 единиц груза перевозятся при наибольшей стоимости 7. Пусть данный груз перевозится с 1-го склада, но там не хватает 2 единиц, которые переведены на 2-ой склад. Тогда заявку 1-го потребителя нужно вывозить с 3-го склада, а заявку второго потребителя частично вывести с 3-его склада. Тогда циклы переброски:

Цены циклов:

за 10 единиц

за 12 единиц

Результаты перебросок отображены в Таблице 4. Общая стоимость уменьшилась на 46 единиц и стала равняться 383, что еще не оптимально, поэтому оптимизация продолжена.

Оптимизация плана С-З угла. Переброски: 33—13—11—31 ; 33—23—22—32
	B1		B2		B3			B4			ai
A1		5		7			3			4		30->25->15->0
	0		5			10			15
A2		6		4			5			5		28->15->0
	0		13			15			0
A3		5		3			7			6		27->2->0
	25		2			0			0
bj	25->0		20->15->2->0		25->15->0			15->0			383

Таблица 4 – Результат выполнения циклов с отрицательными ценами -4 и -3

Теперь задача избавиться от перевозки (A2;B3), как самой дорогостоящей. Переписать весь груз 3-ей заявки груз можно записать на 1-ый склад, тогда там останется 5 единиц, которые вывозятся по 2-ой заявке. Еще 15 единиц требуются по 4-ой заявке, их можно переписать на 2-ой склад, где как раз осталось 15 единиц, после удаления перевозки (A2;B3). Таким образом осуществлен цикл:

Цена цикла:

за 15 единиц

Результаты перераспределения отображены в Таблице 5. Общая стоимость уменьшилась на 15 единиц и стала равной 368, что не оптимально, поэтому оптимизация продолжена.

Оптимизация плана С-З угла. Переброска :
	B1		B2		B3			B4			ai
A1		5		7		3			4	30->25-0
	0		5		25		0
A2		6		4		5			5	28->15->0
	0		13		0		15
A3		5		3		7			6	27->2->0
	25		2		0		0
bj	25->0		20->15->2->0		25->15->0			15->0			368

Таблица 5 – Результат выполнения цикла с отрицательной ценой -1

Следующая перевозка для замены – (A2;B4;), где стоимость перевозки составляет 75. Изменив склад с 2-го на 1-ый, тогда запишем часть груза 2-ой заявки на 2-ой склад, так как на 1-ом складе нет груза, для полного закрытия 4-ой заявки. Получен цикл:

Цена цикла:

за 5 единиц

Результаты перераспределения отображены в Таблице 6. Общая стоимость уменьшилась на 20 единиц и стала равной 348, что совпало с результатом, найденным методом Фогеля, поэтому оптимизация закончена.

Оптимизация плана С-З угла. Переброска: 24—12—12—22
	B1		B2		B3		B4		ai
A1		5		7		3		4	30->5->0
	0		0		25		5
A2		6		4		5		5	28->18->0
	0		18		0		10
A3		5		3		7		6	27->2->0
	25		2		0		0
bj	25->0		20->2->0		25->0		15->10->0		348