Исследование_Операций_ЛР1

ГУАП

КАФЕДРА № 41

ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

Старший преподаватель				Н. Н. Григорьева
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. ГРАФИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ И СИМПЛЕКС-МЕТОД.

по курсу: ИССЛЕДОВАНИЕ ОПЕРАЦИЙ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	4117
			подпись, дата		инициалы, фамилия

Санкт-Петербург 2024

Цель работы:

Изучение разных способов решения задачи линейного программирования. Освоение графического метода решения, симплекс-метода и составления двойственной задачи.

Индивидуальное задание: вариант № 10

Ход работы:

Необходимо найти неотрицательные значения x1 и x2, при которых целевая функция L будет иметь максимальное значение. Данную задачу линейного программирования можно решить несколькими способами:

1. Графический способ:

По заданным ограничениям строится область допустимых решений (ОДР) для x1 и x2, после чего в критических точках области сравниваются значения целевой функции и выбирается наибольшее.

Для построения ОДР данные неравенства были приведены к следующей системе:

В соответствии с Рисунком 1 построены по этим функциям построены графики и, учитывая знаки неравенств и не отрицательность переменных, была выделена треугольная область (зелёная штриховка) допустимых решений.

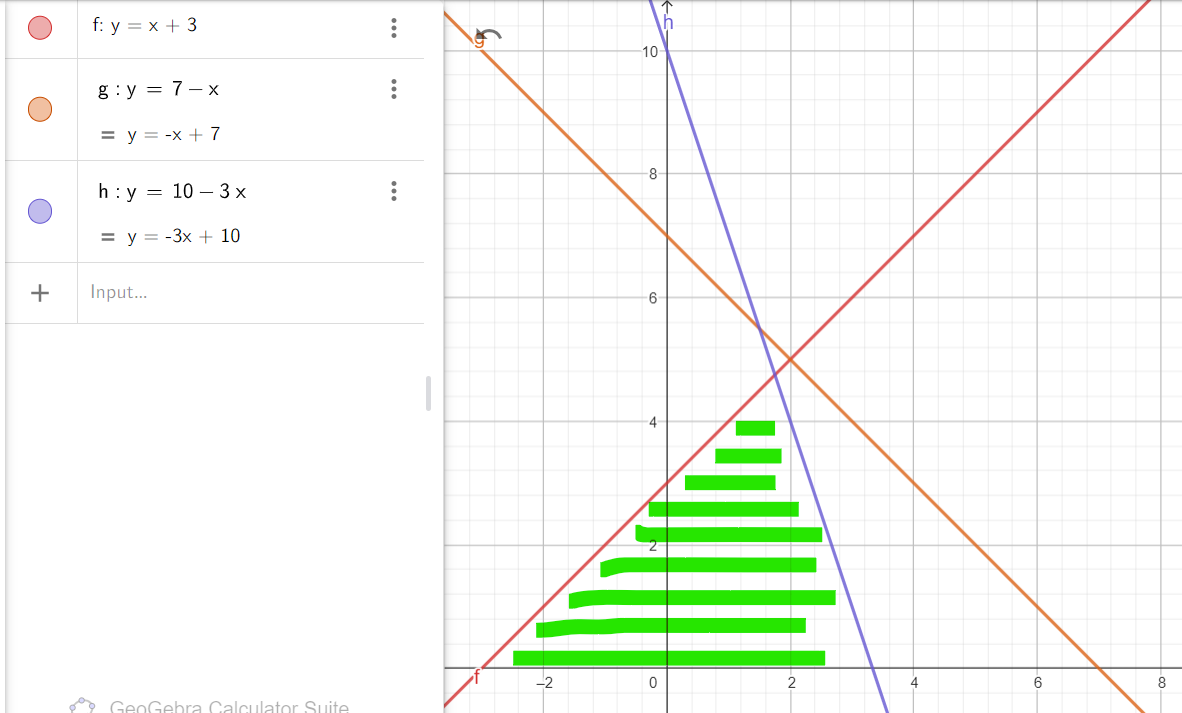
Рисунок 1 – Полученная область допустимых решений

Целевая функция L = x1+2x2 будет иметь максимум в наивысшей точке ОДР, так как коэффициент у x2 выше чем у x1. Для нахождения этой точки рассмотрено пересечение 1 и 3 функций:

Подставив найденные x1 и x2 получается следующее значение ЦФ:

2. Симплекс-метод:

Второй способ решения симплекс-метод - аналитический способ, основанный на добавлении дополнительных переменных. В начале исходная система приводится к каноническому виду: знаки во всех неравенствах одинаковые. В данном варианте уже канонический вид, тогда при выражении уравнений через новые переменные получилась система:

Знаки исходных уравнений изменены, а значит ЦФ будет стремится к минимуму:

Переменные y1,y2,y3 взяты как базисные, а x1,x2 – как свободные. В таком случае x1,x2 можно считать нулевыми, тогда предполагаемое решение:

Для оптимизации x2 взята как базисная переменная вместо y1, так как в ЦФ при x2 наибольший коэффициент, а в решении минимальное значение при y1. Тогда базисные : x2,y2,y3; Свободные: x1,y1; Выразив x2 через y1 получилась следующая система:

Решение некорректно, в ЦФ есть положительный элемент. Следующей в базисные переменные взята x1, так как при ней в ЦФ наибольший по модулю коэффициент. Если выразить через неё другие переменные то получается:

При подстановке y3;y1 = 0 наименьшее значение получается при замене y3: 7/4. Поэтому в следующей системе x1 будет заменена на y3.

Теперь ЦФ удовлетворяет условиям, значит максимальное значение

, что совпадает со значением найденным графическим методом.

3. Табличный симплекс-метод:

Решение задачи также может быть найдено с использованием MS Excel и симплекс-метода в поиске решений. На рисунках 2-3 показано внесение данных для поиска и результаты решения задачи. Полученный ответ подтвердил результаты графического и аналитического способов.

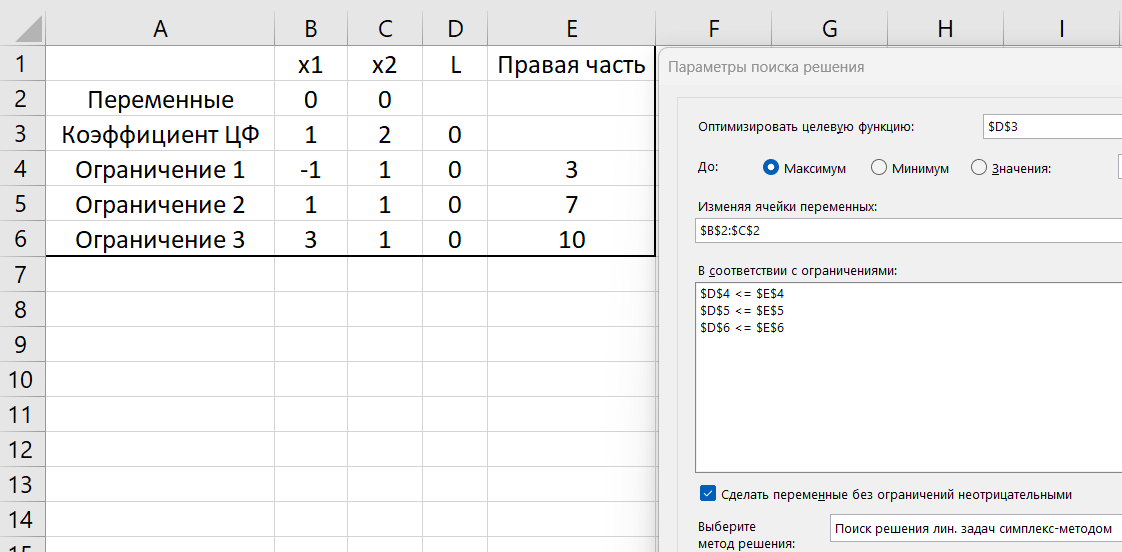
Рисунок 2 – Внесение данных в MS Excel

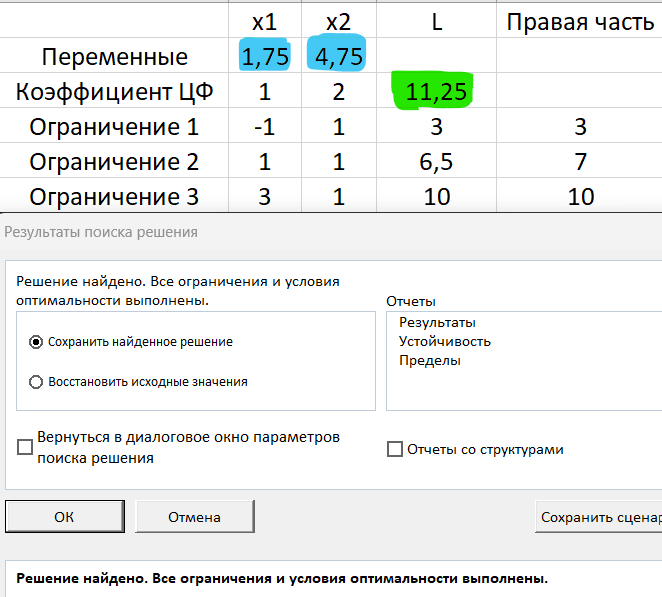
Рисунок 3 – Результата поиска решений в MS Excel

4. Составление и решение двойственной задачи:

Для составления двойственной задачи в исходная задача записана в стандартной форме, по ограничениям выделено 3 двойственных переменных y1,y2,y3.

Исходная задача:

Стандартная форма с двойственными переменными y:

В исходно задаче ЦФ стремится к максимуму, поэтому в двойственной она будет стремиться к минимуму, а знаки ограничений будут заменены на противоположные. Коэффициенты для ЦФ берутся из правой части ограничений исходной функции, а коэффициенты при двойственных переменных в новых ограничениях соответствуют коэффициентам при x1,x2,x3 в каждой строке. Правая часть ограничений берется из коэффициентов при ЦФ.

Двойственная задача:

Для решения построенной двойственной задачи можно также воспользоваться поиском решений в MS Excel, заполнив таблицу для решения симплекс-методом. Составленная таблица приведена на Рисунке 4.

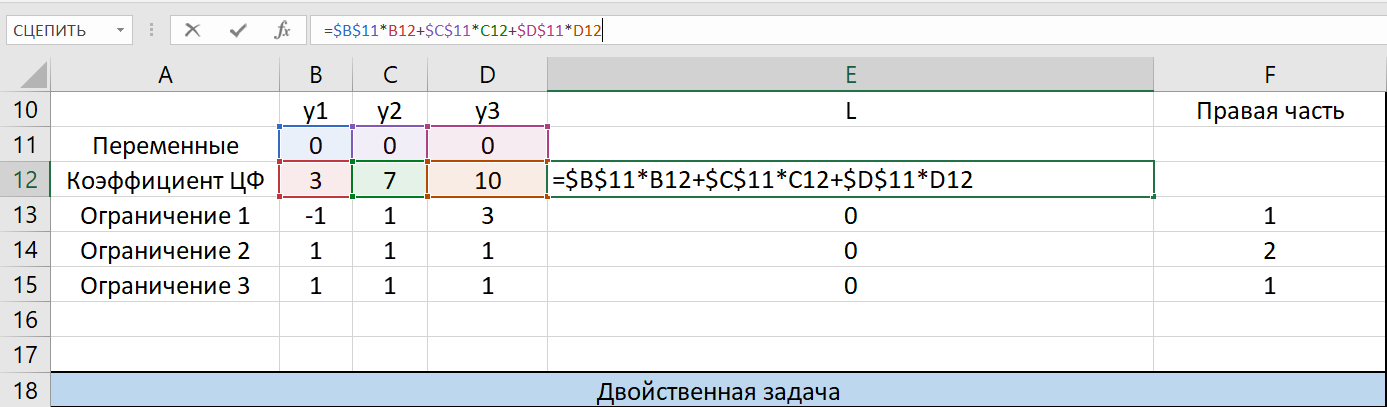
Рисунок 4 – Параметры двойственной задачи в MS Excel

Параметры для поиска решений показаны на Рисунке 5. В отличие от исходной задачи, в двойственной ЦФ стремится к минимуму, и изменены знаки ограничений. Результат применения поиска решений продемонстрирован на Рисунке 6. Решение совпало с ранее найденным.

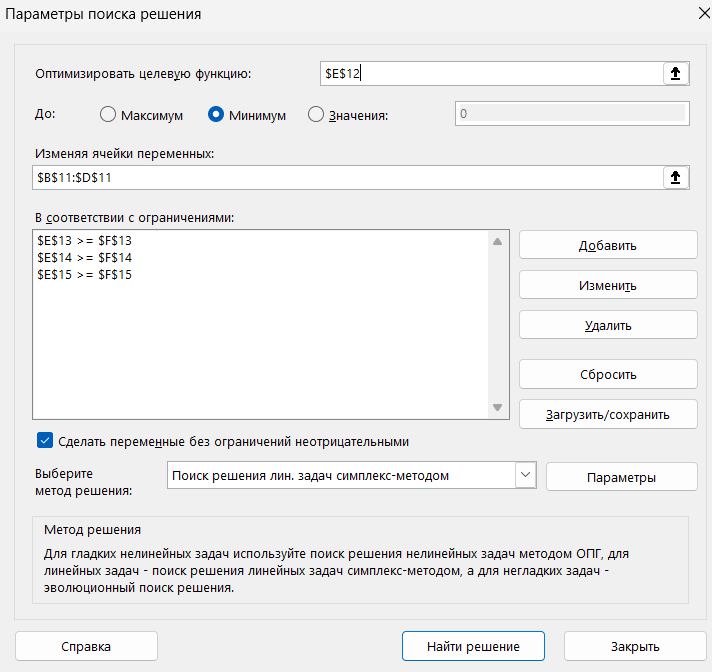
Рисунок 5 – Параметры поиска решений для двойственной задачи

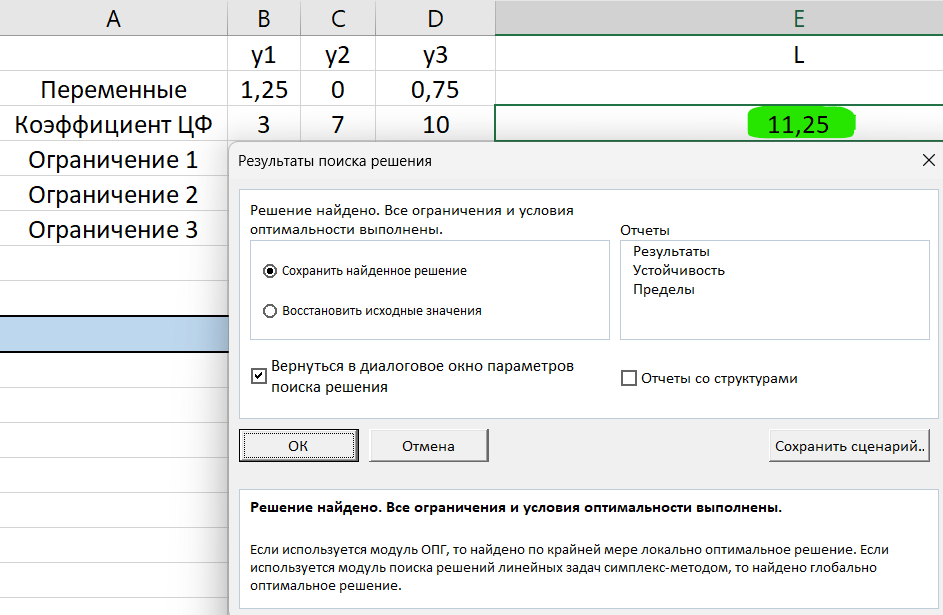
Рисунок 6 – Результат поиска решений

Вывод:

В ходе выполнения лабораторной работы были изучены разные способы решения задач линейного программирования. Освоен графический метод, реализация которого заключается в построении на плоскости ОДР и подборе наибольшего / наименьшего значения целевой функции в данной области.

Опробован аналитический способ решения симплекс-метод, строящийся на введении новых элементов и подборе базисных и свободных переменных в получении удовлетворительных коэффициентов.

Также получен опыт работы с инструментом поиск решений в MS Excel, в частности с симплекс-методом, для быстрого и более удобного способа решения линейной задачи программирования.

Изучено построение двойственной задачи. Её проще решать, когда в исходной задаче много переменных, но мало ограничений. Сформулированную двойственную задачу можно также как и прямую перенести в Excel и получить ответ, применив поиск решений симплекс-методов.