4 Ряды Фурье

300. Задание {{ 302 }} ТЗ № 302

Разложение функции в ряд Фурье по косинусам имеет вид:







 1+

301. Задание {{ 303 }} ТЗ № 303

Разложение функции y=x² в интервале (0, ) в ряд Фурье синусов имеет вид:









302. Задание {{ 304 }} ТЗ № 304

Разложение функции f(x)=x в ряд Фурье на интервале (- ) имеет вид:



 2

 3

 4

303. Задание {{ 305 }} ТЗ № 305

Разложение функции f(x)= (0<h< ) в неполный ряд Фурье по косинусам равна:









304. Задание {{ 306 }} ТЗ № 306

Разложение функции f(x)=xcosx в неполный ряд Фурье на интервале (0; по синусам равна:



 sinx+

 -

 1+

305. Задание {{ 307 }} ТЗ № 307

Разложение функции f(x)= в ряд Фурье в интервале (0;2 ) имеет вид:







 2

306. Задание {{ 308 }} ТЗ № 308

Разложение функции 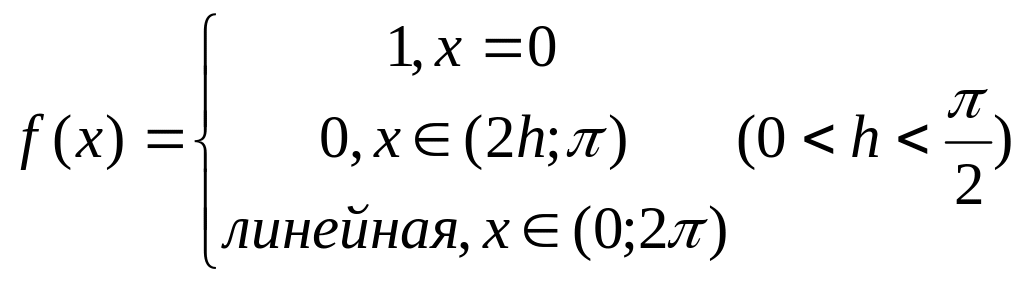в неполный ряд Фурье по косинусам имеет вид:









307. Задание {{ 309 }} ТЗ № 309

Разложение функции в неполный ряд Фурье по синусам имеет вид:









308. Задание {{ 310 }} ТЗ № 310

Разложение в ряд Фурье функции f(x)=e^-x в интервале (- ) имеет вид:









309. Задание {{ 311 }} ТЗ № 311

Разложение в неполный ряд Фурье функции по косинусам имеет вид:









310. Задание {{ 312 }} ТЗ № 312

Разложение в неполный ряд Фурье функции f(x)=x² в интервале (0; ) по синусам имеет вид:









311. Задание {{ 313 }} ТЗ № 313

Разложение периодической функции в ряд Фурье равна:









312. Задание {{ 314 }} ТЗ № 314

Разложение функции в неполный ряд Фурье на интервале по косинусам равна:









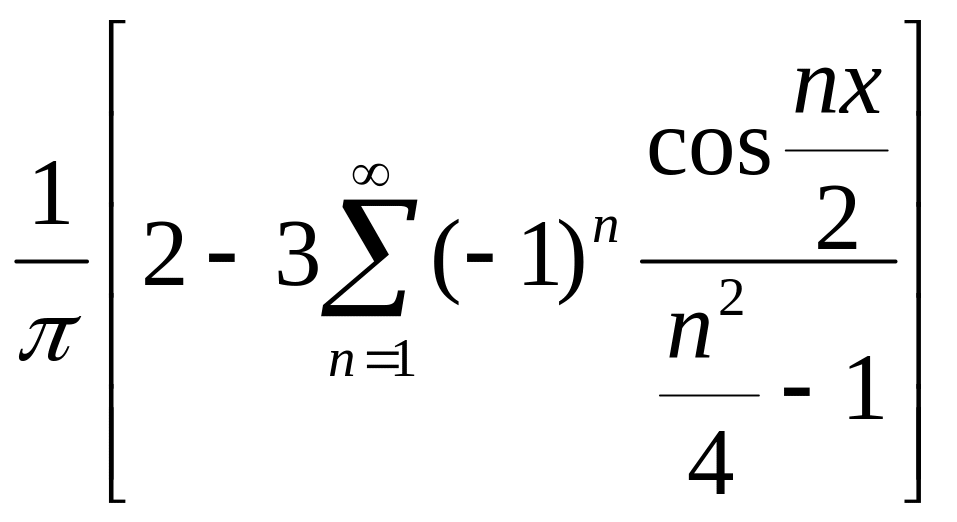
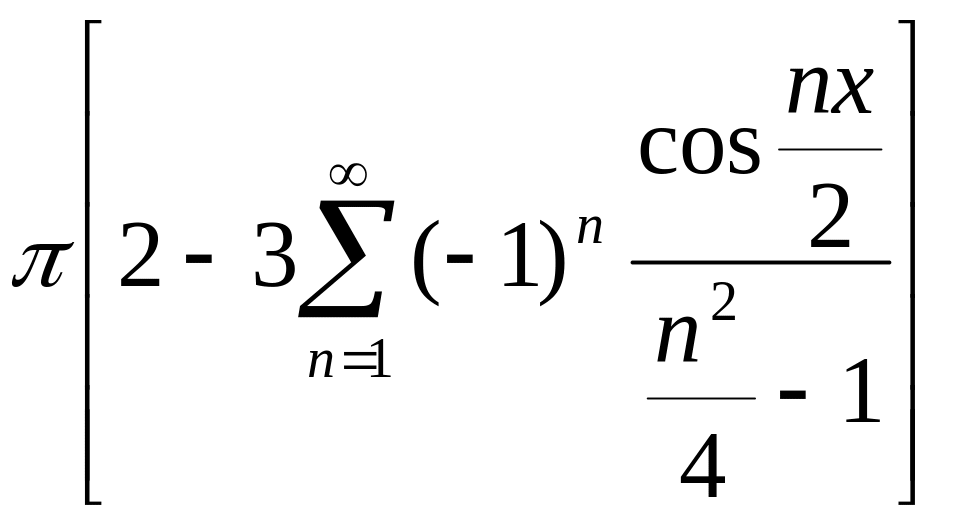
313. Задание {{ 315 }} ТЗ № 315

Разложение функции в интервале в неполный ряд Фурье по синусам равна:









314. Задание {{ 316 }} ТЗ № 316

Разложение функции равной –1 в интервале и 1 в интервале в ряд Фурье имеет вид:









315. Задание {{ 317 }} ТЗ № 317

Разложение функции в интервале в ряд Фурье по синусам имеет вид:









316. Задание {{ 318 }} ТЗ № 318

Разложение функции в интервале в ряд Фурье по косинусам имеет вид:









317. Задание {{ 319 }} ТЗ № 319

Разложение функции в интервале в ряд синусов имеет вид:









318. Задание {{ 320 }} ТЗ № 320

Разложение функции в интервале в неполный ряд Фурье, содержащий только синусы имеет вид:









319. Задание {{ 321 }} ТЗ № 321

Разложение функции в ряд Фурье при имеет вид:









320. Задание {{ 322 }} ТЗ № 322

Разложение функции при в ряд Фурье имеет вид:







 Разложение функции в ряд Фурье на имеет вид:









322. Задание {{ 324 }} ТЗ № 324

Разложение функции в ряд Фурье, при , с периодом , имеет вид









323. Задание {{ 325 }} ТЗ № 325

Разложение в ряд Фурье периодической, с периодом , функции , при , причем , имеет вид









324. Задание {{ 326 }} ТЗ № 326

Разложение функции в ряд Фурье имеет вид









325. Задание {{ 327 }} ТЗ № 327

Ряд Шмар периодической, с периодом , функции и , имеет вид









326. Задание {{ 328 }} ТЗ № 328

Неполный ряд Фурье, содержащий только косинусы, периодической, с периодом функции , имеет вид









327. Задание {{ 329 }} ТЗ № 329

Разложение в ряд Шмар по синусам функции в интервале , имеет вид









328. Задание {{ 330 }} ТЗ № 330

Разложение в неполный ряд Фурье, содержащий только косинусы, функции имеет вид









329. Задание {{ 331 }} ТЗ № 331

Неполный ряд Фурье, содержащий только синусы, функции на имеет вид









3 РЕЙТИНГОВАЯ ТОЧКА

1 Дифференциальные уравнения

2 Дифференциальные уравнения в частных производных

3 Операционное исчисление