
Какие-то билеты / Билет 15
.pdf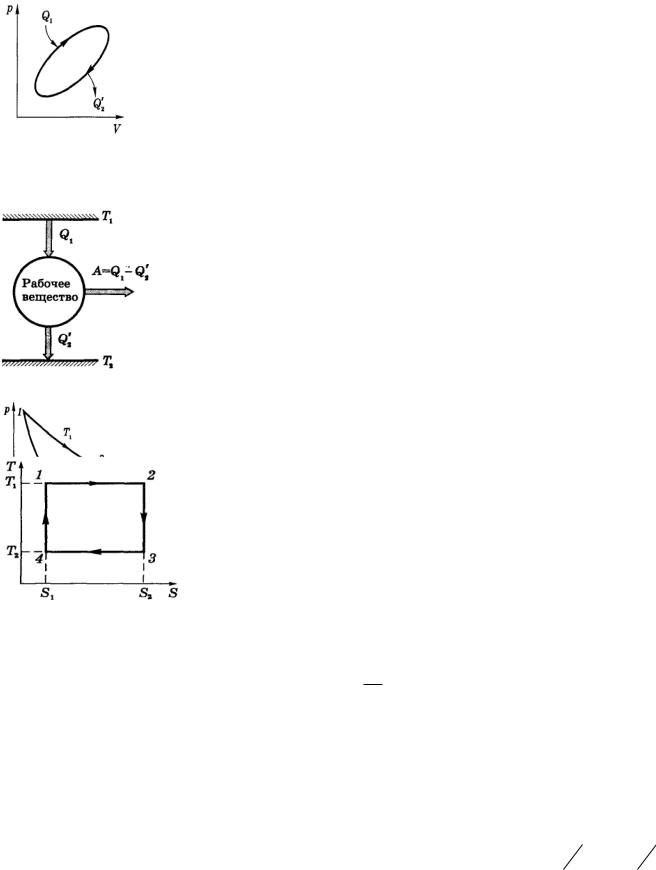
1. КПД тепловой машины. КПД цикла Карно.
Периодически действующий двигатель, совершающий работу за счет получаемой извне теплоты, называется тепловой машиной. Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс. Совершая цикл, рабочее вещество возвращается в исходное состояние. По этому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемое рабочему телу за цикл, равно Q1—Q’2 где Q1 – теплота, получаемая рабочим телом. Q2 - теплота отдаваемая. Таким образом, ворожение для цикла имеет вид: А= Q1—Q’2. Если процесс совершается по часовой стрелке, то работа, производимая двигателем за цикл, А > 0.
Тепловую машину принято характеризовать коэффициентом полезного действия: |
A |
1 |
Q |
|
|
; |
2 |
||
Q |
Q1 |
|||
Рассмотренный Карно тепловой двигатель состоял из нагревателя с температурой ТI, холодильника с Т2 и рабочего тела, т.е. устройства, способного получать тепло и совершать работу. Под рабочим телом пока будем понимать идеальный газ в цилиндре с поршнем. Карно рассмотрел цикл из двух изотерм и двух адиабат . При изотермическом расширении 1-2 газ находится в контакте с нагревателем (T1). Пусть при этом газ получает тепло Q1. На изотерме 3-4 газ отдает тепло Q2 холодильнику (T2).
|
1 |
Q |
|
2 |
|
КПД двигателя: |
Q |
|
|
|
1 |
Данный цикл является обратимым (если его проводить бесконечно медленно). Он может быть проведен в обратном направлении, и при этом газ совершает отрицательную работу, нагреватель получает обратно тепло Q1;
холодильник отдает газу тепло Q2, которое он получил в прямом цикле. Именно так в принципе работает любой бытовой холодильник. Дальнейшие рассуждения проще всего провести, изобразив цикл Карно не на диаграмме р, V, а на диаграмме S, Т (энтропия — температура). На этой диаграмме цикл Карно имеет вид прямоугольника (рис. 3.6). Изотермы изображаются прямыми 1-2 и 3-4, адиабаты — прямыми 2- 3 и 4-1. Согласно (3.3) полученное тепло Qi = T'i(S2 - Si) и равно площади под отрезком 1-2. Отданное холодильнику тепло Q2 = T2(SZ - Si) и равно площади под отрезком 4-3. При этом площадь прямоугольника, т.е. Qi - Q2, равна работе А, совершаемой
двигателем за цикл. Подставив выражения QJ и Q2 в формулу (3.1), получим, что КПД цикла Карно:
1 T2
T1
При выводе этой формулы не делалось никаких предположений о свойствах рабочего вещества и устройстве теплового двигателя. Отсюда следует знаменитая теорема Карно:КПД обратимых двигателей, работающих по циклу Карно, зависит только от температур Tt и Т2 — нагревателя и холодильника, но не зависит ни от устройства двигателя, ни от рода рабочего вещества.
2. Затухающие колебания
|
|
2 |
2 |
r |
m |
2 |
|
k |
m (r – |
Затухающие колебания описываются уравнением x |
2 x 0 x 0 , где |
|
0 |
|
|||||
коэффициент сопротивления т.е. коэффициент пропорциональности между скоростью x’ и силой сопротивления; k – коэффициент квазиупругой силы).
0 представляет собой ту частоту, с которой совершались колебания системы в отсутствии сопротивления среды (r=0). Эту частоту называют собственной частотой системы.
Решение уравнения затухающих колебаний.
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 x |
0 x 0 |
|
|
|
|
|
|
|
|
|
2 e t 2 e t 02 e t |
0 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
e |
t |
|
e |
t |
|
|
|
2 |
e |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 2 2 |
0 2 2 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||
x(t) e |
|
2 |
02 t |
c2 e |
2 02 |
|
|
|
|
|
|
|
||||||||||||||||
|
c1e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) При >0 |
возникает апериодическое движение. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|||
|
|
|
|
|
x(t) e |
|
|
|
|
i |
02 2 t |
c2 e |
i |
02 2 |
|
|
||||||||||||
2) При <0 |
|
|
c1e |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x(t) e t a |
0 |
cos( |
|
2 2 t ) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
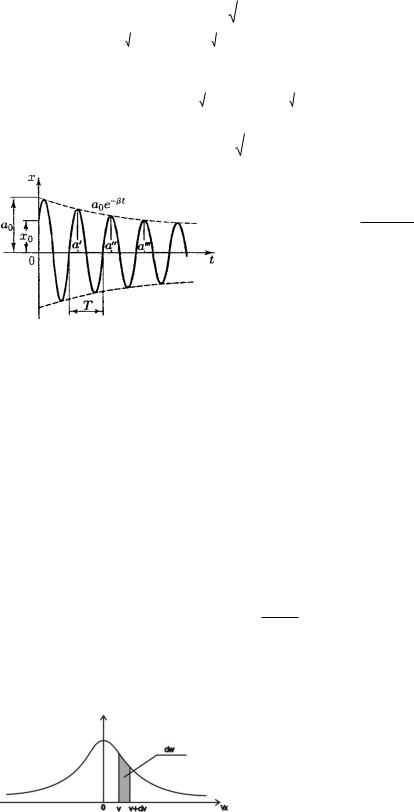
Такие колебания не являются гармоническими так как амплитуда зависит от значения t. Таким образом общее решение для уравнения затухающего колебания выглядит так:
x(t) e t a0 cos(
 20 2 t )
20 2 t )
Здесь а0 и - произвольные постоянные. На графике штриховыми линиями показаны пределы, в которых находится смещение колеблющейся точки х.
3. Функции распределения вероятностей для составляющих скорости молекул ид. Газа
Т. к. dwv=f(v)dv=φ(vx)dvxφ(vy)dvyφ(vz)dvz → dP(vx ) |
dN (vx ) |
(vx )dvx , |
|
N |
|||
|
|
где φ(vx) – функция распределения по vx. Вероятности того, что молекула имеет проекции скорости в интервалах (vx, vx+dvx), (vy, vy+dvy), (vz, vz+dvz), являются независимыми, поэтому в соответствии с теоремой об умножении вероятностей независимых событий можно записать:
dP(vx , vy , vz ) dP(vx )dP(vy )dP(vz )
(vx ) (vy ) (vz )dvx dvy dvz
Отсюда получаем, что f(v)=φ(vx)φ(vy)φ(vz).
|
1 |
||
|
m |
|
|
2 |
|||
Откуда (vx ) |
|
|
|
|
|||
|
2 kT |
||
(vx )dvx 1
exp
mv2
x
2kT . Функция нормирована на единицу. Т.е.
График зависимости φ(vx) от vx
