Какие-то билеты / Билет 11

1.Вынужденные колебания. Резонанс

Вслучае, когда вынуждающая сила изменяется по гармоническому закону, колебания описываются дифференциальным уравнением следующего вида:

Здесь - коэффициент затухания, 0 – собственная частота системы, f0=F0/m (F0 - амплитуда вынуждающей силы), - частота вынуждающей силы.

Т.к. уравнение вынужденных колебаний является неоднородным, то его решение состоит из суммы общего и частного решения. Общее решение нам известно:

Частное решение можно получить с помощью векторной диаграммы. Предположим частное решение

имеет вид x=acos( t- ), тогда:

x a sin( t ) a cos( t 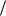2)x 2a cos( t ) 2a cos( t )

Подставляя полученное в исходное уравнение (1) получаем:

2 a cos( t ) 2 a cos( t 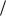2) 02 a cos( t )

f 0 cos( t)

Ввиде векторных диаграмм это будет выглядеть так ( случай а) - < 0; случай б) - > 0):

f 02 a 2 ( 02 2 ) 4 a 2 2

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для системы частоте амплитуда колебаний достигает максимального значения. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

РЕЗ 20 2 2

Изображенная на рисунке совокупность графиков функций, соответствующих различным значениям параметра , называется резонансными кривыми.

По поводу резонансных кривых можно сделать еще следующие замечания: при стремлении к нулю все кривые приходят к одному и тому же, отличному от нуля предельному значению, равному F0 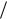(m 20 ) т.е. F0/k.

Зависимость от при разных значениях показан графически на графике (слева). Частоте 0 соответствует = /2. Резонансная частота меньше собственной. Следовательно в момент резонанса

< /2. При слабом затухании рез 0, и значение при резонансе можно считать равным /2.

2. Работа Газа при адиабатическом процессе

Если известна для некоторого обратимого процесса зависимость давления газа от объема, т.е.

функция p=f(V) работа, совершаемая в ходе этого процесса, вычисляется путем интегрирования:

V2

(начальном) и втором (конечном) состояниях, р и V — давление и объем в любом промежуточном

состоянии. Выразим в соответствии с этим соотношением давление газа через его объем и значения параметров в начальном состоянии: p=p1V1n/Vn

выражение можно преобразовать, воспользовавшись тем, что, какой бы процесс ни происходил с идеальным газом, его параметры связаны уравнением состояния. В частности, это справедливо и для

3. Агрегатное состояние вещества. Теплоѐмкость кристаллов. Закон Дюлонга-Пти.

Теплоемкость кристалла. Зная У(Г), находим, что теплоемкость единицы объема кристалла

Введем так называемую характеристическую температуру Дебая θ, определяемую условием

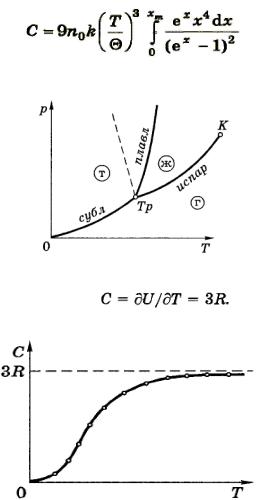
а также пешую переменную х — hv /kT. Тогда выражение для теплоемкости примет вид

где хт = hv /kT = θ/T. Выражение называют формулой Дебая

Отметим еще, что дебаевская температура θ указывает для каждого твердого тела область температур (T<θ), где становится

существенным квантование энергии колебаний.

В основе классической теории теплоѐмкости твѐрдых тел лежит закон равно распределения энергии по степеням свободы. Твѐрдое тело рассматривается как систему N независимых друг от друга атомов, имеющих по три колебательных степени свободы. На каждую из них приходиться в среднем энергии kT (kT/2

кинетической и kT/2 потенциальной). Имея в виду, что число колебательных степеней свободы 3N, получим, что внутренняя

энергия одного моля атомов U= 3NАkT = 3RT отсюда молярная теплоѐмкость:

В этом суть закона Дюлонга-Пти, который утверждает, что молярная теплоѐмкость всех химически простых твѐрдых тел одинакова и равна 3R. Этот закон выполняется достаточно хорошо только при сравнительно высоких температурах. Опыт показывает что при низких температурах теплоѐмкость убывает, стремясь к нулю при Т -> 0, по закону C~T^3.