Какие-то билеты / Билет 8

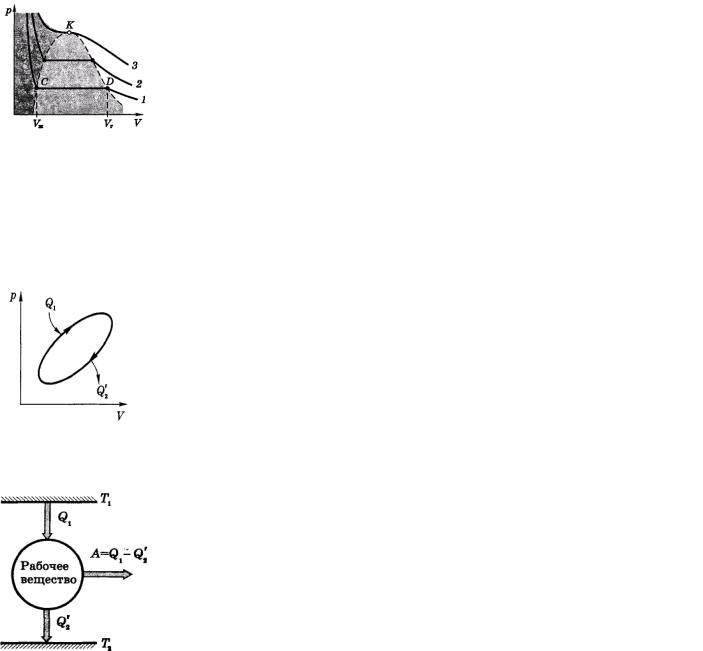
1.Пересыщенный пар и перегретая жидкость.

Экспериментальные изотермыто что дает эксперимент. Его результаты представлены на рис. Горизонтальный участок говорит о том, что с изотермическим увеличением объема газа его давление не меняется. Но горизонтальный участок наблюдается, и с ним связано новое явление. Прозрачный цилиндр с поршнем и внутри цилиндра — газ. Начнем его сжимать по изотерме 1 и следить за тем, что происходит в цилиндре. При достижении объема VГ цилиндр заполнен одним газом, но при дальнейшем сжатии наряду с газом появится жидкость, количество которой постепенно будет расти, а давление оставаться постоянным. Когда объем достиг нет Vж, он целиком окажется заполненным жидкостью.

Участок CD называется фазовый переход вещества из газообразного состояния в жидкое. Если фазовый переход происходит изотермически, то он совершается при р = const. Это общее свойство всех фазовых переходов: не только газообразной фазы в жидкую (и наоборот), но и жидкой фазы в твердую и т.д.

Фазой называют физически однородную часть вещества, отделенную от других частей системы границей раздела.

Всем горизонтальным изотермам в области под пунктирной кривой (она слабо тонирована) соответствуют двухфазные состояния — жидкость с паром, находящиеся в равновесии друг с другом. Такой пар называют насыщенным.

Левее двухфазной области расположена область, соответствующая одной фазе — жидкости (она тонирована сильнее). Здесь изотермы идут очень круто, что отвечает малой сжимаемости жидкости. Правее двухфазной области вещество находится в газообразном состоянии. Причем все состояния вне этой двухфазной области неплохо описываются уравнением Ван-дер-Ваальса. Это говорит о том, что данное уравнение описывает состояние вещества не только в газообразном, но и в жидком состоянии. Если газ начинают сжимать, например, по изотерме 1 (см, рис.), то он переходит в

двухфазное состояние (горизонтальный участок изотермы CD) жидкость + насыщенный пар. Объем жидкой фазы растет по мере приближения к точке С, после которой остается одна фаза — жидкость.

2.

КПД, Цикл Карно. КПД цикла Карно. Теорема Карно

Периодически действующий двигатель, совершающий работу за счет получаемой извне теплоты, называется тепловой машиной. Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс. Совершая цикл, рабочее вещество возвращается в исходное состояние. По этому изменение внутренней энергии за цикл равно нулю. Количество теплоты, сообщаемое рабочему телу за цикл, равно Q1—Q’2 где Q1 – теплота, получаемая рабочим телом. Q2 - теплота отдаваемая. Таким образом, ворожение для цикла имеет вид: А= Q1—Q’2. Если процесс совершается по часовой стрелке, то работа, производимая двигателем за цикл, А > 0.

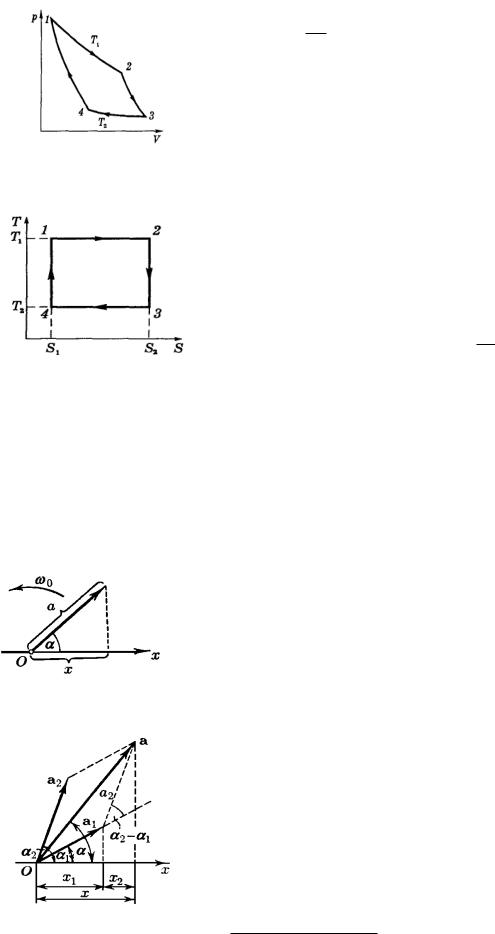
Рассмотренный Карно тепловой двигатель состоял из нагревателя с температурой ТI, холодильника с Т2 и рабочего тела, т.е. устройства, способного получать тепло и совершать работу. Под рабочим телом пока будем понимать идеальный газ в цилиндре с поршнем. Карно рассмотрел цикл из двух изотерм и двух адиабат . При изотермическом расширении 1-2 газ находится в контакте с нагревателем (T1). Пусть при этом газ получает тепло Q1. На изотерме 3-4 газ отдает тепло Q2 холодильнику (T2). КПД

Q

1 2 двигателя: Q1

Данный цикл является обратимым (если его проводить бесконечно медленно). Он может быть проведен в обратном направлении, и при этом газ совершает отрицательную работу, нагреватель получает обратно тепло Q1; холодильник отдает газу тепло Q2, которое он получил в прямом цикле. Именно так в принципе работает любой бытовой холодильник.

Дальнейшие рассуждения проще всего провести, изобразив цикл Карно не на диаграмме р, V, а на диаграмме S, Т (энтропия — температура). На этой диаграмме цикл Карно имеет вид пря-

моугольника (рис. 3.6). Изотермы изображаются прямыми 1-2 и 3-4, адиабаты — прямыми 2-3 и 4-1. Согласно (3.3) полученное тепло Qi = T'i(S2 - Si) и равно площади под отрезком 1-2.

Отданное холодильнику тепло Q2 = T2(SZ - Si) и равно площади под отрезком 4-3. При этом площадь прямоугольника, т.е. Qi - Q2, равна работе А, совершаемой двигателем за цикл. Подставив выражения QJ и Q2 в формулу (3.1), получим, что КПД цикла Карно:

1 T2

T1

При выводе этой формулы не делалось никаких предположений о свойствах рабочего вещества и устройстве теплового двигателя. Отсюда следует знаменитая теорема Карно:КПД обратимых двигателей, работающих по циклу Карно, зависит только от температур Tt и Т2 — нагревателя и холодильника, но не зависит ни от устройства двигателя, ни от рода рабочего вещества.

3. Сложение колебаний одного направления.

Решение ряда вопросов, в частности сложение нескольких колебаний одного направления (или, что то же самое сложение нескольких гармонических функций), значительно облегчается и становится наглядным, если изображать колебания графически в виде векторов на плоскости.

Полученная таким образом схема называется векторной диаграммой. Если привести вектор с длинной a во вращение с угловой скоростью 0, то проекция конца вектора будет перемещаться по оси х в пределах от –а до +а, причем координата этой проекции будет изменяться со временем по закону x=acos( 0t+ ). Следовательно гармоническое колебание может быть задано с помощью вектора, длина которого рав на амплитуде колебания, а направление

вектора образует с осью х угол, равный начальной фазе колебания.

При решении задачи на сложение двух колебаний одного направления возникают две различные задачи:

1)сложение колебаний с разными частотами т.е. 1 2, тогда получаем: x(t)=a1cos( 1t+ 1)+a2cos( 2+ 2) acos( t+ )

2)сложение колебаний с одинаковыми частотами т.е. 1= = 2, тогда

x(t)= a1cos( t+ 1)+a2cos( + 2)=acos( t+ ). Эту задачу проще всего решать с использованием векторной диаграммы.

Из построения видно, что

a2 a12 a22 2a1a2 cos( ( 2 1 ))a12 a22 2a1a2 cos( 2 1 )

tg a1 sin 1 a2 sin 2 a1 cos 1 a2 cos 2