Какие-то билеты / Билет 7
.pdf
1. Уравнение адиабаты идеального газа.
Процесс, протекающий без теплообмена с внешней средой, называется адиабатическим. Чтобы найти уравнение адиабаты идеального газа, т. е. уравнение, связывающее параметры состояния идеального газа при адиабатическом процессе, воспользуемся уравнением (1.11) первого начала
|
|
m |
|
|
|
|
|
m |
|
|
|
|
термодинамики, подставив в него выражение |
U |
|
CV T |
для U: |
d Q |
d |
|
CV T |
pdV |
(1.39) |
В |
|
M |
|
|||||||||||
|
|
|
|
|
M |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
отсутствие теплообмена с внешней средой |
d Q = 0. Поэтому для адиабатического процесса |
|||||||||||
|
|
|
|
pdV |
m |
C dT |
(1.40) |
|
|
|
||
уравнение (1.39) упрощается следующим |
образом: |
|
(мы |
произвели |
||||||||
|
M |
V |
|
|
|
|||||||
очевидные преобразования). Взяв дифференциал от обеих частей уравнения pV=(m/M)RT, придем к равенству pdV Vdp
Умножим уравнение (1.40) на отношение R/CV и сложим его с уравнением (1.41). В результате получим pdV+Vdp=0 (1.42), где =1+R/CV=CP/CV. Наконец, разделим (1.42) на произведение pV:dVV dpp 0 (1.43) Левую часть этого уравнения можно представить в виде d ln(pV ). откуда
следует, что pV =const. Мы получили уравнение адиабаты идеального газа в переменных р и V. Его
называют уравнением Пуассона. Представив уравнение (1.44) в виде pV V -1=const |
|
и учтя, что |
||||||||||
произведение рV пропорционально T, придем к уравнению адиабаты идеального газа в переменных |
||||||||||||
T и V: |
TV -1=const |
(1.45) |
(константы в формулах (1.44) |
и (1.45) |
имеют, |
разумеется, |
||||||
неодинаковое значение). |
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Затухающие колебания |
|
|
|
|
|
|
|
|
|
|
|
Затухающие колебания |
описываются |
|
|
2 |
где 2 |
r |
m |
2 |
|
k |
m (r – |
|
уравнением x |
2 x 0 x 0 , |
|
0 |
|
||||||||
коэффициент сопротивления т.е. коэффициент пропорциональности между скоростью x’ и силой сопротивления; k – коэффициент квазиупругой силы).
0 |
представляет собой ту частоту, с которой совершались колебания системы в отсутствии |
||||||||||||||||||||||||
сопротивления среды (r=0). Эту частоту называют собственной частотой системы. |
|||||||||||||||||||||||||
Решение уравнения затухающих колебаний. |
|
||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 x |
0 x 0 |
|
|
|
|
|
|
|
|
2 e t 2 e t 02 e t |
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
e |
t |
|
e |
t |
|
|
|
2 |
e |
t |
|
|
|
|
|
|
|
|
|
|
||||
x |
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 2 2 |
0 2 2 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|||
x(t) e |
|
2 |
02 t |
c2 e |
2 02 |
|
|
|
|
|
|||||||||||||||
|
c1e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) При >0 |
возникает апериодическое движение. |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|||
|
|
|
|
|
x(t) e |
|
|
|
i |
02 2 t |
c2 e |
i |
02 2 |
|
|||||||||||
2) При <0 |
|
|
c1e |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x(t) e t a0 cos(
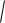20 2 t )
1.Такие колебания не являются гармоническими так как
амплитуда зависит от значения t. Таким образом общее решение для уравнения затухающего колебания выглядит так: x(t) e t a0 cos(
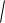20 2 t )
2. Здесь а0 и - произвольные постоянные. На графике штриховыми линиями показаны пределы, в которых находится смещение колеблющейся точки х.
3. Распределения Больцмана
4.