
Какие-то билеты / Билет 5
.pdf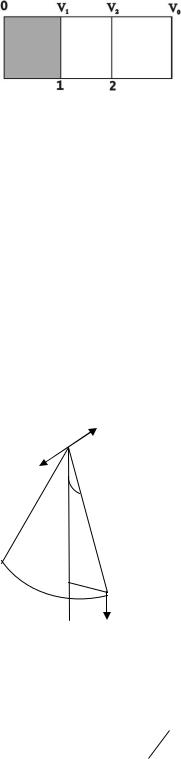
1. Энтропия и ее свойства |
|
|
В термодинамике энтропия определена как элементарное приращение dS |
Q |
. При этом |
|
T |
|
энтропия является именно функцией состояния.
Рассмотрим необратимый процесс расширения ид. газа в пустоту. V1 – первоначальный объем, V0 – полный объем. В данном случае газ не совершает работу, переданное газу тепло равно нулю, следовательно, по первому началу т/д приращение внутренней энергии тоже равно нулю, т.е. температура конечного и начального состояний одинакова. Т.к. энтропия – функция состояния, то вычислим ее работу по изотермическому процессу (т.к. он обратим). В изотермическом процессе
Q=A=νRTln(V2/V1) и S=Q/T=νRln(V2/V1)=kNln(V2/V1), N – число молекул в газе.
Обозначим за P1 = (V1/V0)N вероятность попадания N молекул в объем
V1, а за P2 = (V2/V0)N вероятность их попадания в V2. Тогда P2/P1 = (V2/V1)N и можно записать
ΔS=kNln(V2/V1)=kln(V2/V1)N =kln(P2/P1). А так как P~Ω, то получаем
ΔS=kln(Ω2/Ω1) и приходим к формуле Больцмана
S = k lnΩ
Энтропией (статистическое определение) называется величина S = k*lnΩ. Энтропия – мера беспорядка, т.е состояниям с большим беспорядком соответствует большая вероятность. Величина возрастания энтропии в замкнутой макросистеме может служить мерой необратимости процессов,
протекающих в системе. В предельном случае, когда процессы обратимы, то энтропия не изменяется. |
|||||
Свойства энтропии |
|
||||
1. Энтропия – аддитивная функция состояния, т.е. S = S1 + S2, энтропия полного цикла равна нулю. |
|||||
2. Энтропия замкнутой системы не убывает: S 0 |
|
||||
3. Теорема Нернста lim S 0 |
|
||||
|
|
|
|
T 0 |
|
2. Математический и физический маятники |
|
||||
В физике под маятником понимают твердое тело, совершающее под действием силы тяжести |
|
||||
колебания вокруг неподвижной точки или оси. Принято различать математический и физический |
|
||||
маятники. |
|
|
|
||
Математическим маятником называют идеализированную систему, состоящую из невесомой и |
|
||||
нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. |
|
||||
|
|
|
|
Достаточно хорошим приближением к математическому маятнику служит |
|
|
|
|
|
|
|
|
|
|
N |
небольшой тяжелый шарик, подвешенный на длинной тонкой нити. |
|
O |
|
|
Отклонение маятника от положения равновесия будем характеризовать углом |
, |
|
|
|
|
|||
|
|
||||
|
|
образованным нитью с вертикалью (см. рис.). При отклонении маятника от |
|
||
|
положения равновесия возникает вращательный момент N, равный mglsin (m – |
||||
|
|
|
|
||
масса, а l – длинна маятника). Он имеет такое направление, что стремится вернуть
маятник в положение равновесия, и аналогичен в этом отношении квазиупругой
l силе. Поэтому так же, как смещению и квазиупругой силе, моменту N и угловому смещению нужно приписывать противоположные знаки (рассматривая как вектор, связанный с направлением поворота правилом правого винта при <<1, противоположность знаков при N и можно объяснить тем, что векторы N и
mg направлены в противоположные стороны). Следовательно, выражение для вращательного момента имеет вид: N=-mglsin .
Напишем уравнение динамики вращательного движения для маятника, учитывая, что момент инерции маятника равен ml2, а угловое ускорение равно ”, получаем
ml2 mglsin gl sin 0 . Рассматривая малые колебания можем записать: sin .
Введем обозначение gl 20 .
Тогда мы придем к уравнению: 20 0 . Очевидно его решение имеет вид: =acos( 0t+ ).

Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим.
При отклонении маятника от положения равновесия на угол возникает вращающий момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен: : N=-mglsin , где m – масса маятника, а l – расстояние между точкой подвеса О и центром масс С маятника (см. рис.). Знак “минус” имеет то же значение, что и в случае математического маятника.
Обозначив момент инерции маятника относительно оси, проходящей через точку подвеса, буквой I, можно написать:
I mglsin
. В случае малых колебаний можем переписать уравнение:
20 0 . В данном случае через 20 обозначена следующая величина: 20 mglI
Примечание.
Если сравнить значения периодов колебания математического и физического маятника, то можно заметить, что математический маятник длинной lпр=I/(ml) будет иметь такой период колебаний, как и данный физический маятник. Данную величину называют приведенной длинной физического
маятника.
Точка, лежащая на расстоянии приведенной длинны от оси вращения на прямой, соединяющей точку подвеса с центром масс, называется центром качания физического маятника (см. точку O’).
3. Экспериментальное определение скоростей молекул газа
Наиболее вероятной скорости соответствует максимум функции распределения F(v). Эта скорость определяется из условия dF/dv=0, откуда следует
vвер 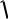
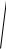 2 kTm
2 kTm 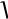
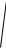 2 RTM
2 RTM
Средняя скорость по определению
Среднеквадратичная скорость vкв
|
kT |
|
|
v2 v2 F (v)dv 3 |
, т. е. |
||
m |
|||
0 |
|
||
|
|
Этот результат можно получить и
|
mv2 |
m v2 |
|
3 |
|
||
|
|
|
|
|
|
kT |
|
2 |
2 |
2 |
|||||
|
|
|
|
||||
F(U )
|
|
|
|
|
|
|
|
|
|
|
|
|
8 kT |
|
|
|
8 RT |
|
|||||
v vF(v)dv |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
m |
M |
|
|||||||||
0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|

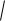 v2 находится из условия vкв
v2 находится из условия vкв 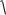
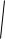 3 kTm
3 kTm 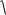
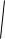 3 RTM
3 RTM
без интегрирования, а как следствие формулы 32 kT , т.е.
U U |
ñð.êâ. |
U |
âåð |
||
Ucð |
|
|
