Какие-то билеты / Билет 3

1. Свободные колебания системы без трения.

Колебаниями называют такие физические процессы, которые с той или иной степенью частотой повторяются во времени.

Колебания называются периодическими, если значения физических величин повторяются через равные промежутки времени: x(t)=x(t+T). Величина Т называется периодом колебаний.

Частотой колебаний называется число полных колебаний в единицу времени: =1/T.

Круговой (циклической) частотой называется величина =2 .

Свободными, или собственными, называются такие колебания, которые происходят в системе, предоставленной самой себе после того, как она была выведена из положения равновесия.

2. Основные законы термодинамики

1-ое начало:

Словами первое начало термодинамики формулируется следующим образом: количество

теплоты, сообщенное системе, идет на приращение внутренней энергии системы и на совершение системой работы над внешними телами. Подчеркнем, что речь идет о разности конечного и начального значений внутренней энергии.

При вычислении совершенной системой работы или полученной системой теплоты обычно приходится разбивать рассматриваемый процесс на ряд элементарных процессов, каждый из которых соответствует весьма малому (в пределе — бесконечно малому) изменению параметров системы. Уравнение (1,5) для элементарного процесса имеет видQ= U+ A ,где Q элементарное количество теплоты, A — элементарная работа иU — приращение внутренней энергии системы в ходе данного элементарного процесса.

2-ое начало:

Второе начало термодинамики определяет условия, при которых возможны превращения одних видов энергии в другие, а также возможные направления протекания этих процессов. Потому как не все процессы, разрешенные I началом, возможны.

Формулировки II начала:

1. Клаузиус. Невозможен самопроизвольный переход тепла от менее нагретого тела к более нагретому, или невозможны процессы, единственным результатом

которых был бы переход тепла от менее нагретых тел к более нагретым.

2. Кельвин. Невозможны процессы, единственным конечным результатом

которых было бы превращение тепла целиком в работу.

Обе формулировки следуют одна из другой.

Второе начало запрещает существование перпетуум-мобиле 2-го рода (т.е. который превращал бы получаемое тепло целиком в работу). Причем второе начало по Кельвину можно перефразировать так: перпетуум-мобиле 2-го рода невозможен, или невозможно

создать тепловой двигатель с КПД η = 1. (Т.е. (A/Q) = 1).

3-ее начало:

Теорема Нернста гласит, что при стремлении абсолютной температуры к нулю энтропия любого тела также стремится к нулю:

lim S 0

T 0

И мы можем вычислить абсолютное значение энтропии по формуле

Отсюда следует, что при T 0 теплоемкость C p всех макросистем должна тоже стремиться к нулю (иначе интеграл не будет сходиться).

3. Средняя, среднеквадратичная и наиболее вероятная скорость молекулы

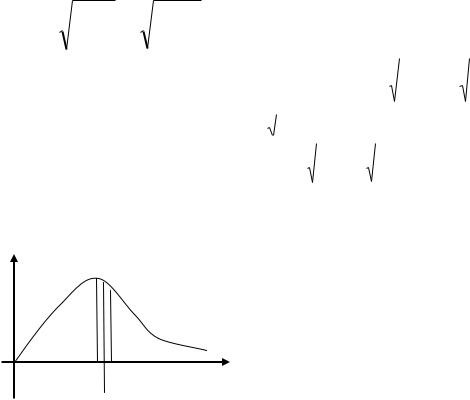
Наиболее вероятной скорости соответствует максимум функции распределения F(v). Эта скорость определяется из условия dF/dv=0, откуда следует

F(U )