3. Анализ трендовой модели прогнозирования показателей финансового развития ооо «Джошкуноз Алабуга» и эффективности управления финансовыми отношениями

Анализ трендовой модели прогнозирования показателей финансового развития позволяет оценить долгосрочное изменение финансовых показателей компании на основе их исторических данных.

Для временного ряда рентабельности продаж Rп построим трендовую модель в виде полинома первой степени:

Для этого полинома система нормальных уравнений имеет вид:

Чтобы найти параметры и составим таблицу 10.

Таблица 10

Расчет параметров модели для ООО «Джошкуноз Алабуга»

N/n	t
1	2	3	4	5	6	7
2	1	44,90	44,90	1	2015,99	42,32
3	2	26,44	52,87	4	698,84	35,80
4	3	40,25	120,74	9	1619,80	29,28
5	4	18,56	74,25	16	344,56	22,76
	10	130,15	292,76	30	4679,19	130,15

Подставляя полученные значения в систему уравнений, получим:

Умножив все члены первого уравнения на 2,5 (10/4), получим следующую систему уравнений:

Отнимем от первого уравнения второе. Отсюда –5а1 = 32,49. = – 6,5.

Таким образом, линейная модель в виде полинома первой степени выглядит следующим образом:

Необходимо проверить адекватность и точность построенной модели. Остаточная последовательность приведена в гр. 4 таблицы 11.

Таблица 11

Расчетные параметры модели для ООО «Джошкуноз Алабуга»

t	Фактическое yt	Расчетное Yt	Отклонение εt	Точки пиков	εt²	εt – εt-1	(εt – εt-1) ²	|εt| yt100
1	2	3	4	5	6	7	8	9
1	44,90	42,32	2,58	-	6,66	-	-	5,75
2	26,44	35,80	-9,36	1	87,57	-11,94	142,54	35,39
3	40,25	29,28	10,97	1	120,41	20,33	413,35	27,26
4	18,56	22,76	-4,20	-	17,61	-15,17	230,10	22,61
Σ	130,15	130,15	0,00		232,25		785,99	91,01

Как и в предыдущем параграфе, это будем проводить по четырем критериям.

Проверку случайности колебаний уровней остаточной последовательности, т.е. проверку гипотезы о правильности выбора вида тренда проведем на основе критерия пиков (поворотных точек). Их количество равно двум (р = 2). Количество пиков сравнивается с критическим ( ), которое, как и в предыдущем случае, равно 0, т.е. . Таким образом, гипотеза подтверждается.

Математическое ожидание случайной компоненты равно нулю, т.е. гипотеза о равенстве нулю математического ожидания случайной последовательности принимается.

Проведем проверку соответствия остаточной последовательности нормальному закону распределения. В этом случае размах вариации , а среднее квадратическое отклонение . Следовательно, критерий , и это значение попадает в интервал между верхней и нижней границами табличных значений данного критерия. Делаем вывод, что свойство нормальности распределения выполняется.

Для характеристики точности модели воспользуемся таким показателем, как среднее квадратическое отклонение, которое рассчитывается по формуле , что говорит о достаточном уровне точности построения модели.

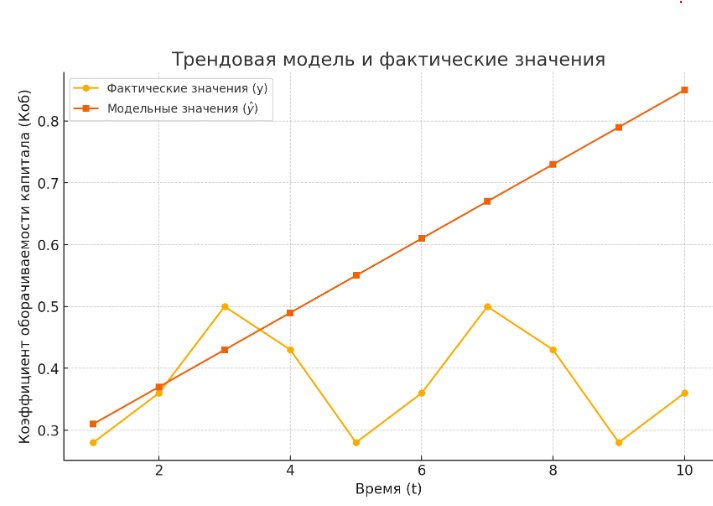
Рис.3 Трендовая модель