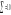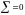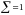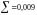- •Содержание
- •Введение
- •1. Характеристика и анализ финансовых показателей деятельности корпорации ооо «Джошкуноз Алабуга»
- •Технико-экономические показатели ооо «Джошкуноз Алабуга» за 2020 – 2022 гг.
- •Структура активов и пассивов баланса ооо «Джошкуноз Алабуга» за 2020 – 2022 гг.
- •Налоги, уплаченные ооо «Джошкуноз Алабуга»в 2021-2022 гг. [16]
- •Структура налогов ооо «Джошкуноз Алабуга»в 2021-2022 гг. [18]
- •Структура налоговой нагрузки ооо «Джошкуноз Алабуга»в зависимости от источника уплаты налогов и сборов в 2021-2022 гг. [12]
- •Аналитические коэффициенты налоговой нагрузки ооо «Джошкуноз Алабуга» в 2021-2022 гг. [19]
- •2.Корреляционный и регрессионный анализ показателей финансового состояния деятельности ооо «Джошкуноз Алабуга»
- •3. Анализ трендовой модели прогнозирования показателей финансового развития ооо «Джошкуноз Алабуга» и эффективности управления финансовыми отношениями
- •4.Оценка проблем управления финансовыми отношениями ооо «Джошкуноз Алабуга» и направления их решения
- •Выводы и предложения
- •Список использованной литературы
- •I. Нормативно-правовые материалы:
- •II. Специальная литература:
- •III. Интернет-ресурсы:
- •Приложение Приложение 1
2.Корреляционный и регрессионный анализ показателей финансового состояния деятельности ооо «Джошкуноз Алабуга»
Построим
трендовую модель в виде полинома первой
степени (линейная модель)
 для временного ряда коэффициента
оборачиваемости совокупного капитала
Коб.
для временного ряда коэффициента
оборачиваемости совокупного капитала
Коб.
Суть метода наименьших квадратов заключается в том, чтобы сумма квадратов отклонений фактических уравнений ряда от соответствующих выровненных по кривой роста значений была наименьшей, т.е.:
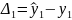
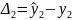
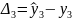

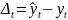
Критерием оптимальности считается минимальность сумм квадратов всех отклонений, т.е.:
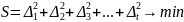
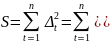
При


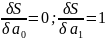
Решая последние два уравнения, найдем параметры модели:
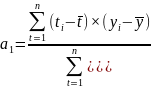 ;
;
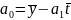 .
.
Чтобы
найти параметры
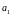 и
и
 составим
таблицу 7.
составим
таблицу 7.
Таблица 7
Расчет параметров модели для ООО «Джошкуноз Алабуга»
N/n |
t |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
2 |
1 |
0,28 |
-1,5 |
-0,11 |
0,16 |
2,25 |
0,31 |
3 |
2 |
0,36 |
-0,5 |
-0,04 |
0,02 |
0,25 |
0,36 |
4 |
3 |
0,50 |
0,5 |
0,11 |
0,05 |
0,25 |
0,42 |
5 |
4 |
0,43 |
1,5 |
0,04 |
0,06 |
2,25 |
0,48 |
6 |
5 |
0,28 |
-1,5 |
-0,11 |
0,16 |
2,25 |
0,31 |
7 |
6 |
0,36 |
-0,5 |
-0,04 |
0,02 |
0,25 |
0,36 |
8 |
7 |
0,50 |
0,5 |
0,11 |
0,05 |
0,25 |
0,42 |
9 |
8 |
0,43 |
1,5 |
0,04 |
0,06 |
2,25 |
0,48 |
10 |
9 |
0,28 |
-1,5 |
-0,11 |
0,16 |
2,25 |
0,31 |
|
10 |
1,58 |
|
|
0,29 |
5 |
1,58 |
Среднеарифметическое
значение
 =
2,5, а
=
2,5, а
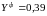 .
.
Отсюда получаем:
 ;
;
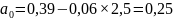

Требуется определить адекватность и точность построенной модели. Прежде всего, сформируем остаточную последовательность, для чего из фактических значений уровней ряда вычтем соответствующее расчетные значение по модели.
Таблица 8
Расчетные параметры модели для ООО «Джошкуноз Алабуга»
t |
|
|
Отклонение
|
Точки пиков |
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
0,28 |
0,31 |
-0,02 |
- |
0,0004 |
- |
- |
-7,41 |
2 |
0,36 |
0,36 |
0 |
- |
0 |
0,01 |
0,0001 |
2,03 |
3 |
0,50 |
0,42 |
0,08 |
1 |
0,0064 |
0,09 |
0,008 |
15,51 |
4 |
0,43 |
0,48 |
-0,05 |
- |
0,0025 |
-0,13 |
0,017 |
11,41 |
5 |
0,28 |
0,31 |
-0,02 |
- |
0,0004 |
- |
- |
-7,41 |
6 |
0,36 |
0,36 |
0 |
- |
0 |
0,01 |
0,0001 |
2,03 |
7 |
0,50 |
0,42 |
0,08 |
1 |
0,0064 |
0,09 |
0,008 |
15,51 |
8 |
0,43 |
0,48 |
-0,05 |
- |
0,0025 |
-0,13 |
0,017 |
11,41 |
9 |
0,28 |
0,31 |
-0,02 |
- |
0,0004 |
- |
- |
-7,41 |
10 |
0,36 |
0,36 |
0 |
- |
0 |
0,01 |
0,0001 |
2,03 |
|
|
|
|
|
|
|
Σ=0,02 |
|
Проверку будем, проводит по четырем признакам.
1.
Проверка случайности колебаний уровней
остаточной последовательности означает
проверку гипотезы о правильности выбора
вида тренда. Критерием для данной
проверки может служить критерий пиков
(поворотных точек). Уровень последовательности
 считается максимумом, если он больше
двух рядом стоящих уровней, т.е.
считается максимумом, если он больше
двух рядом стоящих уровней, т.е.
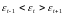 ,
и минимумом, если он меньше обоих соседних
уровней, т.е.
,
и минимумом, если он меньше обоих соседних
уровней, т.е.
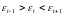 .
В обоих случаях
считается поворотной точкой; общее
число поворотных точек для остаточной
последовательности
обозначим через р.
.
В обоих случаях
считается поворотной точкой; общее
число поворотных точек для остаточной
последовательности
обозначим через р.
В
случайной выборке математическое
ожидание числа точек поворота
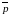 и дисперсии
и дисперсии
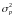 выражается формулами:
выражается формулами:
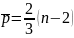 ;
;
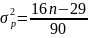
Критерием случайности с 5%-ным уровнем значимости, т.е. с доверительной вероятностью 95%, является выполнение неравенства
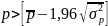 ,
,
где квадратные скобки означают целую часть числа.
Если это неравенство не выполняется, трендовая модель считается неадекватной.


Т.е. гипотеза о правильности выбора тренда подтверждается.
2. Проверка равенства математического ожидания случайной компоненты нулю, осуществляется на основе t-критерия Стьюдента. Расчетное значение этого критерия задается формулой:
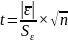 ,
где
,
где
 – среднеарифметическое
значение уровней остаточной
последовательности
по
модулю;
– среднеарифметическое
значение уровней остаточной
последовательности
по
модулю;
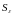 -
среднеквадратическое отклонение этой
последовательности.
-
среднеквадратическое отклонение этой
последовательности.
Из таблицы 2.7 видно (гр. 4), что сумма уровней остаточной последовательности равна 0, т.е. среднеарифметическое значение этого показателя также рано 0, значит расчетное значение t-критерия Стьюдента также равное нулю, меньше табличного, которое равно 1,05.
3. Проверка независимости значений уровней случайной компоненты (отсутствие автокорреляции) осуществляется по ряду критериев, наиболее распространенным из которых является d-критерий Дарбина-Уотсона. Расчетное значение этого критерия определяется по формуле:

Подставляя значение из таблицы 2.7 (гр. 8, гр. 6), получаем:

Эта
величина превышает 2, что свидетельствует
об отрицательной автокорреляции, поэтому
критерий Дарбина-Уотсона необходимо
преобразовать: Δd
= 4 – d
= 4 – 2,63 = 1,37. Данное значение сравнивается
с двумя критическими табличными
значениями критерия, которое для нашей
линейной модели можно принять равными
 и
и
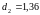 .
Т.к. расчетное значение критерия d
больше верхнего табличного значения
.
Т.к. расчетное значение критерия d
больше верхнего табличного значения
 ,
но меньше 2 то гипотеза о независимости
остаточной последовательности, т.е. об
отсутствии автокорреляции, принимается.
,
но меньше 2 то гипотеза о независимости
остаточной последовательности, т.е. об
отсутствии автокорреляции, принимается.
4. Проверка соответствия распределения случайной компоненты нормальному закону распределения может быть проведена, используя метод, основанный на RS-критерии. Этот критерий численно равен отношению размаха вариации случайной величины R к стандартному отклонению S:
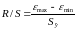 ,
где
,
где

Используя данные формулы, получаем:
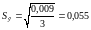

Вычисленное
значение сравнивается с интервалом из
таблицы, который равен
 ,
т.е. в данном случае вычисленное значение
попадает в табличный интервал, то
гипотеза о нормальном распределении
случайной компоненты подтверждается.
,
т.е. в данном случае вычисленное значение
попадает в табличный интервал, то
гипотеза о нормальном распределении
случайной компоненты подтверждается.
Таким образом, делается вывод об адекватности трендовой модели, т. к. все указанные выше четыре проверки свойств остаточной последовательности дали положительный результат.
После установления адекватности необходимо оценить точность данной трендовой модели. Точность модели характеризуется величиной отклонения выхода модели от реального значения моделируемой переменной (экономического показателя), при этом в качестве статистических показателей точности применим среднюю относительную ошибку аппроксимации, которая равна:

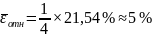 ,
,
т.к.
 ,
то это свидетельствует о высоком уровне
точности модели.
,
то это свидетельствует о высоком уровне
точности модели.
Для
данного временного ряда, дадим прогноз
на два шага вперед (t
= 5 и t
= 6) на основе адекватной линейной модели
 .
.
Точечные
прогнозы получим, подставляя в уравнение
модели значения
 и
и

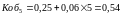
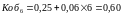
Для расчета доверительного интервала прогноза относительно линейного тренда применяют формулу:
 .
.
Здесь
t
– порядковый номер уровня ряда;
 =
n
+ L
– время, для которого делается прогноз;
=
n
+ L
– время, для которого делается прогноз;
 -
табличное значение критерия Стьюдента
для уровня значимости α;
-
табличное значение критерия Стьюдента
для уровня значимости α;
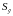 -
стандартная (средняя квадратичная)
ошибка оценки прогнозируемого показателя,
которая определяется по формуле:
-
стандартная (средняя квадратичная)
ошибка оценки прогнозируемого показателя,
которая определяется по формуле:
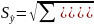 ,
,
При этом необходимо учесть, что в процессе оценки адекватности данной модели было найдено значение средней квадратичной ошибки оценки прогнозируемого показателя = 0,055.
Таким образом, формула расчета доверительного интервала для трендовых моделей отражает динамический аспект прогнозирования, т.е. увеличение неопределенности прогнозируемого процесса с ростом периода упреждения проявляется в постоянном расширении доверительного интервала.
Таблица 9
Расчет прогнозируемых параметров модели для ООО «Джошкуноз Алабуга»
Время (t) |
Шаг (L) |
Точечный прогноз (yn+L) |
Доверительный интервал |
|
Нижняя граница |
Верхняя граница |
|||
5 |
1 |
0,63 |
0,45 |
0,63 |
6 |
2 |
0,69 |
0,51 |
0,69 |
Так как модель, на основе которой осуществлялся прогноз, признана адекватной, то с принятым уровнем значимости 0,2, другими словами, с доверительной вероятностью 0,8 (80%) можно утверждать, что при сохранении сложившихся закономерностей развития прогнозируемая величина попадает в интервал, образованный нижней и верхней границами.

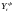
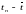

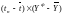

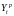
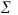

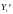
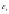



 х100
х100