ChislMetody_Lab4

Лабораторная работа 4.

Задание 1.

(При линейности остаточного члена)

function [ dy0_1, dy0_2 ] = derivate( y, x0, epsilon )

h_1=epsilon;

h_2=sqrt(epsilon);

dy0_1=(y(x0+h_1)-y(x0))/h_1;

dy0_2=(y(x0+h_2)-y(x0-h_2))/(2*h_2);

end

y=@(x) exp(2*x);

h1=10^(-3);

h2=10^(-6);

x0=1.5;

dy1_h1=derivate(y,x0,h1)

dy1_h2=derivate(y,x0,h2)

dy1_h1 = 40.2113

dy1_h2 = 40.1711

Задание 2.

y=@(x) exp(2*x);

i=[1:1:10];

h=2.^(-i);

x0=1.5;

etalon=derivate(y,x0,10^(-10));

for j=1:1:length(h)

[dy1(j),dy2(j)]=derivate(y,x0,h(j));

delta1(j)=abs(dy1(j)-etalon);

delta2(j)=abs(dy2(j)-etalon);

end

dy1

dy2

dy1 =69.0252 52.1197 45.6384 42.7897 41.4530 40.8053 40.4866 40.3284 40.2496 40.2103

dy2 = 54.9660 47.2091 43.6034 41.8659 41.0132 40.5908 40.3806 40.2758 40.2234 40.1972

Проверка:

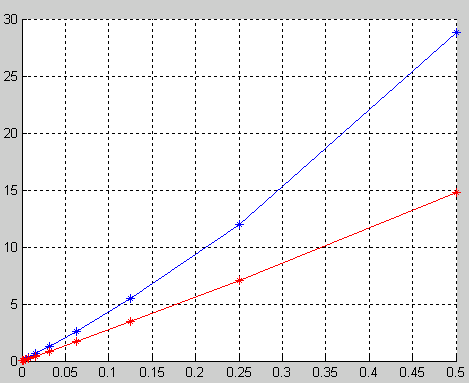
hold on

grid on

plot(h,delta1)

plot(h,delta1,'*')

plot(h,delta2,'Color','Red')

plot(h,delta2,'*','Color','Red')

fplot(@(x) 1/25*x^2,[0 1])

Задание 3.

Погрешность убывает не монотонно. Значащие цифры выходят за пределы мантиссы, приращение становится нулевым и численная производная равна нулю

hold on;

g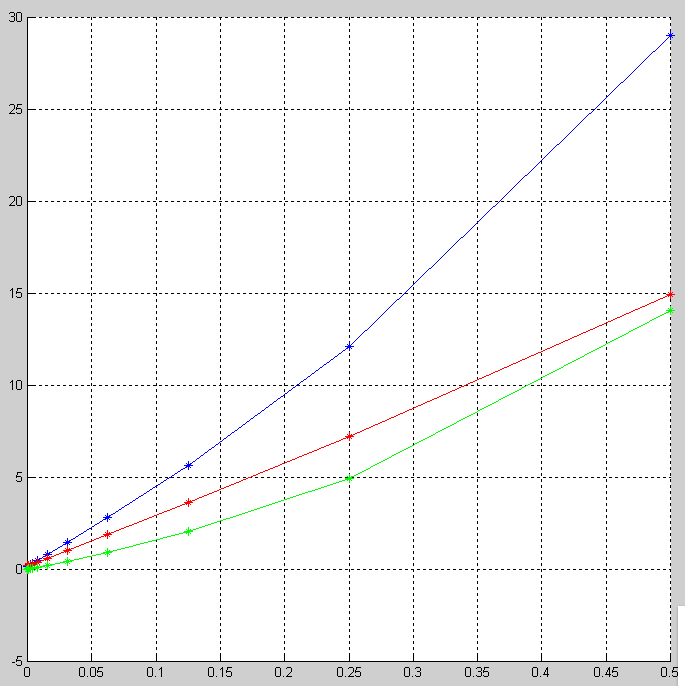 rid on;

axis square;

y=@(x) exp(2*x);

i=[1:1:400];

h=2.^(-i);

x0=1.5;

etalon=derivate(y,x0,10^(-10));

for j=1:1:length(h)

[dy1(j),dy2(j)]=derivate(y,x0,h(j));

delta1(j)=abs(dy1(j)-etalon);

delta2(j)=abs(dy2(j)-etalon);

end

dy1;

dy2;

dy3=dy1-dy2;

dy1=dy1-40;

dy2=dy2-40;

plot(h,dy1,'*','Color','Blue')

plot(h,dy1)

plot(h,dy2,'*','Color','Red')

plot(h,dy2,'Color','Red')

plot(h,dy3,'*','Color','Green')

plot(h,dy3,'Color','Green')

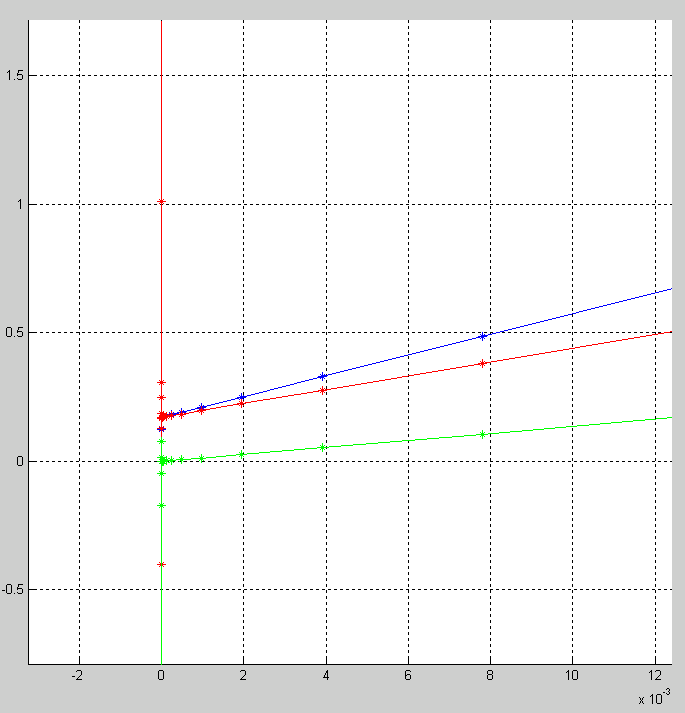
clc

clear all

close all

hold on;

grid on;

axis square;

y=@(x) exp(2*x);

i=[1:1:55];

h=2.^(-i);

x0=1.5;

etalon=derivate(y,x0,10^(-10));

for j=1:1:length(h)

[dy1(j),dy2(j)]=derivate(y,x0,h(j));

delta1(j)=abs(dy1(j)-etalon);

delta2(j)=abs(dy2(j)-etalon);

end

dy1;

dy2;

dy3=dy1-dy2;

dy1=log(abs(dy1-2*exp(3)));

dy2=log(abs(dy2-2*exp(3)));

h = log(h)

plot(h,dy1,'*','Color','Blue')

plot(h,dy1)

plot(h,dy2,'*','Color','Red')

plot(h,dy2,'Color','Red')