
Презентации лекций в одном файле
.pdf
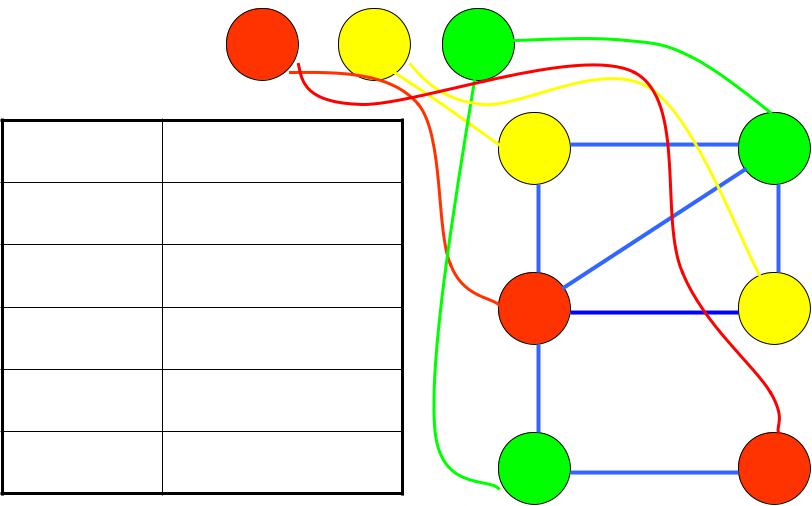
Раскраска графа – алгоритм Зыкова
M1= X- X2*X3*X4={X1,X5,X6}
M2= X - X1*X3*X4*X5 ={X2,X6}
M3= X - X1*X2*X3*X5 ={X4,X6}
M4= X - X2*X4*X6={X1,X3,X5}
M5= X - X1*X2*X5*X6 ={X3,X4}
Раскрасить граф – поставить в соответствие каждой вершине графа некоторый цвет так, чтобы смежные вершины были окрашены в разные цвета.
Запишем логическое выражение: каждая вершина может быть окрашена в один из цветов (ВУМ). Минимизируем это выражение. Наименьшее количество цветов – хроматическое число графа.
(М1+М4) *М2*(М4+М5) (М3+М5) (М1+М4) (М1+М2+М3)= (М1*М2 + М2*М4) * (М5+М3*М4)= М1*М2*М5+М2*М4*М5+М1*М2*М3*М4+М2*М3*М4=
М1*М2*М5+М2*М4*М5+М2*М3*М4
1 2 3 |C2|=3 (хроматическое число графа)
Решение задачи
(М1+М4) *М2*(М4+М5) (М3+М5) (М1+М4) (М1+М2+М3)
М2*М4*М5 М2 М4
Х1 М4
Х2 М2
Х3 М4 или М5
Х4 М5
Х5 М4
Х6 М2
М5 |
|
X1 |
X4 |
X2 |
X5 |
X3 |
X6 |
Задача о назначении. Венгерский алгоритм.
Пусть существуют несколько заданий (Job’s) и процессоров (Processor’s). Известно время выполнения каждого задания каждым процессором.
|
Job 1 |
Job 2 |
Job 3 |
Job 4 |
Job 5 |
|
|
|
|
|
|
Processor 1 |
2 |
1 |
6 |
∞ |
9 |
|
|
|
|
|
|
Processor 2 |
2 |
7 |
2 |
14 |
2 |
|
|
|
|
|
|
Processor 3 |
7 |
6 |
1 |
14 |
15 |
|
|
|
|
|
|
Processor 4 |
6 |
12 |
2 |
18 |
11 |
|
|
|
|
|
|
Processor 5 |
1 |
7 |
∞ |
2 |
7 |
|
|
|
|
|
|
Необходимо распределить задания между процессорами так, чтобы суммарное время выполнения было минимальным.
Это задача линейного назначения.
Будем решать задачу с помощью венгерского алгоритма. Процедура 1. Получение 0 в каждой строке и столбце матрицы.
|
Job 1 |
Job 2 |
Job 3 |
Job 4 |
Job 5 |
MIN |
|
|
|
|
|
|
|
Processor 1 |
2 |
1 |
6 |
∞ |
9 |
- 1 |
|
|
|
|
|
|
|
Processor 2 |
2 |
7 |
2 |
14 |
2 |
- 2 |
|
|
|
|
|
|
|
Processor 3 |
7 |
6 |
1 |
14 |
15 |
- 1 |
|
|
|
|
|
|
|
Processor 4 |
6 |
12 |
2 |
18 |
11 |
- 2 |
|
|
|
|
|
|
|
Processor 5 |
1 |
7 |
∞ |
2 |
7 |
- 1 |
|
|
|
|
|
|
|
Найдем минимальный элемент (MIN) в каждой строке и вычтем его из всех элементов строки.
Проверим, есть ли 0 в каждом столбце таблицы. Если нет, поступим аналогично строкам.
|
Job 1 |
Job 2 |
Job 3 |
Job 4 |
Job 5 |
|
|
|
|
|
|
Processor 1 |
1 |
0 |
5 |
∞ |
8 |
|
|
|
|
|
|
Processor 2 |
0 |
5 |
0 |
12 |
0 |
|
|
|
|
|
|
Processor 3 |
6 |
5 |
0 |
13 |
14 |
|
|
|
|
|
|
Processor 4 |
4 |
10 |
0 |
16 |
9 |
|
|
|
|
|
|
Processor 5 |
0 |
6 |
∞ |
1 |
6 |
|
|
|
|
|
|
MIN |
|
|
|
- 1 |
|
|
|
|
|
|
|
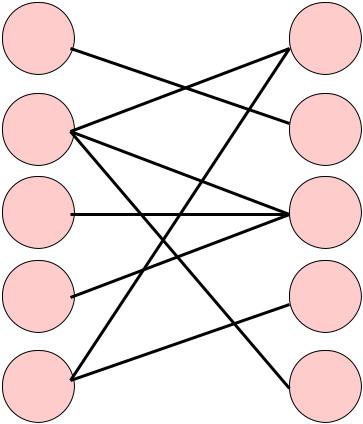
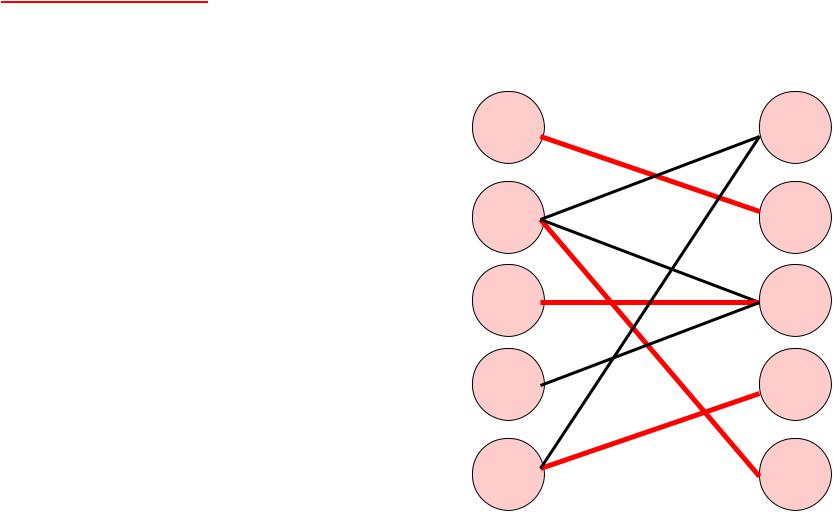
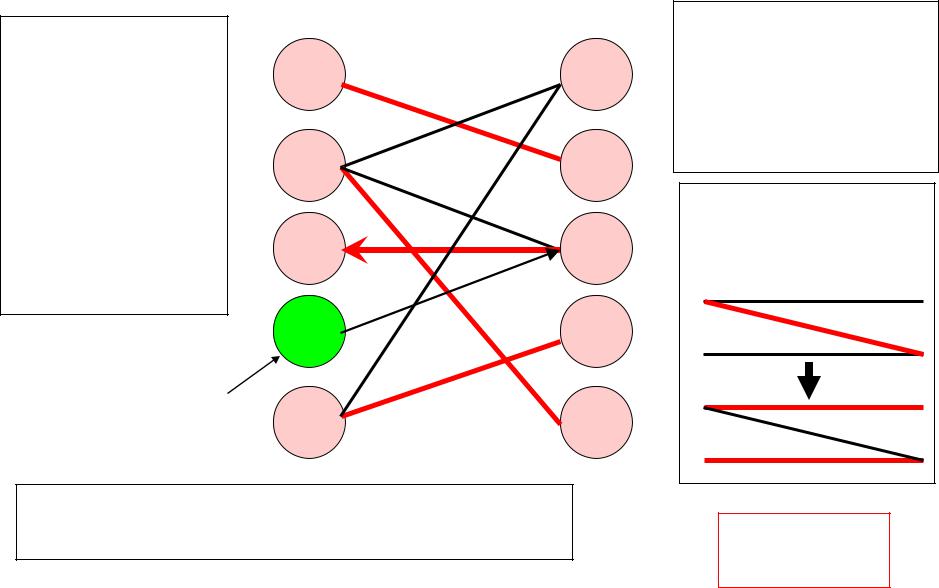
Процедура 4. Перестановка нулей. Найдем min опору графа. |
||||||
Опора: минимальное множество вершин, инцидентных всем дугам. |
||||||
Из «худой» |
|
|
|
|
Число вершин в |
|
|
|
|
|
минимальной опоре |
||
вершины идем |
|
X1 |
Y1 |
|
||
|
|
равно числу дуг в |
||||
вперед по |
|
|
|
|
||
|
|
|
|
максимальном |
||
«худым» дугам, |
|
|
|
|
||
|
|
|
|
паросочетании !!! |
||
назад по |
|
X2 |
Y2 |
|
||
|
|
|
||||
«жирным» и |
|
|
|
|
Если из «худой» вершины |
|
помечаем |
|
|
|
|
Х пришли в «худую» Y, то |
|
α |
X3 |
Y3 |
α |
делаем инверсию дуг |
||
вершины |
||||||
|
||||||
|
|
|
|
|
||
индексом α. |
|
|
|
|
|
|
|
α |
X4 |
Y4 |
|
|
|
«Худая» вершина |
|
|
|
|
|
|
|
|
X5 |
Y5 |
|
|
|
В опору войдут вершины Х не помеченные α и |
|
|
|
|||
вершины Y помеченные α. |
|
|
Опора: |
|||
|
|
|
|
|
X1,X2,X5,Y3 |
|
