
Презентации лекций в одном файле
.pdf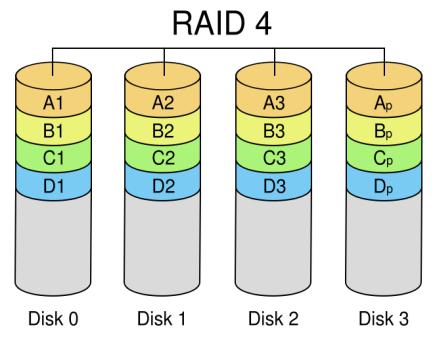
RAID 4
RAID 4 похож на RAID 3, но отличается от него тем, что данные разбиваются на блоки, а не на байты. Таким образом, удалось «победить» проблему низкой скорости передачи данных небольшого объема. Запись же производится медленно из-за того, что четность для блока генерируется при записи и записывается на единственный диск. Используются массивы такого типа очень редко.
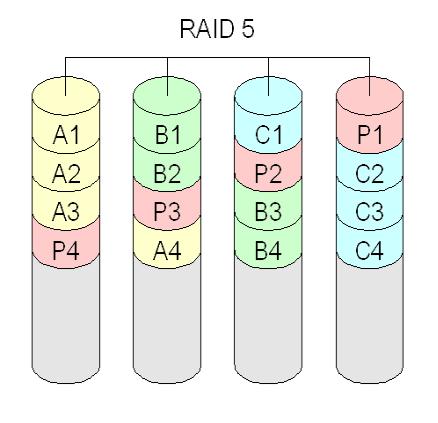
RAID 5
В RAID 5 данные и контрольные суммы записываются на все диски массива.
Экономичен, получаем защиту от выхода из строя любого из винчестеров тома. На запись информации на том RAID 5 тратятся дополнительные ресурсы, так как требуются дополнительные вычисления, зато при чтении имеется выигрыш, потоки данных с нескольких накопителей массива распараллеливаются. Недостатки RAID 5 - при выходе из строя одного из дисков — весь том переходит в “критический режим,, резко падает производительность. Если во время восстановления массива, вызванного выходом из строя одного диска, выйдет из строя второй диск — данные в массиве разрушаются. Минимальное количество используемых дисков равно трём.
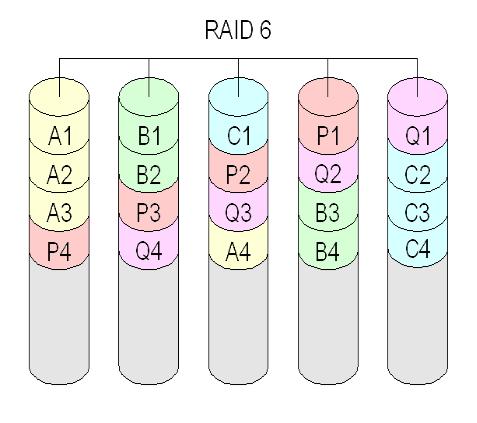
RAID 6
RAID 6 (Advanced Data Guarding) —
похож на RAID 5, но имеет более высокую степень надежности — под контрольные суммы выделяется емкость 2-х дисков, рассчитываются 2 суммы по разным алгоритмам. Требует более серьезный процессор контроллера — сложная материнская плата. Обеспечивает работоспособность после «смерти» одновременно 2-х дисков. Для организации массива требуется минимум 4 диска.
RAID 7
RAID 7 — зарегистрированная марка компании Storage Computer Corporation.
Структура массива такова: на n − 1 дисках хранятся данные, один диск используется для складирования блоков четности. Но добавилось несколько важных деталей, призванных ликвидировать главный недостаток массивов такого типа: кэш данных и быстрый контроллер, обрабатывающий запросы. Это позволило снизить количество обращений к дискам для вычисления контрольной суммы данных. В результате удалось значительно повысить скорость обработки данных (в пять и более раз).
Прибавились и новые недостатки: очень высокая стоимость реализации такого массива, сложность его обслуживания, необходимость в ИБП для предотвращения потери данных в кэш-памяти при перебоях питания.
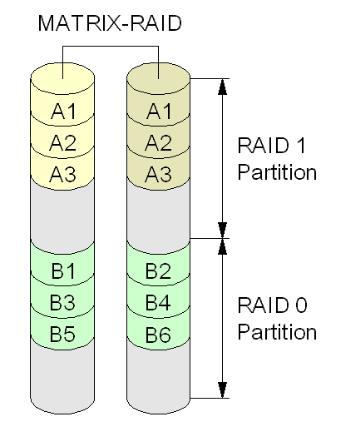
MATRIX RAID
Matrix RAID — это технология Intel. Не является новым уровнем RAID. Позволяет, используя лишь 2 диска, организовать одновременно один или несколько массивов уровня RAID 1 и один или несколько массивов уровня RAID 0. Это позволяет обеспечить для одних данных повышенную надёжность, а для других высокую скорость доступа.
Пример использования:
Имеются в наличии два диска по 160 Гбайт. Каждый диск разбивается на тома по 60 и по 100 Гбайт, затем 100-гигабайтные тома объединяются в скоростной массив RAID 0, а 60-гигабайтные — в массив повышенной надежности RAID 1. В массиве RAID 1 можно разместить операционную систему, а файл подкачки в массиве RAID 0. В результате получается сочетание повышенной производительности и надежности.
Пусть существуют несколько процессов, взаимодействующих по данным
ПРОЦЕСС |
ДАННЫЕ |
|
|
X1 |
A,C |
|
|
X2 |
A,B,D,E |
|
|
X3 |
B,F |
|
|
X4 |
C,D |
|
|
X5 |
D,E |
|
|
X6 |
F |
|
|
Как организовать их одновременную работу ?
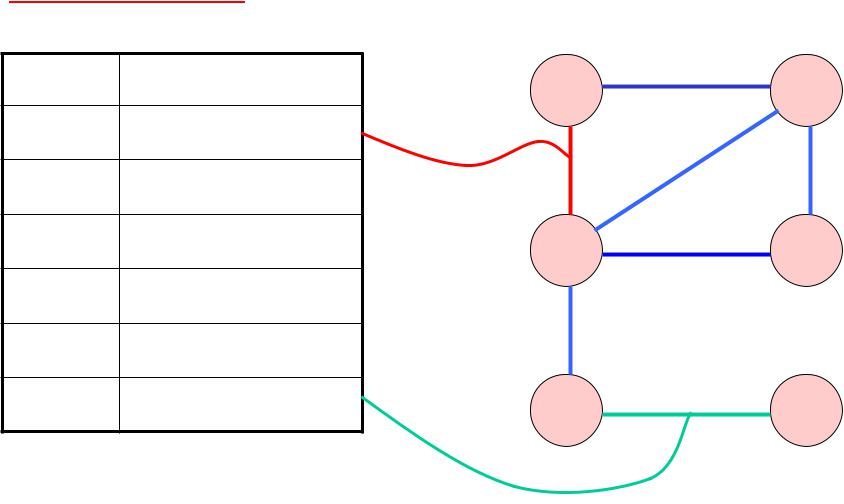
Чтобы найти процессы, конфликтующие по данным, построим граф.
Граф конфликтов: вершины – процессы, ребра общие данные.
ПРОЦЕСС |
ДАННЫЕ |
X1 |
X4 |
|
|
X1 A,C
X2 A,B,D,E
X3 |
B,F |
X2 |
X5 |
X4 C,D
X5 |
D,E |
|
|
X6 |
F |
X3 |
X6 |
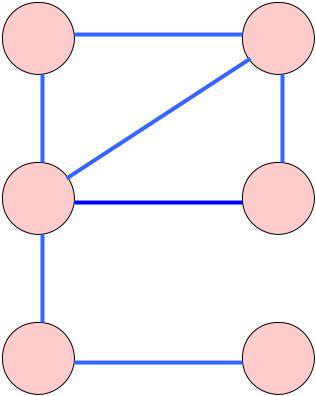
Один из подходов к решению задачи – нахождение внутренне устойчивых множеств и раскраска графа конфликтов.
X1 |
X4 |
X2 |
X5 |
X3 |
X6 |
Внутренне устойчивое множество (ВУМ) – подмножество несвязанных вершин графа (не имеющих общих ребер).
Максимальное ВУМ – ВУМ, которое теряет свойство внутренней устойчивости при добавлении любой вершины из оставшихся. Для нахождения ВУМ воспользуемся алгоритмом Магу.
Запишем логическое выражение: в ВУМ может войти либо одна, либо другая вершина каждого ребра. Минимизируем это выражение. Если полученные множества вершин исключить из множества всех вершин графа, то останется ВУМ.

Алгоритм Магу
(X1+X2) (X2+X3) (X1+X4) (X2+X4) (X2+X5) (X4+X5) (X3+X6)= (X2+X1*X3*X4*X5)(X4+X1*X5)(X3+X6)= (X2*X4+X1*X3*X4*X5+X1*X2*X5+ X1*X3*X4*X5)(X3+X6)=
(X2*X4+X1*X3*X4*X5+X1*X2*X5)(X3+X6)=
(X2*X3*X4+ X1*X3*X4*X5+ X1*X2*X3*X5 + X2*X4*X6 + X1*X3*X4*X5*X6 +X1*X2*X5*X6)=
X2*X3*X4+ X1*X3*X4*X5+ X1*X2*X3*X5 + X2*X4*X6 + X1*X2*X5*X6
ПОМОЩЬ: X*X=X, X+X=X, X1+X1*X2=X1,
(X1+X2)(X1+X3)=X1+X2*X3
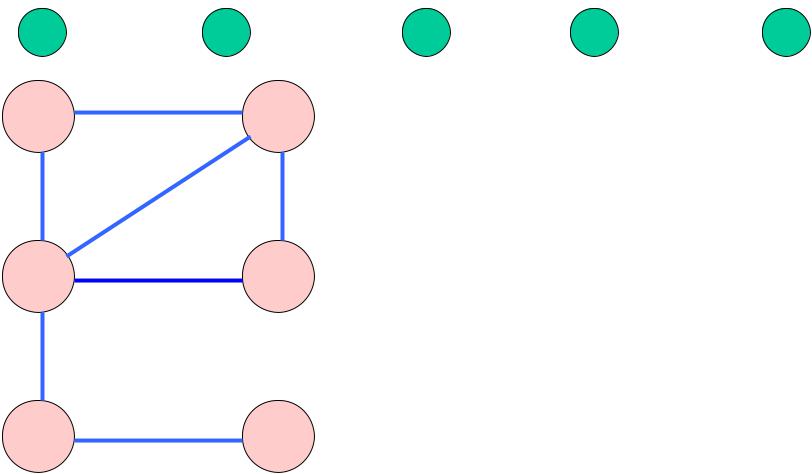
ВУМ
X2*X3*X4+ X1*X3*X4*X5+ X1*X2*X3*X5 + X2*X4*X6 + X1*X2*X5*X6
1 |
2 |
|
3 |
4 |
5 |
X1 |
|
X4 |
M1= X- X2*X3*X4={X1,X5,X6} |
|
|
|
|
|
|
||
M2= X - X1*X3*X4*X5 ={X2,X6}
X2 |
X5 |
M3= |
|
M4=
X
X
-X1*X2*X3*X5 ={X4,X6}
-X2*X4*X6={X1,X3,X5}
X3 |
X6 M5= X - X1*X2*X5*X6 ={X3,X4} |
|M1|=|M4|=3 число внутренней устойчивости Входящие в ВУМ вершины не конфликтуют по данным!!!
