
Mathcad - Лабораторная работа МО - 1 в MathCAD
.pdf
"Метод дихотомии."
найти min функции |
|
|
|
F(x) := x2 + 8x - 10 |
|
|
||||||
Интервал неопределенности: |
A := -10.0 |
B := 2.0 |
|
|
||||||||
Точность вычислений: |
|
|
e := 0.001 |
|
|
δ := 0.0001 |
||||||
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) |
|
|
100 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
− |
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
− |
5 |
|
|
0 |
5 |
10 |
|||||
|
|
|
|
|
|
− 50 |
|
|
|
|
|
|
|
|
|
|
x := 0 |
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
Экстремум, |
Given |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
найденный |
|
x ³ -10 |
|
|
|
x £ 2 |
|
|
|
|||
встроенной |
Minimize(F, x) = -4 |
|
функцией: |
||
|
||
Dihotom(A, B , δ) := i ¬ 0 |
||
0 |
A |
|
M |
¬ |
|
|
B |
|
while 1
C ¬ (B - A) + A 2
λ ¬ C - δ μ ¬ C + δ
B ¬ if (F(λ) £ F(μ) , μ, B) A ¬ if (F(λ) > F(μ) , λ, A) i ¬ i + 1
i ¬ A
M B
break if B - A < e M 0 ¬ stack(M 0 , i)
M
Result := Dihotom(A, B , δ)
|
|
0 |
1 |
2 |
|
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
|
|
Result = |
0 |
-10 |
-10 |
|
-7 |
-5.5 |
-4.75 |
-4.375 |
-4.188 |
-4.094 |
1 |
2 |
-4 |
|
-4 |
-4 |
-4 |
-4 |
-4 |
-4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
14 |
0 |
|
0 |
0 |
0 |
0 |
0 |
... |
|
|
|
|
|
|
|
|
|
|
|
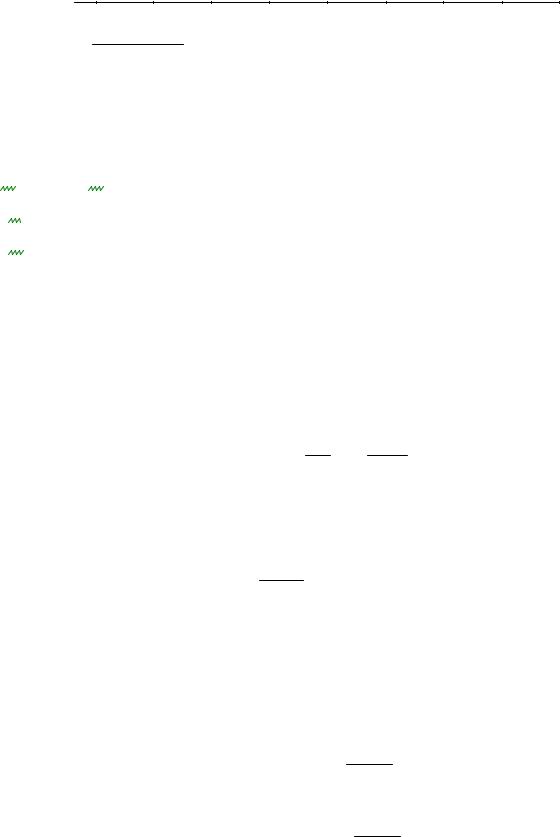
Xmin := [( -4.001 ) + -4] = ( -4.001 )
2
"Метод Фибоначчи."
Задание: найти min функции
A := -10 |
B := 2 |
e := 0.001
N := 17
k := 2 .. N + 1
|
|
0 |
|
|
|
|
0 |
1 |
|
|
|
|
1 |
1 |
|
|
|
|
2 |
2 |
|
|
|
|
3 |
3 |
|
|
|
|
4 |
5 |
|
|
|
|
5 |
8 |
|
|
|
|
6 |
13 |
FF = |
|
|
7 |
21 |
|
|
|
|
|
8 |
34 |
|
|
|
|
9 |
55 |
|
|
|
|
10 |
89 |
|
|
|
|
11 |
144 |
|
|
|
|
12 |
233 |
|
|
|
|
13 |
377 |
|
|
|
|
14 |
610 |
|
|
|
|
15 |
... |
|
|
|
Интервал неопределенности Точность вычислений
Количество вычислений
FF0 := 1 FF1 := 1
FFk := FFk−1 + FFk−2
Числа Фибоначчи
δn = δ1 + ε Fn−2
Fn Fn
(B - A) = 4.644 ´ 10− 3 FFN
λ ¬ A + FFN−i−1 × (B - A) FFN−i+1
μ ¬ A + FFN−i × (B - A) FFN−i+1
