
Lekcii_po_TekhnichTermodinamike
.pdf
15
ср см. = g1 ср 1 + g2 ср 2 + … + gn ср n . (2.24) сv см. = g1 ср 1 + g2 сv 2 + … + gn сv n . (2.25)
Удельные молярные (молекулярные) теплоемкости смеси:
срμ см. = r1 срμ 1 + r2 срμ 2 + … + rn срμ n . (2.26) сvμ см. = r1 сvμ 1 + r2 сvμ 2 + … + rn сvμ n . (2.27)
Теплоемкость газовых смесей
Теплоемкостью называется количество тепла, которое необходимо сообщить телу, чтобы повысить его температуру на 1 К.
Обычно теплоемкость относят к единице количества вещества, и в зависимости от этого различают:
удельную массовую теплоемкость с, отнесѐнную к 1кг газа, Дж/(кг К); удельную объѐмную теплоемкость с , отнесѐнную к 1м3 при нормальных
физических условиях, Дж/(м3 К); удельную мольную теплоемкость с, отнесѐнную к одному кмолю,
Дж/(кмоль К).
Зависимость между ними:
c = с/ ; с = с н. ( н - плотность газа при НФУ).
= с н. ( н - плотность газа при НФУ).
Математическое выражение для удельной теплоѐмкости записывается следующим образом:
если при температуре Т сообщить 1кг газа бесконечно малое количество тепла dq, то температура газа изменится на dT, и тогда с = dq/dT, или: dq = c dT - основное уравнение теплоты в дифференциальном виде.
Теплоемкость однородного газа зависит от следующих факторов: природы газа; характера процесса; температуры.
Рассмотрим влияние этих факторов.
Чем сложнее газ, чем выше его молярная масса, чем выше степень связи у его молекул, тем выше его теплоемкость. Более полные сведения об этом можно найти в молекулярно-кинетической теории.
Теплоемкость является функцией процесса, т.е. зависит от характера подвода тепла. Это означает, что одно и то же рабочее тело в зависимости от процесса требует для своего нагревания на 1К различного количества теплоты.
Численная величина теплоемкости меняется от |
до |
. |
|||
В термодинамических расчѐтах большое значение имеют: |
|||||
теплоемкость при постоянном давлении |
|
|
|||
cр |
dq |
|
и |
|
|
|
|
|
|
||
dT |
|
|
|||
|
|
p const |
|
|
|
теплоемкость при постоянном объѐме |
|
|
|||
cv |
dq |
|
. |
|
|
|
|
|
|
||
dT |
|
|
|
||
|
|
v const |
|
|
|
Между этими теплоемкостями выполняется уравнение Майера (дается без вывода):

16
сp - cv = R, или сp - cv = 8314 Дж/(кмоль К.)
Из соотношения Майера сp=cv+R видно, что сp > cv (R — величина положительная) на величину R. Дело в том, что в процессе V = const теплота, сообщаемая газу, идѐт лишь на изменение его внутренней энергии, тогда как в процессе р = const теплота расходуется и на увеличение внутренней энергии, и на совершение работы против внешних сил (R - работа).
Если повышать температуру газа путем его сжатия, не подводя и не отнимая тепло, то процесс называется адиабатным и его теплоемкость с=0:
dq = 0, т.е. dq = cdT = 0, c = dq/dT = 0.
При изотермическом процессе Т = const, dT = 0 и dq = 0, т.к. dq = cdT = 0, c = dq/dT = 0/0 =  .
.
Отношение ср/cv = k — показатель адиабаты. Показатель адиабаты k зависит от количества атомов в молекуле газа. Для двухатомных газов (и воздуха) k = 1,4; для одноатомных газов k = 1,67; для трехатомных k = 1,33.
Опыты показывают, что при повышении температуры газа колебательные движения атомов в молекуле усиливаются, на что расходуется всѐ большее и большее количество энергии. Следовательно, чем выше температура, тем больше теплоты приходится расходовать для нагревания газа на 1 , т.е. теплоемкость возрастает с ростом температуры.
В общем случае теплоемкость с в зависимости от t может быть
представлена в виде:
c = со+аt+bt2+dt3+...,
где со - теплоемкость при 0 С;
а,b,d — постоянные коэффициенты.
В технических расчетах можно применять линейные зависимости, т.к. коэффициенты b,d - весьма малы :
c = со+аt,
На графике представлены две зависимости: полином n-ой степени и линейная.
C
c=c0+at
c=c0+at+bt2
t
Рис. 1.2. зависимость истинной теплоемкости от температуры
Поскольку теплоемкость зависит от температуры, в термодинамике различают истинную и среднюю теплоемкости.
Средней теплоемкостью сср данного процесса в интервале температур от t1 до t2 называется отношение количества теплоты, сообщаемое газу, к разности конечной и начальной температур:
c– р |
t2 |
|
|
q |
|
. |
t |
t |
|
|
|
||
|
2 |
|
t |
|||
|
1 |
|
|
1 |
|
|
Выражение с = dq/dT - определяет теплоемкость при данной температуре или так называемую истинную теплоемкость.
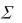
17
На теплоемкость газовой смеси влияет еѐ состав, поэтому при массовом задании смеси еѐ теплоемкость :
c =с1g1 + c2g2 + c3g3 +...cngn = cigi.
где ci - теплоемкости компонентов; gi - массовые доли компонентов.
Более подробные сведения относятся к самостоятельному изучению материала для расчетного задания ―Газовые смеси и теплоемкость‖.
18
ЛЕКЦИЯ 4
Работа и рабочая диаграмма
|
|
|
|
Рассмотрим процесс изменения состояния |
|
|
|
|
|
||
F |
|
|
|
1кг газа |
в цилиндре с подвижным поршнем, |
|
P |
dh |
двигающимся без трения; давление окружающей |
||
|
среды р, площадь поршня F. Подведѐм к |
||||
|
|
||||
|
|
|
|
||
|
|
|
|
цилиндру тепло q; газ нагреется, расширится и |
|
|
|
|
|
||
|
1 кг |
|
|
сдвинет поршень на высоту dh. |
|
|
раб. тела |
|
|
Тогда элементарная работа, совершаемая газом, |
|
|
|
|
|
против сил давления, равна: |
|
|
q |
|
|
dl |
p F d h pdv. |
Таким образом, элементарная работа равна произведению давления газа на изменения его объема dl = pdv. Работу, совершаемую при расширении газа, называют также технической.
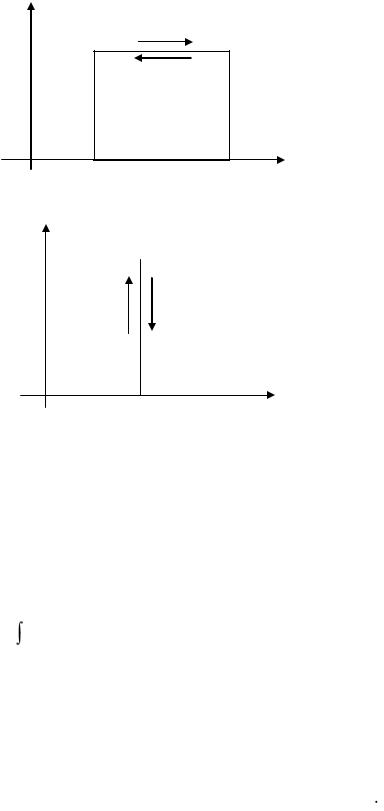
Для графического определения работы удобно пользоваться диаграммой, по которой на оси абсцисс откладывается значение удельного объема газа v, по оси ординат - установившееся при этом давление.
P |
|
|
|
P1 |
1 |
|
|
|
|
|
|
p |
|
|
|
|
|
|
2 |
P2 |
|
|
|
V1 |
dv |
V2 |
V |
Рис 1.4. Графическое изображение работы в p,v |
|||
координатах |
|
|
|
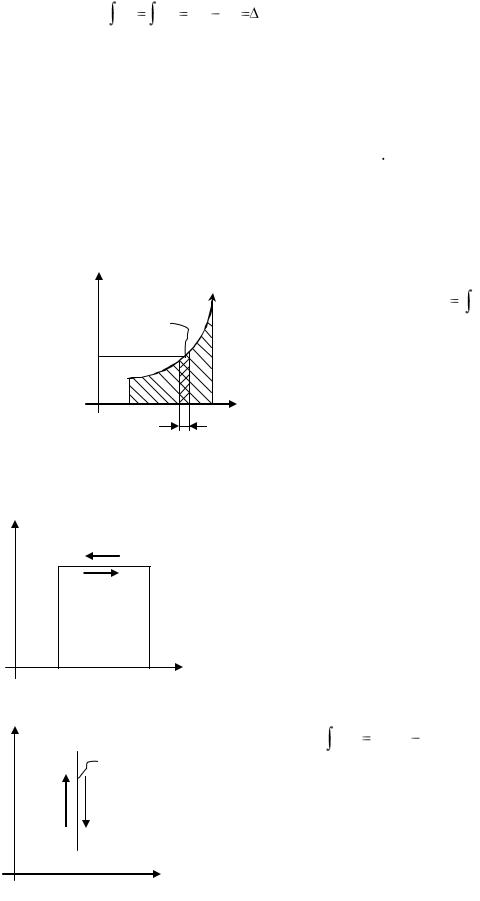
Линия 1-2 характеризует процесс расширения газа; выделим элементарный участок, где р = const, с основанием dv. Тогда выражение pdv представляет элементарную работу dl: pdv = dl, а графически - это площадь элементарного участка. Для нахождения всей работы в процессе 1-2 надо взять интеграл:
v2
l  pdv .
pdv .
v1
Графически работа будет равна площади фигуры v1-1-2-v2. Для численного нахождения работы надо знать зависимость p(v), т.е. подинтегральную функцию, или надо знать характер процесса, а не только начальные и конечные точки 1 и 2.
19
Работа при увеличении объѐма газа принимается за положительную, при сжатии работа отрицательная.
Рассмотрим некоторые примеры.
P
1 |
2 |
L
V1 |
|
V2 |
|
V |
|
|
|
|
|
|
а) |
V |
1 |
|
2
V1=V2 |
V |
|
|
б) |
|
Рис.1.5. Определение работы изобарного (а) и изохорного (б) процесса
Р= const - изобарный процесс расширения (1-2) или сжатия (2-1):
v2
l  pdv =р(v2-v1)
pdv =р(v2-v1)
v1
Работа процесса 1-2 положительная, процесса 2-1 - отрицательная.
V=const - изохорный процесс; dv=0;
dl=pdv=0 - работа не совершается.
В системе Си работа измеряется в Дж: 1Дж=1Н м.

20
Внутренняя энергия и теплота
Молекулы газообразного рабочего тела находятся в постоянном хаотичном движении. Внутренняя энергия состоит из кинетической энергии поступательного, вращательного и колебательного движения молекул, потенциальной энергией взаимодействия молекул, энергии внутриатомных и внутриядерных движений частиц, из которых состоят атомы и др.
Внутренняя кинетическая энергия является функцией температуры:
Uкин= f(T).
Между молекулами реального газа существуют силы взаимодействия. Эти силы определяют по потенциальной энергии:
Uпот= f(р,v).
Тогда полная энергия:
U= Uкин+ Uпот=f(р,v,T).
Таким образом, полная внутренняя энергия систем является функцией основных параметров состояния, т.е. является функцией состояния.
В идеальном газе силы сцепления между молекулами отсутствуют, т.е. для идеального газа внутренняя энергия является функцией только температуры:
U = f(T).
Для идеального газа: dU = cv dT (формула даѐтся без вывода)
Техническое определение внутренней энергии. Внутренняя энергия -
это тепловой параметр состояния, численно равный теплу, которое нужно сообщить 1кг газа, чтобы повысить его температуру от условного 0 (для газа обычно 0 С) до заданной температуры в процессе V=const.
Внутренняя энергия может переходить в другие виды энергии или передаваться от тела с большим еѐ запасом к телу с меньшим запасом, в последнем случае она проявляется в виде теплоты.
Теплота - это форма проявления внутренней энергии, результат процесса. Внутренняя энергия - функция состояния рабочего тела.
Единицы измерения теплоты, внутренней энергии такие же, как работы - Джоуль. В случае удельных величин - Дж/кг.
|
|
Энтальпия |
|
Одной |
из |
энергетических характеристик термодинамической системы |
|
|
|
является тепловая функция, или энтальпия. Энтальпию |
|
P=p*F |
|
называют вторым тепловым параметром состояния |
|
F |
|
(первый параметр - внутренняя энергия). |
|
|
|
Рассмотрим полную энергию системы, состоящей |
|
|
|
из рабочего тела (газа) и поршня с грузом: |
|
1 кг. |
h |
она состоит из внутренней энергии рабочего тела |
|
U и потенциальной энергии поршня с грузом: |
|||
раб. т. |
|
||
|
|
U+pFh=U+pv=i. |
|
Рис. 1.6. К определению |
|||
физического |
смысла |
||
энтальпии. |
|
|
|
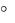
21
Это выражение обозначим через i и назовѐм энтальпией. Энтальпия представляет сумму внутренней энергии системы и произведение давления системы р на объѐм v. Единица измерения удельной энтальпии Дж/кг.
Энтальпией удобно пользоваться в тех случаях, когда в качестве независимых переменных выбирают давление р и температуру.
Для идеального газа:
рV=RT, di=dU+d(pV)=dU+RdT=CvdT+RdT=(Cv+R)dT= CpdT .
Таким образом di= CpdT.
Техническое определение энтальпии: энтальпия - это тепловой параметр состояния рабочего тела, численно равный теплу, которое необходимо сообщить 1кг, чтобы повысить его температуру от условного 0 (для газов, обычно 0 С) до заданной в процессе р = const.
Обратимые и необратимые процессы
Обратимыми называются процессы, которые могут протекать в прямом и обратном направлении, не вызывая изменений в окружающей среде, т.е. в обратимых процессах газ последовательно проходит ряд состояний, возвращаясь в исходное без изменений во внешней среде.
В природе обратимых процессов нет, это абстрактное понятие. Все реальные процессы необратимы, они сопровождаются трением, необратимой диссипацией энергии. Однако понятие обратимости даѐт возможность рассмотреть многие закономерности в термодинамике и вывести ряд важных уравнений. В дальнейшем вводятся поправки на необратимость.
22
ЛЕКЦИЯ 5
Первый закон термодинамики
Вприроде существует множество различных видов энергии (кинетическая, электрическая, внутренняя и т.д.), качественно отличающихся друг от друга. Энергия одного вида в результате взаимодействия тел может превращаться или переходить в любой другой вид энергии, причем в
изолированной системе сумма всех видов энергии остается постоянной.
Вчисле первых ученых, утверждавших принцип сохранения материи и энергии, был М.В. Ломоносов. В своем знаменитом письме к Эйлеру он писал: ―Все перемены, в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимается, столько же присовокупляется к другому. Так, ежели где убудет несколько материи, то умножится в другом месте. Сей всеобщий естественный закон простирается и в самые правила движения. Ибо тело, движущее своей силой другое, столько же оные у себя теряет, сколько сообщает другому, которое от него движение получает.‖
Первый закон (первое начало) термодинамики представляет собой частный случай всеобщего закона сохранения и превращения энергии применительно к тепловым явлениям. Он утверждает, что энергия не исчезает
ине возникает вновь, она лишь переходит из одной формы в другую.
Пусть телу произвольной массы сообщается тепло dQ, при этом происходит следующее:
изменится внутренняя кинетическая энергия dUкин; изменится внутренняя потенциальная энергия dUпот; изменится внешняя энергия системы
|
Mw2 |
||
d |
|
d (gMh), |
|
2 |
|||
|
|
||
где первый член — изменение внешней кинетической энергии, второй — внешней потенциальной.
Кроме, того рабочее тело может совершать работу против внешних сил
dLвнеш.
Уравнение баланса энергии:
dQ dU |
|
|
dU |
|
|
d |
Mw2 |
d (Mgh) dL . |
|
|
|
2 |
|||||
|
|
внеш |
||||||
|
кин |
|
|
пот |
|
|
||
|
|
du |
|
|
|
|
|
|
Для идеального газа d(Mgh) = 0, для относительно неподвижного |
||||||||
рабочего тела d |
|
Mw 2 |
|
0, |
|
|
||
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||
тогда:
dQ=dU+dLвнеш, или для 1кг рабочего тела:
dq=du+dl — тепло, подводимое к рабочему телу, частично идет на
изменение его внутренней энергии, частично — на совершение работы против внешних сил.

23
Полученное выражение является математическим выражением первого закона термодинамики. Каждый из трех членов этого уравнения может быть положительным, отрицательным или равным 0.
Если тепло сообщается рабочему телу, то dq>0, если отнимается - dq<0. Рассмотрим некоторые модификации этого уравнения.
dq=du+pdv,
где dl=pdv — работа расширения или сжатия. Для идеального газа:
dq=cvdT+pdv.
Продифференцируем выражение для энтальпии газа i = u + pv: di=du+pdv+vdp, но т.к. du+pdv=dq, то di=dq+vdp, или: dq=di-vdp.
Проанализируем первый закон с математической точки зрения: dq=du+dl.
du - полный дифференциал, т.к. внутренняя энергия является функцией состояния. Элементарная работа dl - не является полным дифференциалом, т.к. работа зависит от процесса, а не от состояния. Следовательно, их сумма dq не является полным дифференциалом, т.е. тепло участвующее в процессе, зависит от характера процесса.
Первый закон термодинамики дает количественное соотношение между теплом, работой и внутренней энергией.
Второй закон термодинамики. Энтропия
Немецким ученым Рудольфом Клаузиусом в 1854 году при исследовании условий превращения тепла в работу была введена в термодинамику специальная математическая функция, названная им энтропией, что означает в переводе с греческого tropos - превращение или преобразование.
Рассмотрим в
P
1
dq
2
p,v координатах произвольный обратимый процесс 1-2 изменения состояния газа.
Разобьем весь процесс на бесконечно большое число бесконечно малых отрезков и будем считать, что температура рабочего тела на каждом элементарном участке процесса в виду его малости остается неизменной. Для каждого участка отношение бесконечно малого количества тепла dq, подводимого к рабочему телу на этом участке, к постоянной
|
|
|
температуре T, при которой это тепло подведено, dq |
|
|
|
|
||
|
V |
|
T |
|
|
— тоже |
представляет собой бесконечно малую |
||
|
|
|
||
|
|
|
||
Рис. 1.7. К определению |
|
|||
|
величину, обозначенную через ds, т.е. dqT = ds. |
|||
понятия энтропии |
|
|||
|
|
|
Для |
процесса 1-2 можно это уравнение |
проинтегрировать:
|
|
|
|
|
|
24 |
2 |
2 |
dq |
|
|
|
S — изменение энтропии. |
dS |
|
|
S |
2 |
S1 |
|
|
T |
|||||
1 |
1 |
|
|
|
|
Чаще всего эта запись представляется в виде:
dq=TdS — аналитическая форма записи второго закона термодинамики.
Энтропия представляет собой некоторую однозначную функцию состояния рабочего тела, принимающую для каждого состояния вполне определенное значение, это третий тепловой параметр состояния. Единица изменения удельной энтропии — Дж/(кг К).
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов T, S - диаграмму, на которой (как и на p, v - диаграмме) состояние системы изображается точкой, а равновесный термодинамический процесс — линией. Изобразим произвольный процесс 1-2.
Из уравнения следует:
T |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
dq |
|
|
|
|
dq=TdS, q |
|
TdS. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Очевидно, |
что |
в |
T, |
S |
диаграмме |
||||
T |
1 |
|
q |
|
элементарная |
теплота |
|
процесса |
dq |
|||||||
|
|
|
изображается |
элементарной |
площадкой |
с |
||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||
|
|
|
dS |
|
основанием |
dS |
и высотой T, а площадь, |
|||||||||
|
|
|
S |
ограниченная |
линией |
процесса, |
крайними |
|||||||||
Рис. 1.8. Графическое изображение |
ординатами, |
и |
осью |
абсцисс, эквивалентна |
||||||||||||
теплоты в T,S – координатах |
теплоте процесса q. |
|
|
|
|
|
||||||||||
|
Вот почему |
изображение |
в |
T, |
S |
координатах называют тепловой |
||||||||||
|
|
|
|
диаграммой по аналогии с рабочей диаграммой в p, v |
||||||||||||
T |
|
|
|
координатах (там площадь эквивалентна работе). |
|
|||||||||||
1 |
|
2 |
|
Математическая |
запись |
|
второго |
закона |
||||||||
|
|
|
|
показывает, что dq и dS имеют одинаковые знаки. При |
||||||||||||
|
|
|
|
подводе |
теплоты |
dq>0, |
и |
энтропия |
тела |
возрастает |
||||||
|
|
|
|
(dS>0), а при отводе теплоты (dq<0) — убывает (dS<0). |
||||||||||||
|
|
|
|
Для того, чтобы вычислить тепло q, надо знать вид |
||||||||||||
|
|
|
|
зависимости T(S), т.е. знать характер процесса. |
|
|||||||||||
S1 |
|
S2 |
S |
Рассмотрим 2 примера. |
|
|
|
|
|
|||||||
|
Изотермический процесс T = const. |
|
|
|||||||||||||
|
а) |
|
|
|
|
|||||||||||
S 1
S=const
2
б) S
Рис. 1.9. Изображение изотермического (а) и адиабатного (б) процессов в T,S - координатах
S2
q  TdS T (S 2 S1 ) .
TdS T (S 2 S1 ) .
S1 1
Процесс может идти слева направо и наоборот.
Применим к этому процессу I закон термодинамики: dq=cvdT+pdv, но т.к. T=const, то dT=0, и dq=pdv — все тепло идет на совершение работы. Если процесс идет слева направо — увеличение объема, работа pdv>0; если уменьшение объема, то работа
