Определение реакций в подшипниках

Определение реакций в подшипниках

1. Ведущий вал (червяк)

Дано:

Ft1 = 934,6 H;

Fr1 = 612,34 H;

Fa1 = 1700,95 H;

Fм. = Н

LБ = 390 мм; d1 = 100 мм

LМ = 85 мм;

На рис. 1 составляем расчетную схему вала, проставляем все действующие на вал силы и определяем реакции опор:

1. Вертикальная плоскость

а) определяем опорные реакции

∑ М3 = 0 – Fr1 · – RАУ ·LБ + F_а1 = 0

RАУ =

∑ М1 = 0 Fr1 · – RВУ ·LБ + F_а1 = 0

RВУ =

Проверка: –RАУ + RВУ – Fr1 = –(– 88,1) + 524,2 – 612,34 = 0

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1…3, Нм

Мх1 = 0; Мх2 = RАУ · = – 88,1 · = – 17179,5 Н·мм = – 17,2 Н·м;

Мх3 = 0 Мх2 = RВУ · = 524,2 · = 102219 Н·мм = 102,2 Н·м;

1. Горизонтальная плоскость

а) определяем опорные реакции

∑ М3 = 0 Ft1 ·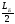 – RАX ·LБ + F_м ·LМ = 0

RАХ =

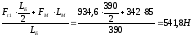
∑ М1 = 0 –Ft1 · – RВX ·LБ + F_м ·(LМ + LБ) = 0

RВХ =

Проверка: RАX – RВХ – Ft1 + F_м = 541,8 –(– 50,8) – 934,6 + 342 = 0

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1…4, Нм

Му1 = 0 Му2 = – RАХ · = – 541,8 · = – 105651Н·мм = – 105,7 Н·м;

Му4 = 0 Му3 = – F_м ·LМ = – 342 ·85 = –29071 Н·мм = – 29,1 Н·м;

3. Строим эпюру крутящих моментов, Н·м

Мк = Мz = F_t1 = 934,6 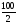= 46730 Н·мм = 46,7 Н·м

4. Суммарные реакции:

RA = =

RB = =

5. Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях, Н·м

М2 = =

М3 = М_У3 = 29,1 Н·м

Рис.1 Ведущий вал

2. Ведомый вал

Дано:

Ft2 = 1700,95 H;

Fr2 = 612,34 H;

Fa2 = 934,6 H;

Fр.п. =

LБ = 156 мм; d2 = 400 мм

LОП = 110 мм;

На рис. 2 составляем расчетную схему вала, проставляем все действующие на вал силы и определяем реакции опор:

2. Вертикальная плоскость

а) определяем опорные реакции

∑ М7 = 0 – Fr2 · + RСУ ·LБ – F_а2 + F_оп ·LОП = 0

RСУ =

∑ М5 = 0 Fr2 · – RDУ ·LБ – F_а2 + F_оп ·(LБ + LОП) = 0

RDУ =

Проверка: RCУ + RDУ – Fr2 – F_оп = 965 + 412 – 612,34 – 764,8 = 0

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 5…8, Нм

Мх5 = 0; Мх6 = RCУ · = 965 · = 75270 Н·мм = 75,3 Н·м;

Мх8 = 0 Му7 = – F_оп ·LОП = – 764,8 ·110 = – 84128 Н·мм = – 84,1 Н·м;

Мх6 = – F_оп ·( LОП + ) + RDУ · = – 764,8 ·(110+78) + 412 · =

= –111646Н·мм = – 111,62 Н·м;

2. Горизонтальная плоскость

а) определяем опорные реакции

∑ М7 = 0 – Ft2 · + RCX ·LБ = 0

RCХ =

∑ М5 = 0 Ft2 · – RDX ·LБ = 0

RDХ = RCХ = 850,5Н

б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 5…7, Нм

Му5 = 0 Му6 = RСХ ·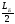 = 850,5· = 66339Н·мм = 66,3Н·м;

Му7 = 0

3. Строим эпюру крутящих моментов, Н·м

Мк = Мz = F_t2 = 1700,95 = 340190 Н·мм = 340,2 Н·м

4. Суммарные реакции:

RС = =

RD = =

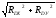5. Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях, Н·м

М6 = =

М7 = М_У7 = 84,1 Н·м

Рис. 2 Ведомый вал

8